книги / Оксидные композиционные материалы

Φ(r )= max{(σ1 (rr)−σ+ )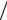σ+,(σ3 (rr)−σ− ) / σ−},

χ( p) (rr)= 1, если r Vp ,

0, если r Vp ,

Cijkl(1) , если Ф(rr)< 0,

Cijkl(2) = 0, Cijkl(1) (σ% (rr))= Kδijδkl , еслиФ(rr)> 0, I1 (σ% (rr))< 0, (50)

0, еслиФ(rr)> 0, I1 (σ% (rr))> 0.

В вышеприведенной системе приняты следующие обозна-

жений; K – объемный модуль.

Индикаторные функции χ( p) (rr) в краевой задаче полно-

стью определяются геометрией моделируемой структуры. Граничные условия:

Система уравнений (50)–(52) не является линейной, поскольку связь между напряжениями и деформациями зависит от уровня и вида напряженного состояния. При удовлетворении критерию прочности, в качестве которого выбран критерий максимальных главных напряжений, зависимость σ–ε является

81

упругой. В противном случае рассматривается два возможных варианта: в области возможного гидростатического сжатия первый инвариант тензора напряжений меньше нуля

(I1 (σ% (rr))< 0), материал работает по типу «песка», т.е. имеет единственную упругую компоненту – объемный модуль упругости, в области гидростатического растяжения (I1 (σ% (rr))> 0) об-

разуется полость. При этом в процессе нагружения возможно образование областей, работающих по типу «песка» вместо полостей, и наоборот.

Эффективные упругие характеристики решетчатой конструкции определялись после вычисления и осреднения по центральной ячейке искомых полей микроструктурных напряжений σ%(rr) и деформаций ε%(r ) по следующим формулам [78]:

ν* = ν E* / E*,

G = σ12* / ε12* ,

где

k * = (σ11* + σ*22 )/ (2(ε11* +ε*22 )), m* = (σ11* −σ*22 )/ (2(ε11* −ε*22 )),

ψ =1+ k *ν*2 / E .

Здесь значком m отмечены характеристики материала стенки решетки.

82

Эффективный критерий прочности, выбранный также в виде критерия максимальных напряжений, определялся с помощью расчета траекторий макронагружения вида

где Sij0 – начальная точка траектории; α – шаг увеличения на-

грузки.

Точка траектории m, в которой начинался лавинообразный процесс разрушения конструкции, считалась конечной и равнялась при соответствующем виде траектории пределам макро-

скопической прочности каркаса σ*− и σ*+ .

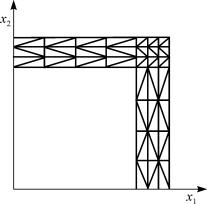
Краевая задача решается с помощью ЭВМ. Рассматриваемая область разделяется на ряд участков, триангуляция которых осуществляется по алгоритму, предложенному С.Э. Уманским [85], примерная картина сетки на одном из участков показана на рис. 22.

Составленный пакет программ позволяет проводить автоматическую дискретизацию при произвольном коэффициенте объемного заполнения решетки. При этом сгущение сетки предусматривается в центральной ячейке, а наибольшее разряжение – в угловых ячейках. Получаемая система линейных уравнений реша-

ется методом Холецкого [86]. Матрица жесткости хранится в профильном формате по схеме Дженнигса [86], что обеспечивает значительную экономию памяти по сравнению с обычной ленточной формой хранения. Минимизация профиля проводилась по двум алгоритмам: обратное упорядочение Катхилла– Макки [86] и упорядочение вдоль координатной линии. Уста-

83

новлено, что для используемой схемы дискретизации второй алгоритм приводит к несколько меньшей величине профиля матрицы жесткости. Для построения центральной периодической или стохастической ячейки, анализа и осреднения полей напряжений и деформаций был разработан специальный блок программ. В нем, в частности, предусматривалось вычисление лишь той части площади элемента, которая принадлежала центральной ячейке, в случае пересечения элемента ее границами погрешность набора площади ячейки составляла порядка 0,02 %.

С целью устранения вырожденности матрицы жесткости при решении поставленной задачи расчетная схема дополнялась фиктивными стержневыми элементами, один узел которых принадлежал границе Г, а второй жестко крепился. Эта процедура равносильна добавлению к соответствующим диагональным элементам матрицы жесткости некоторой произвольной величины (жесткого стержня), ее значение подбиралось минимально достаточным для устранения особенности матрицы жесткости. Влияние стержневых элементов на НДС в центральной ячейке компенсировалось накладываемыми граничными условиями, определяемыми выражением (52). Предложенный прием может оказаться полезным и при решении других кинематически неопределимых задач с граничными условиями в напряжениях с использованием традиционной схемы МКЭ. В отличие, например, от метода, предложенного в работе [87], в данном случае не требуется расширения системы уравнений, а использование тензора корректировки граничных условий позволяет компенсировать влияние дополнительных элементов на НДС в большей части исследуемой области.

Учет нелинейности системы уравнений (50)–(52) за счет возможного накопления в ней поврежденных или разрушенных зон осуществляется с помощью итерационной процедуры по методу начальных напряжений [88]. В этом случае в соотношения (50)–(52) вводится дополнительный тензор начальных напряже-

ний σ% 0 (rr), корректирующий поле напряжений σ% y (rr), получаемое из чисто упругого решения для соответствия его истинному полю напряжений σ% (rr) структуры с разрушением:

84

Уравнение (55) можно переписать с использованием обобщенного закона Гука:

При этом уравнение (56) в отличие от физических соотношений системы (50) содержит постоянный тензор C%(rr), соот-

ветствующий упругому неповрежденному материалу решетки, поэтому используемая итерационная процедура носит еще название метода упругих решений [89].

Смысл начальных напряжений заключается в занулении результирующих напряжений в элементах, разрушенных по типу «полость», и в создании равномерного гидростатического сжа-

тия с давлением P = I1 (σ%,(rr))/ 3 в элементах, разрушенных по

типу «песок».

Аналогичным образом проводится линеаризация уравнения (52), позволяющая определить требуемые граничные условия для области Ω, соответствующие задаваемому макронапряженному состоянию Sij учетом зон структурного разрушения. Уравнение (52) записывается в виде

где A% – постоянный тензор вычисления граничных условий для упругой задачи; S%0 (S%) – тензор осредненных начальных на-

пряжений, зависящий от кинетики структурного разрушения. Общая ускоренная итерационная процедура для решения нелинейной краевой задачи имеет следующую последовательность:

1. Решается упругая задача методом локального приближе-

ния. Требуемые компоненты тензора A% , соответствующие упругой неповрежденной структуре, находятся из решения последовательности дополнительных задач на растяжение вдоль координатных осей и сдвиг [78]. Зависимость между макронапряжениями и граничными условиями имеет вид

85

3. Решается краевая задача для области Ω c граничными условиями σˆ = σˆ (1) и находится поле напряжении σ(1) (rr) в цен-

тральной ячейке.

4. Проводится проверка выполнения условия прочности. В случае отсутствия разрушения Sij(1) = Sij и решение зада-

чи в ячейке ωΣ является искомым. В противном случае произ-

водится корректировка поля напряжения для учета области разрушения по условиям системы (53). При этом

где σ% 0 (1) (rr) – корректирующее поле начальных напряжений на

i-й итерации.

5. Решается дополнительная краевая задача с нулевыми граничными условиями σˆ = 0 и полем начальных напряжений

σ% 0 (1) (rr). Определяются осредненные напряжения по централь-

ной ячейке S 0ij (1) , возникающие от корректирующего поля и находится разность

6. Находится второе приближение для граничных условий σ% (2) из условия

Далее вновь решается краевая задача для области Ω с найденными во втором приближении σˆ ij(2) на границе Г, определя-

86

ется поле σˆ (2) (rr) в центральной ячейке, проводится проверка выполнения условий прочности и корректировка в случае необходимости поля начальных напряжений σ% 0(1) (rr). Потом уточ-

няется разность макронапряжений (61), находится третье приближение для граничных условий (62) и т.д.

Итерационный процесс продолжается до достижения необходимой точности

σ0(m) −σ0(m−1)

σ(m)

III < γ1, (63)

I

σ0(m) −σ0(m−1)

σ(m) I < γ2 ,

I

где соответствующие нормы матриц имеют вид

Проверка пакета программ проводилась на тестовых задачах для композиционных материалов. Различие эффективных упругих характеристик материалов и коэффициентов концентрации напряжений, полученных аналитическими методами [90, 91] и с помощью разработанного комплекса программ, не превышало 5 %.

6.2.2. Численное прогнозирование разрушения сотовых конструкций на основе диоксида титана

Как отмечалось, в процессе эксплуатации блочных сотовых носителей катализаторов возможна деградация механических свойств материала каркаса и изменения его регулярной геометрии, связанные с физико-химическими процессами вследствие воздействия движущегося потока химически агрессивной среды. С феноменологической точки зрения эти процессы могут быть

87

интерпретированы как изменения прочностных и упругих свойств материала каркаса, а также объемной доли пор макроструктуры, определяемые сроком эксплуатации изделия. Для исследования их влияния на кинетику развития повреждаемости блочных сотовых носителей катализаторов на основе керамики были проведены расчеты, позволяющие проанализировать изменение эффективных прочностных свойств и характера разрушения конструкции в целом при различных свойствах материала каркаса и различной пористости макроструктуры. Кроме того, поскольку развитие повреждаемости катализаторов при механическом нагружении в значительной степени определяется также конструктивными особенностями формирования блоков (см. рис. 18), данное обстоятельство предопределило необходимость схемы нагружения на процессы разрушения конструкции в целом. Численное исследование предполагало анализ изменения напряженно-деформированного состояния в материале каркаса в процессе повышения нагрузки до предельных прочностных значений, расчет упругих и прочностных свойств конструкции в целом, а также описание механизма и кинетики разрушения конструкции при нарушении критериального условия прочности.

Влияние армирования на эффективные упругие прочностные свойства

решетчатой конструкции при различной объемной доле макропор

Объектом исследования являлась квадратная решетчатая конструкция из керамического материала. Упругие характеристики неармированной керамики и керамики, упрочненной дискретными стекловолокнами, приведены в подразд. 6.1. В последнем случае принималось, что объемная доля стекловолокон Vf = 0,3. Прочностные свойства армированной керамики в расчетах принималась по результатам экспериментов σ+ = 4 МПа, σ– = 6 МПа (для неармированного диоксида титана σ+ = 2 МПа,

σ– = 3 МПа).

Рассматривалось три варианта геометрии решетчатой конструкции с объемной долей макропор, равной 0,5; 0,6 и 0,7. За-

88

даваемые траектории простого нагружения соответствуют условиям поперечного растяжения, сжатия, сдвига.

Для расчета напряженно-деформированного состояния и оценки прочности исследуемой конструкции использовался программный комплекс решения краевых задач микромеханики неоднородных сред.

В целях обеспечения корректности процесса осреднения по ячейке периодичности решетчатой конструкции в настоящих исследованиях предполагалось, что макропоры заполнены фиктивным податливым материалом с жесткостями Е = –1 МПа,

ν = 0,1, G = 0,5 МПа.

Указанное допущение практически не влияет на характер полей напряжений и деформаций в стенках решетчатого каркаса, но позволяет провести осреднение деформаций и напряжений по всей площади ячейки, включая и пору, в рамках разработанного алгоритма. Картина триангуляции четверти центральной ячейки показана на рис. 22.

Полученные эффективные упругие характеристики решетчатой конструкции представлены в табл. 12, где в числителе приведены данные для обычной керамики, в знаменателе – для армированной.

Таблица 12

Эффективные упругие константы решетчатой структуры диоксида титана

89

Из табл. 12 видно, что наибольшей степени зависит от объемной доли макропор модуль сдвига и модуль Юнга в поперечной плоскости (G и F).

Коэффициент Пуассона ν|| в исследованном диапазоне вариаций объемной доли пор практически, не изменяется. Армирование керамики дискретным стекловолокном (Vf = 0,3) позволяет увеличить жесткостные характеристики решетчатой структуры E||, E , G приблизительно в 2,8 раза, коэффициенты Пуассона – ν||, ν , ν|| при этом увеличиваются только на ~ 10 %.

Расчеты по траекториям растяжения, сжатия и сдвига проводились от начальных точек с координатами в пространстве напряжений

Sij0 {S110 ; S220 ; S120 }: {0,25; 0; 0}, {0,5; 0; 0}, {0; 0; 0,25}.

Следующие точки определялись в соответствии с формулами

вобласти мелкого шага β на участке разрушения до точки m.

Врасчетах принималось α = 1, β = 0,25 .

Расчеты траекторий свидетельствуют о лавинообразном характере разрушения с момента зарождения первого дефекта. Характер разрушения соответствует условиям нагружения: при растяжении разрушение наступает вследствие превышения растягивающими напряжениями предельной нагрузки (для армированного диоксида титана σ+ = 4 МПа; для неармированного σ+ = = 2 МПа), при сжатии – вследствие превышения напряжениями сжатия предельной нагрузки (σ– = 6 МПа, σ– = 3 МПа соответственно для армированного и неармированного диоксида титана).

При сдвиге в первую очередь не выполнялся критерий максимальных растягивающих напряжений. Наиболее слабая

90