
книги / Принципы и практика решения задач по общей физике. Оптика. Квантовая физика
.pdf
(это не совсем «нормальное» условие, так как обычно плотность воздуха убывает с высотой). Для определения условий выполнения соотношения (1) воспользуемся уравнением Менделеева–Клапейрона в форме ρ =µP / (RT ) , где P – давление; µ – молярная масса возду-
ха; R – универсальная газовая постоянная; T – температура. Из него находим
ρ1 ddhρ = P1 dPdh −T1 dTdh .
При механическом равновесии воздуха dP = −ρgdh , где g – ускорение свободного падения. Отсюда получаем
dTdh < −µRg ≈ −0,025 К/м.
Такое распределение температур конвективно неустойчиво (вспомним закон Архимеда). Для конвективной устойчивости, как показывают расчеты, необходимо, чтобы градиент температуры не превышал примерно 1 °С на каждые 100 м высоты.
1.1.4. Свет в зеркальном ящике. Светящаяся точка A находится между тремя зеркалами (рис. 1.7, а). Зеркала 1 и 3 параллельны друг другу, а зеркало 2 им перпендикулярно. Построить луч, который после последовательного отражения в зеркалах вернется в исходную точку.
|
|
|
|
|
|
|
|
а |
б |
Рис. 1.7
11
Конечно, опираясь на закон отражения, можно путем последовательных приближений построить требуемый ход луча, но это слишком длинный путь. Нужна более радикальная идея. Для этого учтем, что выходящие из точки A лучи будут падать на зеркала и отражаться от них расходящимися пучками, давая всякий раз на своем продолжении мнимые изображения. В нашем случае точка A даст в зеркалах три мнимых изображения, расположенных симметрично точке A относительно зеркал. Каждое изображение будет источником для этих зеркал и даст в свою очередь новые изображения. Нетрудно понять, что в данной задаче число изображений точки A будет бесконечным. Поэтому будем строить их последовательно одно за другим до тех пор, пока не выполнится условие задачи.
Точка A в первом зеркале даст изображение A1 (рис. 1.7, б), которое будет предметом для зеркала 2. При этом точки A и A1 будут расположены симметрично относительно зеркала 1. Изображение A2 в зеркале 2 будет расположено симметрично точке A1 относительно зеркала 2. Изображение A3 точки A2 в зеркале 3 будет расположено симметрично точке A2 относительно зеркала 3. Поскольку изображение A1 получается на продолжении лучей, отраженных зеркалом 1, изображение A2 – лучей, отраженных зеркалом 2, изображение A3 – лучей, отраженных зеркалом 3, то на изображении A3 сле-
дует остановиться (по условию задачи луч должен последовательно отразиться от всех зеркал по одному разу и вернуться в точку A ).
Прямая, соединяющая точки A3 и A , определит направление
луча, отраженного зеркалом 3 в направлении точки A . В точку D пересечения этой прямой с зеркалом 3 луч падает так, как будто он выходит из точки A2 . Поэтому прямая A2 D определит направление луча, отраженного зеркалом 2 в направлении точки D. Аналогично, в точку C пересечения этой прямой с зеркалом 2 луч падает так, как будто он выходит из точки A1 . Тогда прямая A1C определит направление луча, отраженного зеркалом 1 в направлении точки C. И для
12

завершения хода луча осталось лишь направить луч из точки A в точку B пересечения прямой A1C с зеркалом 1. Из геометрических соображений нетрудно убедиться, что в точках B, C и D выполняется закон отражения (равенство углов падения и отражения).
Решите самостоятельно следующую задачу. Построить луч, ко-
торый, выйдя из точки A |
зеркального прямоугольного ящика |
|
(рис. 1.8, а), пройдет через точку B, |
отразившись по одному разу от |
|
всех четырех стенок. Точки |
A и |
B лежат в плоскости рисунка. |
(Ответ: см. рис. 1.8, б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
|
|
|
Рис. 1.8 |
|
|
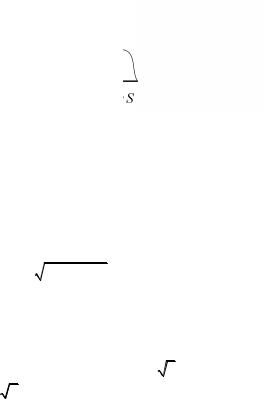
1.1.5. Двухгранное зеркало. Сколько изображений даст светя- |
||
щаяся точка S, |
находящаяся на биссектрисе двухгранного зеркала |
||
с углом раствора α = 2π/ n, где n – целое число, большее единицы? Обратимся к рис. 1.9. На нем обозначено: 1 и 2 – зеркала, S – источник света, S1(n) – n -е отражение в зеркале 1, S2(n) – n -е отра-
жение в зеркале 2. Так как изображения расположены симметрично относительно соответствующего зеркала, то, очевидно, все изображения располагаются на окружности радиуса OS и сдвинуты относительно друг друга на один и тот же угол α. Понятно, что процесс построения новых изображений закончится, как только изображе-
13

ние S1(i) совместится с изображением S2(i) , т.е. изображения, создавае-
мые каждым зеркалом, повернутся на π. Отсюда сразу находим, что число всех изображений будет в два раза больше отношения π/ α. И если еще учесть, что два последних изображения совмещены, то полное число изображений
N = 2 |
π |
−1 = 2 |
πn |
−1 = n −1. |
|
α |
2π |
||||
Рис. 1.9 |
|
|
1.1.6. Смещение фокуса фотоаппарата. Как сместится фокус фотоаппарата, если между объективом и фотопленкой перпендикулярно оптической оси поместить плоскопараллельную стеклянную пластинку толщиной d с показателем преломления n ? Считать объектив сильно задиафрагмированным.
|
Так как объектив сильно задиа- |
|
|
фрагмирован, то следует рассматри- |
|
|
вать только параксиальные лучи, |
|
|
идущие под малыми углами к опти- |
|
|
ческой оси. Рассмотрим ход двух лу- |
|
|
чей – один совпадает с оптической |
|
|
осью, другой идет к ней под малым |
|
|
углом α (рис. 1.10). Для упрощения |
|
Рис. 1.10 |
расчетов в качестве второго луча вы- |
|
берем такой луч, который после пре- |
||
|
ломления на передней поверхности стеклянной пластинки пересечет оптическую ось на задней поверхности пластинки. Из рис. 1.10 видно, что фокус фотоаппарата отодвинется на расстояние SS′ = =OS −OS′. И так как
14
OS |
= tg α |
≈ sin α = n, |
OS′ |
tgβ |
sin β |
то смещение фокуса составит |
|
|
∆ = d − d |
= d n −1 . |
|
|
n |
n |
Если рассматривать точку S |
как предмет, а точку S′ – как его |
|
изображение, то видно, что кажущаяся толщина стеклянной пластинки в параксиальных лучах, перпендикулярных поверхности пластинки, меньше истинной в n раз. На этом основан один из методов определения показателя преломления стекла. Плоская стеклянная пластинка рассматривается в микроскоп. Сначала микроскоп устанавливают для наблюдения верхней поверхности пластинки, а затем тубус микроскопа смещают вниз до тех пор, пока не будет отчетливо видна нижняя поверхность пластинки (для удобства наблюдения на поверхностях пластинки наносятся метки). И по отношению истинной толщины пластинки к смещению тубуса определяют показатель преломления.
1.1.7. Камень в воде. На краю бассейна глубиной H стоит человек и наблюдает камень, лежащий на дне. На каком расстоянии от поверхности воды h видно изображение камня, если луч зрения составляет с нормалью к поверхности воды угол α ? Показатель преломления воды n.
Если бы человек рассматривал камень, находящийся на одной вертикали с его глазами, то, очевидно, кажущаяся глубина камня была бы меньше истинной ровно в n раз (см. предыдущую задачу 1.1.6). Теперь же необходимо построить ход двух лучей, выходящих из воды под близкими углами α и α+δα, и затем на их про-
должении найти изображения камня S′. Сам же камень находится в точке S (рис. 1.11). Из рис. 1.11 следуют равенства
l1 = H tgβ, l2 = H tg (β+δβ).
15

l1 −h tg α =l2 −h tg (α+δα).
|
|
|
|
Из них находим |
|
|
|
|
|
|
|||
|
|
|
|
|
h = H |
tg (β+δβ) −tgβ |
|
||||||
|
|
|
|
|
|
. |
(1) |
||||||
|
|
|
|
|
tg (α+δα) −tg α |
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Так как углы δα и δβ малы по |
|||||||||
|
|
|
сравнению с α и β, то используя раз- |
||||||||||
|
|
|
ложение тангенса в ряд |
|
|
|
|
|
|
||||
|
|
|
|
|
tg (x +δx) ≈ tgx + |
|
1 |
|
δx, |
|
|||
|
Рис. 1.11 |
|
|
|
|
|
|||||||
|
|
|
2 |
x |
|
||||||||
|
|
|
|
|
|
|
|
cos |
|
|
|
||
вместо (1) получаем |
|
|
|
|
|
|
|
|
|
|
|
||
|
h = H |
cos2 |
α δβ |
. |
|
|
|
|
|
|
(2) |
||
|
cos2 |
β δα |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Воспользуемся теперь |
законом преломления |
nsinβ = sin α |
||||||||||
и найдем его дифференциал: |
ncosβ δβ = cosα δα. Подставляя най- |
||||||||||||
денное отсюда отношение δβ к δα в (2), приходим к соотношению
h = |
H cosα 3 |
|
|
. |
|
|
n cosβ |
|
И если выразить теперь угол β через α, воспользовавшись законом преломления, то для h получаем
h = n |
2 |
|
cos α |
|
|
3 |
|
|
|
|
. |
||
|
n2 −sin2 |
|
||||
|
|
|
α |
|
||
Горизонтальное же смещение камня составляет
l = H tgβ−h tg α = H |
sin α |
−h tg α. |
n2 −sin2 α |
16
PNRPU
1.1.8. Стеклянный кубик. Можно ли увидеть что-нибудь через две смежные грани стеклянного кубика? Показатель преломления стекла n =1,5.
Для того чтобы увидеть свет от источника S (рис. 1.12) через две смежные грани кубика, необходимо, чтобы луч, вошедший через одну грань, не испытал полного внутреннего отражения на другой грани. Чтобы убедиться, при каких условиях может произойти полное внутреннее отражение, построим ход какого-либо луча и найдем связь угла падения α и угла, под которым
луч может выйти в воздух. Применим последовательно закон преломления к двум граням кубика
sin α |
= n, |
cosβ |
= |
1 . |
sinβ |
|
sin γ |
|
n |
Из этих равенств следует
sin γ = n2 −sin2 α .
И так как sin γ не может быть больше единицы, для показателя пре-
ломления получаем неравенство n2 ≤1+sin2 α. Откуда видно, что предельное значение показателя преломления, при котором свет мо-
жет выйти через две смежные грани кубика, равно 2. Для стекла же n =1,5, что явно больше 2, т.е. увидеть что-либо через две смежные грани стеклянного кубика невозможно. Если же под основание кубика ввести воду (n =1,33), то теперь появляется возможность вы-
хода света через другую грань.
1.1.9. Стеклянный капилляр. Если смотреть на капиллярную трубку сбоку, то видимый внутренний радиус будет равен r′. Каков истинный внутренний радиус?
Для определения соотношения истинного внутреннего радиуса капилляра и наблюдаемого достаточно построить ход двух лучей,
17
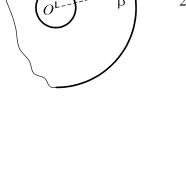
|
исходящих от какой-либо точки |
||
|
|||
|
внутренней |
поверхности капилля- |
|
|
ра S и выходящих через его внеш- |
||
|
нюю поверхность. Один из лучей |
||
|
очевиден – это луч 1, идущий вдоль |
||
|
радиуса капилляра (рис. 1.13). Если |
||
|
в качестве второго взять луч, идущий |
||
|
под небольшим углом к первому, то |
||
|
мы столкнемся с довольно утоми- |
||
|
тельными тригонометрическими вы- |
||
Рис. 1.13 |
кладками по определению точки пе- |
||
ресечения |
его продолжения с пер- |
||
|
|||
вым. Поэтому возьмем луч, исходящий перпендикулярно первому. Так как истинный внутренний радиус капилляра r = OS является малой величиной, то углы падения и преломления на внешней поверхности капилляра α и β также малы, т.е. их тангенсы примерно равны их синусам или самим углам. Тогда из рис. 1.13 следует
OS = r ≈ CS β, OS′ = r′−r ≈ CS (α−β).
После деления этих равенств получаем
|
r′−r |
= |
α−β. |
|
|
|
|||
|
r |
|
β |
|
Если теперь учесть закон преломления α/ β ≈ n, то окончатель- |
||||
но находим |
|
|
||
|
r = |
r′ |
, |
|
|
|
|||
|
|
|
n |
|
т.е. происходит зрительное увеличение внутреннего радиуса капилляра, если его рассматривать сбоку.
1.1.10. Световод. Каким должен быть внешний радиус R изгиба световода, сделанного из прозрачного материала с показателем преломления n, чтобы при диаметре световода d, свет, вошедший в
18

световод перпендикулярно плоскости его поперечного сечения, распространялся, не выходя через боковую поверхность наружу?
Понятно, что наивысшие шансы выйти из световода имеет луч, входящий в него у внутреннего радиуса (самый малый угол падения). И если этот луч не выйдет при первом касании внешнего радиуса световода, то при дальнейших отражениях угол падения только увеличивается (рис. 1.14), что сдела-
ет невозможным выход луча через внешнюю поверхность. Таким образом, для достижения полного внутреннего отражения угол α должен удовлетворять условию
sin α = 1n .
Кроме того, из рис. 1.14 видно, что
sin α = R R−d .
Из этих двух равенств находим
R= d nn−1.
1.1.11.Угловая апертура световода. Прямолинейный длинный
цилиндрический световод |
изготовлен из прозрачного материала |
с показателем преломления |
n. На одном из торцов световода нахо- |
дится точечный источник освещения. Найти угол β между крайними
лучами, вышедшими через противоположный торец (угловая апертура пучка света).
Лучи от точечного источника света будут падать на боковую цилиндрическую поверхность световода под разными углами в интервале от 0 до π/ 2. Часть из них преломится на границе с воздухом
19
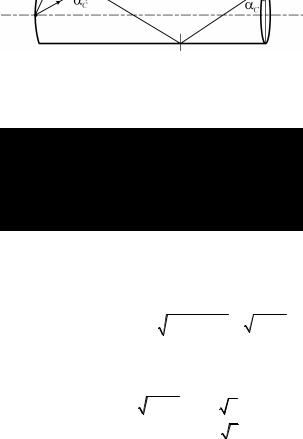
и выйдет из световода наружу (рис. 1.15), а часть испытает полное внутреннее отражение и будет продвигаться через световод. Очевидно, что отраженные один раз лучи больше нигде из световода не выйдут и доберутся до противоположного торца. Угол, под которым эти лучи выйдут через торец, и есть половина угловой апертуры пучка. Запишем для них закон преломления (нормаль перпендикулярна торцу световода):
sin (β/ 2) = n, cosαC
где αC – предельный угол полного внутреннего отражения от боковой поверхности световода. Его значение
αC = arcsin (1/ n).
Рис. 1.15
Таким образом, имеем
sin (β/ 2) = n cos αC = n 1−sin2 αC = n2 −1.
Отсюда находим угловую апертуру пучка света, проходящего через световод:
|
n |
2 |
−1, n < |
2, |
2arcsin |
|
|||
β = |
|
|
n ≥ |
|
π, |
|
|
2. |
|
|
|
|
|
|
20
