Вероятностный смысл математического ожидания

Пусть проведено nиспытаний, в которых случайная величинаХприняла раз значение , раз значение , … , раз – , Тогда сумма всех значений, принятыхХравна . Найдем среднее арифметическоевсех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытанийn:

где - относительная частота (частость).

Допустим, что число испытаний достаточно велико, тогда и

Таким образом, математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства м(х)

1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С) = С, С = const.

С имеет одно значение, равноеС, с вероятностьюp = 1,М(С)=С ^.1 = С.

Определим произведение постоянной СнаХкак дискретную случайную величину, возможные значения которой равны произведениямСна возможные значенияХ. Вероятностьравна вероятностямХ. Например, еслиимеет вероятность, тоимеет также вероятность.

2. М(СХ) = С ^. М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величинаX задана законом распределения:

		…
		…

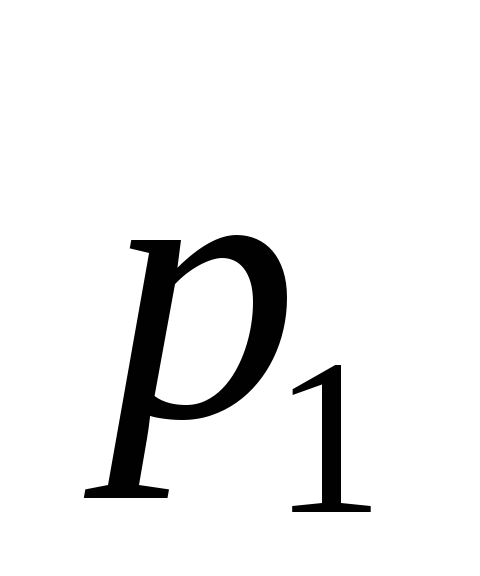
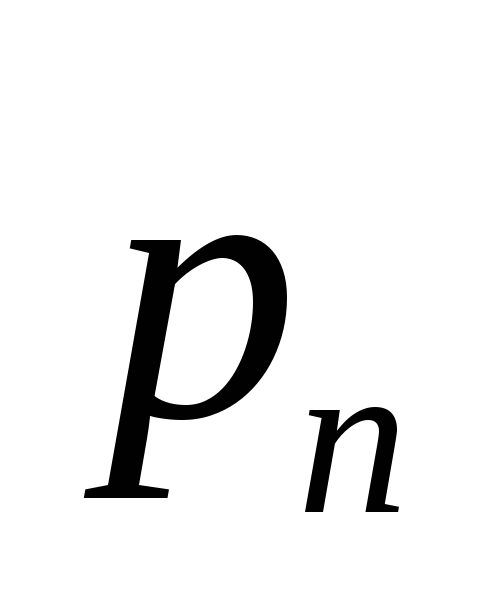
Тогда имеет закон распределения:

		…
		…

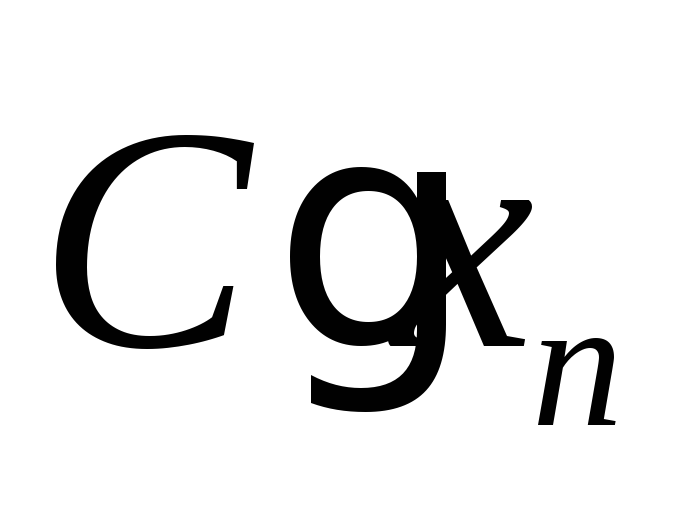
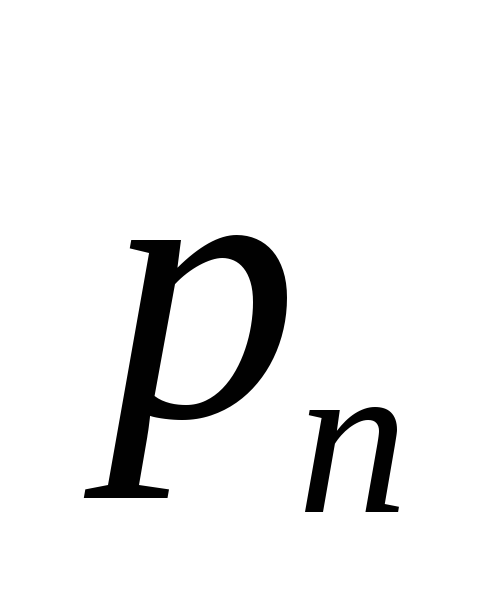
Случайные величины XиYназываютнезависимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая.

Произведение – случайная величинаXY, возможные значения которой равны произведениям каждого возможного значенияХна каждое возможное значениеY. ВероятностиXY равны произведению соответствующих вероятностейXиY.

3. , гдеX,Y– независимые дискретные случайные величины.

Пусть законы распределения вероятностей этих величин:

Составим значения, которые могут принимать Закон распределения:

4. M(X+Y) = M(X) + M(Y).

Возможные значения случайной величины X+Yравна сумме возможных значенийXиY, а вероятностьX+Yравна произведению вероятностей слагаемых.

Теорема.М(Х) числа появлений событийАвnнезависимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытанииp.

Иначе, М(Х) биноминального распределения равно.

22.5. Дисперсия случайной дискретной величины и ее свойства

Легко указать случайные величины, имеющие одинаковые значения математических ожиданий, но различные возможные значения, например:

	–0,1	0,1				–10	10
	0,5	0,5				0,5	0,5

Химеет возможные значения, близкие к математическому ожиданию, аY– далекие отМ(Y), таким образом,М(Х) полностью не характеризуетХ. Надо охарактеризовать отклонение случайной величины отM(X): отклонение – это величинаX – M(X).

Теорема. Математическое ожидание отклонения равно нулю.

Действительно, , поэтому для оценки отклонения берутквадратотклонения.

Дисперсией (рассеянием)дискретных случайных величин называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:.

Получаем:

Пример.Найтислучайной величины:

	1	2	5
	0,3	0,5	0,2

M(X) = 1^.0,3 + 2^.0,5 + 5^.0,2 = 2,3. Найдем все возможные значения квадрата отклонения:= (1 – 2,3)²= 1,69;= (2 – 2,3)²= 0,09;

Напишем закон распределения квадрата отклонения:

	1,69	0,09	7,29
	0,3	0,5	0,2

Тогда (по определению): = 1,69^.0,3 + 0,09^.0,5 + 7,29^.0,2 = 2,01.

Удобнее: .

Доказательство:

.

Вычислим дисперсию в предыдущем примере по доказанной формуле. Составим закон распределения :

	1	4	25
	0,3	0,5	0,2

Тогда = 1^.0,3 + 4^.0,5 + 25^.0,2 = 7,3. Найдем: