
Математика
.docx51 Производные высших порядков
Если
функция
![]() имеет
производную в каждой точке
имеет
производную в каждой точке
![]() своей
области определения, то ее производная
своей
области определения, то ее производная
![]() есть
функция от
есть
функция от
![]() .
Функция
.
Функция
![]() ,
в свою очередь, может иметь производную,
которую называют производной
второго порядка
функции
,
в свою очередь, может иметь производную,
которую называют производной
второго порядка
функции
![]() (или
второй
производной)
и обозначают символом
(или
второй
производной)
и обозначают символом
![]() .
Таким образом
.
Таким образом
![]()
Вычисления производной любого порядка, формула Лейбница
Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение формулы вычисления производной от произведения двух функций, применяется формула Лейбница:
![]()
где
![]() ,
,
![]() -
факториал натурального
числа
-
факториал натурального
числа
![]() .
.
52 Дифференциал функции
Пусть
функция
![]() дифференцируема
в точке
дифференцируема
в точке
![]() ,
то есть приращение этой функции можно
представить в виде суммы двух слагаемых:
линейного относительно
,
то есть приращение этой функции можно
представить в виде суммы двух слагаемых:
линейного относительно
![]() и
нелинейного членов:
и
нелинейного членов:
![]()
где
![]() при
при
![]() .
.
Определение
Дифференциалом
функции
называется линейная относительно
![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как
![]() или
или
![]() .
Таким образом:
.
Таким образом:
![]()
Замечание
Дифференциал функции составляет основную часть ее приращения.
Замечание
Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:
![]()
Замечание
Формулу для дифференциала функции можно записать в виде:
![]()
Отсюда получаем, что
![]()
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.
Геометрический смысл дифференциала
Дифференциал
функции в точке
![]() равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента
равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента
![]() .
.
53 Дифференциалы высших порядков.
Определение 19.2. Дифференциал от дифференциала функции называется ее вторым дифференциалом или дифференциалом второго порядка.
Обозначение: d²y=d(dy).
При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.
Итак, d²y=d(dy)=d(f΄(x)dx)=(f΄(x)dx)΄dx=(f΄(x))΄(dx)²=f΄΄(x)dx². (19.3)
Подобным же образом можно найти третий дифференциал от данной функции:
d³y=d(d²y)=f΄΄΄(x)d³x и дифференциалы более высоких порядков.
Определение 19.3. Дифференциалом n-го порядка называется первый дифференциал от дифференциала (n-1)-го порядка:
dny = d(dn-1y) = (f(n-1)(x)dn-1x)΄ = f(n)(x)dnx. (19.4)
Свойства дифференциалов высших порядков.
-
Производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
. (19.5)
-
Дифференциалы высших порядков не обладают свойством инвариантности.
Покажем это на примере второго дифференциала. Если y=F(φ(x))=F(u), где u=φ(x), то d²y=d(F΄(u)du). Но du=φ΄(x)dx зависит от х, поэтому d²y=d(F΄(u))du+Fu΄(u)d(du)=F΄΄uu(u)(du)²+Fu΄(u)d²u, где d²u=φ΄΄(x)(dx)². Таким образом, форма второго дифференциала изменилась при переходе к аргументу u.
54 Теорема Лагранжа.
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка
a
<
< b,
такая, что
![]()
Доказательство. Рассмотрим некоторую вспомогательную функцию
F(x) = f(x) – yсек АВ
Уравнение секущей АВ можно записать в виде:
![]()
![]()
Т
к.
![]() ,
то
,
то
![]() ,
следовательно
,
следовательно
![]()
Теорема доказана.
Определение.
Выражение
![]() называется
формулой
называется
формулой
Лагранжа или формулой конечных приращений.
Теорема Коши.
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка , a < < b, такая, что
![]() .
.
Доказательство. Рассмотрим вспомогательную функцию
![]() ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка ,
a < < b, такая, что F() = 0. Т.к.
![]() ,
то
,
то
![]()
А
т.к.
![]() ,
то
,
то
![]()
55 Экстремумы функции.
Точку
![]() называют
точкой
максимума
функции y=f(x),
если для всех x
из ее окрестности справедливо неравенство
называют
точкой
максимума
функции y=f(x),
если для всех x
из ее окрестности справедливо неравенство
![]() .
Значение функции в точке максимума
называют максимумом
функции
и обозначают
.
Значение функции в точке максимума
называют максимумом
функции
и обозначают
![]() .
.
Точку
![]() называют
точкой
минимума
функции y=f(x),
если для всех x
из ее окрестности справедливо неравенство
называют
точкой
минимума
функции y=f(x),
если для всех x
из ее окрестности справедливо неравенство
![]() .
Значение функции в точке минимума
называют минимумом
функции
и обозначают
.
Значение функции в точке минимума
называют минимумом
функции
и обозначают
![]() .
.
Под
окрестностью точки
![]() понимают
интервал
понимают
интервал
![]() ,
где
,
где
![]() -
достаточно малое положительное число.
-
достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Достаточные условия экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Пусть
функция y=f(x)
дифференцируема в
![]() -окрестности
точки
-окрестности
точки
![]() ,
а в самой точке
,
а в самой точке
![]() непрерывна.
непрерывна.
Тогда
-
если
 при
при
 и
и
 при
при
 ,
то
,
то
 -
точка максимума;
-
точка максимума;
-
если
 при
при
 и
и
 при
при
 ,
то
,
то
 -
точка минимума.
-
точка минимума.
Другими словами:
-
если в точке
 функция
непрерывна и в ней производная меняет
знак с плюса на минус, то
функция
непрерывна и в ней производная меняет
знак с плюса на минус, то
 -
точка максимума;
-
точка максимума;
-
если в точке
 функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то
функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то
 -
точка минимума.
-
точка минимума.
Второй признак экстремума функции.
Пусть
![]() ,
,
-
если
 ,
то
,
то
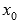 -
точка минимума;
-
точка минимума;
-
если
 ,
то
,
то
 -
точка максимума.
-
точка максимума.
Как
видите, этот признак экстремума функции
требует существования производной как
минимум до второго порядка в точке
![]() .
.
Третье достаточное условие экстремума функции.
Пусть
функция y=f(x)
имеет производные до n-ого
порядка в
![]() -окрестности
точки
-окрестности
точки
![]() и
производные до n+1-ого
порядка в самой точке
и
производные до n+1-ого
порядка в самой точке
![]() .
Пусть
.
Пусть
![]() и
и
![]() .
.
Тогда,
-
если n – четное, то
 -
точка перегиба;
-
точка перегиба;
-
если n – нечетное, то
 -
точка экстремума, причем
-
точка экстремума, причем
-
если
 ,
то
,
то
 -
точка минимума;
-
точка минимума;
-
если
 ,
то
,
то
 -
точка максимума.
-
точка максимума.
-
56 Выпуклость, вогнутость функции, точка перегиба.
Определение.
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Определение.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
Посмотрите на чертеж, иллюстрирующий эти определения.

Определение.
Точка
![]() называется
точкой
перегиба графика функции
y=f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
называется
точкой
перегиба графика функции
y=f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
![]() ,
в пределах которой слева и справа от
точки М
график функции имеет разные направления
выпуклости.
,
в пределах которой слева и справа от
точки М
график функции имеет разные направления
выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

57
Исследование
функции на экстремум.
Производная
f ‘(x)
является точечной характеристикой
зависимой переменной величины y
= f(x) , но может
быть эффективно использована для общего
анализа функции.
Монотонность.
Опр.
Функция
f(x)
на интервале [a,b]
монотонно
возрастает,
если при любых х
> x0
имеем f(x)
> f(x0)
и монотонно
убывает,
если f(x) <
f(x0)
Теорема:
Необходимым
и достаточным условием возрастания
(убывания) функция f(x)
на интервале [a,b]
служит
неравенство
f
‘(x) > 0 ( f
‘(x) < 0 ) для
x
![]() [a,b].
( 25 )
Док
– во необходимости:
Для возрастающей функции справедливо
неравенство (f(x)
- f(x0))/
(x – x0)
> 0 . Переход
к пределу дает производную
lim
( f(x) - f(x0)
)/ (x – x0)
= f ‘(x ) > 0
x
[a,b].
( 25 )
Док
– во необходимости:
Для возрастающей функции справедливо
неравенство (f(x)
- f(x0))/
(x – x0)
> 0 . Переход
к пределу дает производную
lim
( f(x) - f(x0)
)/ (x – x0)
= f ‘(x ) > 0
x
![]() x0
Док
– во достаточности: Пусть
х1,
х2
x0
Док
– во достаточности: Пусть
х1,
х2![]() [a,b] и x1
< x2
. Применим
формулу Лагранжа ( 22 ) для [x1,x2]
: f(x2)
– f(x1)
= f ‘(c ) (x2
- x1
). Если f
‘(x) > 0 на
(x1,x2)
, то f
‘(c ) > 0 и
f(x2)
– f(x1)
> 0
f(x2)
> f(x1)
, т.е. f(x)
на (x1,x2)
возрастает.
[a,b] и x1
< x2
. Применим
формулу Лагранжа ( 22 ) для [x1,x2]
: f(x2)
– f(x1)
= f ‘(c ) (x2
- x1
). Если f
‘(x) > 0 на
(x1,x2)
, то f
‘(c ) > 0 и
f(x2)
– f(x1)
> 0
f(x2)
> f(x1)
, т.е. f(x)
на (x1,x2)
возрастает.![]()
![]()
![]()
![]()
