Операции над множествами

Если имеются два (или более) множества, то на основе их можно получить новые множества при помощи операций (отношений) над ними. Геометрически, для наглядного представления, данные отношения можно представить при помощи кругов, которые один из первых использовал для решения задач Г.Лейбниц, затем развил их применение Леонард Эйлер и особенного расцвета достигшие в сочинениях английского логика Джона Венна, поэтому такие схемы иногда называютДиаграммы Эйлера-Венна.

Диаграммы используются в математике, логике, менеджменте, особое применение они нашли в современной логико-математической теории «формальных нейронных сетей».

На Диаграммах Эйлера-Венна универсальное множествоUизображается в виде прямоугольника, его подмножества – в виде кругов (реже прямоугольников), а элементы принадлежащие данным подмножествам в виде точек (см. Рисунок 2).

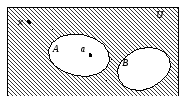
Рисунок 2. Пример диаграммы Эйлера-Венна

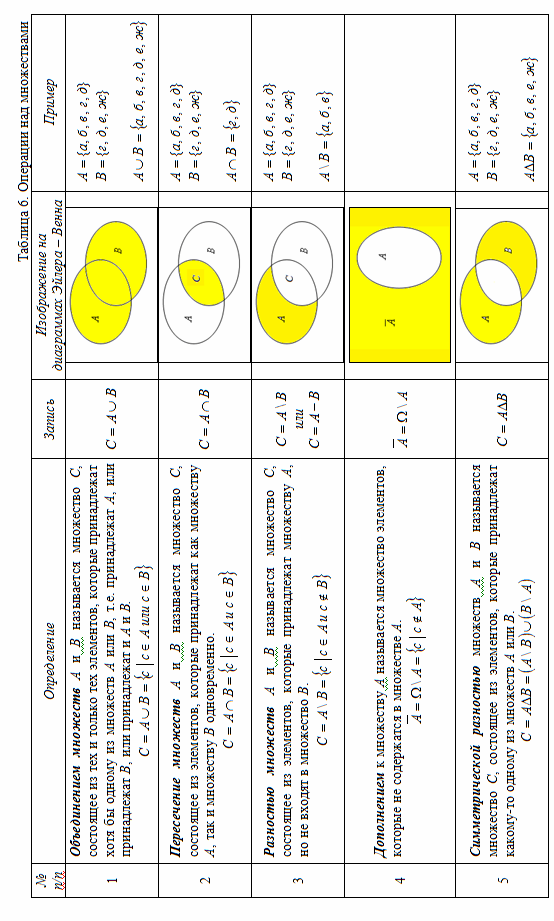
Рассмотрим операции над множествами, некоторые из которых (объединение и пересечение) аналогичны операциям сложения и умножения целых чисел.

Операции пересечениеиобъединениемножеств выполняются для любой пары множеств. Операциядополнениеимеет смысл для тех множеств, когда второе является подмножеством первого.

Следует провести аналогию между логическими операциями и операциями над множествами.

Высказывание	Множество
(конъюнкция)	Пересечение
(дизъюнкция)	Объединение
(импликация)	Разность
(отрицание)	( дополнение)
тавтология	(универсальное множество)
противоречие	Ø (пустое множество)

Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, ,– формулы алгебры множеств.

 Основные законы над множествами

Законы: Закон идемпотентности: a) б) Закон коммутативности: a) б) Закон ассоциативности: a) б) Закон дистрибутивности: a) б) Закон поглощения: a) б) Закон де Моргана: a) б) Закон двойного отрицания: Ø Законы для объединения, пересечения и дополнения: а) ; б); в)Ø =A; г)Ø = Ø; д); е)Ø Законы для разностей: а) ; б) Ø; в) Ø = A;г) Ø Ø; д) Ø

Доказательство каждого из перечисленных законов основано на определении равенства множеств и определений операций над множествами. Чтобы доказать некоторое тождество A=B, нужно доказать, что, во-первых, еслиxА, тоxВи, во-вторых, еслиxВ, тоxА. Докажем один из этих законов:.

Пусть 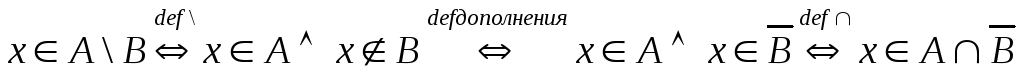¹. Таким образом, мы взяли произвольный элемент изи при помощи равносильных преобразований получили, что он принадлежит, т.е..

И действительно это так, проиллюстрируем это на диаграммах Эйлера-Венна (см. Рисунок 3).

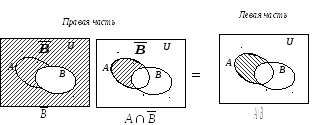
Рисунок 3. Пример иллюстрации равенства множеств на диаграммах Эйлера-Венна

Пример 6.

Пусть А,ВиСпроизвольные множества. Докажите, что(закон дистрибутивности).

Пусть

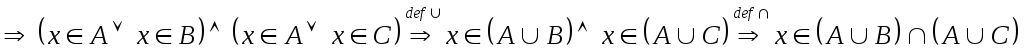, т.е..

Пусть

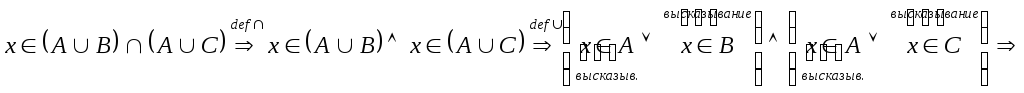
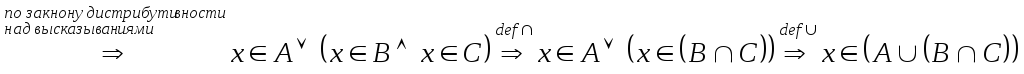, т.е..

Так как и, значит.

Основные законы алгебры множеств можно использовать для доказательства других тождеств.

Пример 7.

Докажите равенство .

Решение.

, что и требовалось доказать.