Методические указания

(номер раздела совпадает с номером задачи в контрольной работе)

Теория вероятностей

1. Непосредственное вычисление вероятностей.

Надо знать: пространство элементарных исходов, формулу классической вероятности и условия ее применения, основные формулы и правила комбинаторики. Геометрические вероятности.

Разделы литературы: [1] гл.1, §1-8; [2] гл.1, §1, 2.

Пример 1. В коробке лежат девять карточек, на которых написаны цифры от 1 до 9. Последовательно наугад вынимают две карточки и кладут их рядом – получают двухзначное число. Найдите вероятность события А – «Первая цифра числа в два раза меньше второй».

Решение.

Все числа (исходы), которые могут быть получены в результате такого испытания, образуют множество Ω = {12, 13, …, 19, 21, 23, …, 29, …, 91, 92, …, 99} - пространство элементарных исходов. Множество Ω содержит 72 числа. Так как появление всех этих чисел равновозможно, то для вычисления вероятности события можно применить формулу классической вероятности , где n – число всех исходов, а m – число благоприятных исходов события (исходов, при которых наступает событие А). Благоприятные исходы в нашем случае – это числа 12, 24, 36, 48. Таким образом, всего исходов n = 72, благоприятных исходов m = 4, и, следовательно, вероятность события A равна .

Пример 2. На плоскости начерчены две концентрические окружности, радиусы которых 5см и 10см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадает также и в кольцо образованное построенными окружностями.

Решение.

Вероятность попадания точки в кольцо определяется отношением площади кольца к площади большой окружности.

. .

Искомая вероятность .

2. Теоремы сложения и умножения вероятностей. Вероятность появления хотя бы одного события.

Надо знать: операции над событиями, виды событий, формулы вероятности суммы и произведения двух и более событий.

Разделы литературы: [1] гл.2, §1-3, гл. 3, §1-5; [2] гл.2, §1, 2.

Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

.

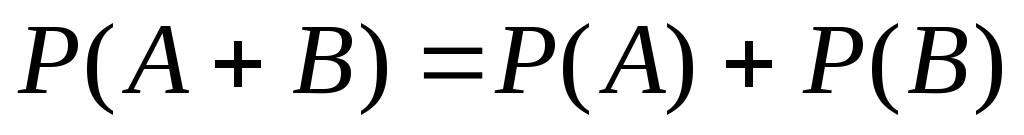(1)

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

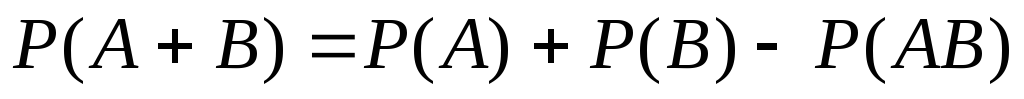(2)

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событии уже наступило:

.

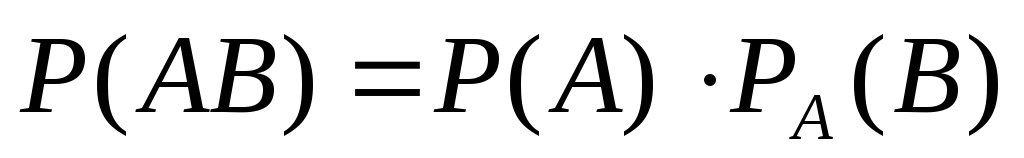(3)

Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

.

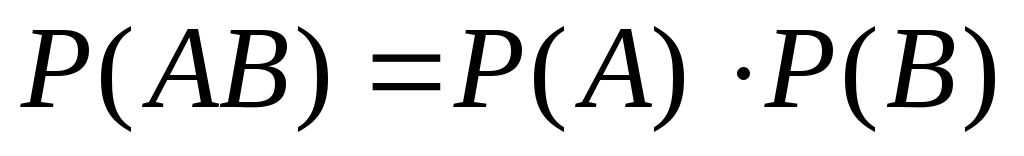(4)

Вероятность появления события А, состоящего в появлении хотя бы одного из событий A₁, A₂, …, A_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :

.

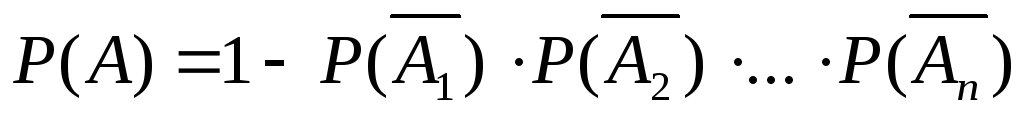(5)

Если все n событий имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий

,

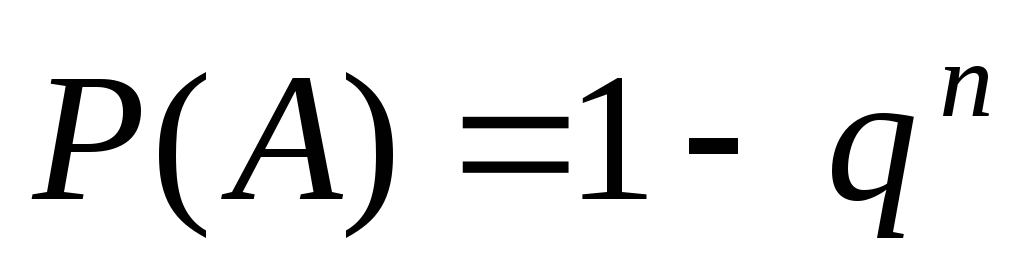(6)

где q = 1 – p.

Пример 3. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) три экзамена; б) только один экзамен; в) только 2-й экзамен; г) по крайней мере два экзамена; д) хотя бы один экзамен.

Решение.

Обозначим события:

А₁ – студент сдаст 1-й экзамен, ,

А₂ – студент сдаст 2-й экзамен,

А₃ – студент сдаст 3-й экзамен, .

Противоположные события - студент не сдаст 1-й, 2-й, 3-й экзаменысоответственно. ,,.

а) Событие В – студент сдаст все три экзамена состоит в совместном появлении событий А₁, А₂, А₃ (студент сдаст и 1-й, и 2-й, и 3-й экзамены), т.е. . Учитывая, что события А₁, А₂, А₃ независимы, по теореме умножения вероятностей получим

.

б) Событие С – студент сдаст только 2-й экзамен состоит в совместном появлении событий ,А₂, (студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены), т.е. . Учитывая, что события ,А₂, независимы, по теореме умножения вероятностей получим

.

в) Пусть событие D– студент сдаст один экзамен из трех. Очевидно, событие D произойдет, если студент сдаст только 1-й экзамен, или только 2-й, или только 3-й, т.е. . Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим

.

г) Пусть событие Е – студент сдаст, по крайней мере, два экзамена (иначе: «хотя бы два» экзамена или «не менее двух» экзаменов). Очевидно, что событие Е означает сдачу любых двух экзаменов из трех либо всех трех экзаменов, т.е.

.

д) Пусть событие F – студент сдаст хотя бы один экзамен. Вероятность этого события найдём по формуле (5) через вероятность противоположного события - студент не сдаст ни одного экзамена.

.

Ответ: а) 0,648; б) 0,018; в) 0,044; г) 0,954; д) 0,998.

Пример 4. В классе 11 девочек и 9 мальчиков. К доске вызвали двух учеников. Найти вероятность того, что они будут а) разного пола; б) одного пола.

Решение.

а) Событие Е, состоящее в том, что вызванные ученики разного пола, произойдёт в одном из двух случаев:

первой вызвали девочку (событие А), а вторым – мальчика (событие B)

или

первым вызвали мальчика (событие C), а второй – девочку (событие D),

т.е. E = A·B + C·D.

Так как девочек в классе 11, а всего учеников 11+9=20, то вероятность события А равна . Мальчиков в классе 9, а т.к. одного ученика уже вызвали, то учеников осталось 20–1=19, поэтому условная вероятность событияB равна . Аналогично получим вероятностии.

Окончательно получим

.

б) Событие A – вызванные ученики одного пола означает, что к доске вызвали либо двух девочек (обозначим как событие B), либо двух мальчиков (обозначим как событие C). т.е. A = B + С. События В и С являются несовместными, поэтому P(A) = P(B) + P(C). Вероятность вызвать первую девочку равна , а вторую(и девочек и учеников стало на одного меньше). Аналогично первого мальчика вызывают с вероятностью, а второго. Окончательно получим.

Ответ: а) 0,52; б) 0,48.