
Diskretka
.pdf
Diskretka.doc20.02.2014 |
71 |
|
|
|
|
|
Тело,укоторогомультипликативна |
ягруппаабелева,называется |
полем. |
|
|||
Отношения |
|
|
|
отношения, |
||
Фундаментпонятиемдискретнальтематикиявляетсяпымойнятие |
|
|
|
|||
которобозначенияиспдляльзуютсвязимеждуобъектамиилипонят. ями |
М назывдекартовопроизведениеетсядвух |
|
|
|
||
Квадратоммножества |
|
равныхмежду |
|
|||
собоймножеств: |
М× ММ= |
2.Бинарнымотношением |
Т вмножестве |
М называется |
||
подмножесегоквадра: таво |
T M 2 .Элементы |
тi,и тj, находятсявотношении |
T,если |
|||
(mi , mj ) T . |
|
|
|
|
|
|
Граф |
|
|
|
|
T M 2 |
|
Совокупность множества М сзаданнымвнембинарнымотношением |
|
|||||
называется графом G: |
|
|
|
|
|
|
|
|
G = M ,T , |
|
|
|
|
где М - носительграфа |
(множество вершин);Т |
- сигнатураграфа |
(множество дуг). |
|||
Рассмотримзадабиотношенияиеарнп мощьюго |
|
матрицысмежности |
и |
|||
фактор-множества. |
|
|
|
|
|
|
Матрицасмежности |
|
|
|
|
|
|
Приматрзадаичспндвумернуюииользуюттаблицу |
|
|
— матрицусмежности, |
М. |
||
каждстрстолбцу( )кйоторойевзаимнооднсопоставляютзначноэлементмножества |
|
|
|
|
||
Тогдакаждаяклетка |
(i, j) взаимнооднозначнос |
оответствуетэлементаммножества |
|
|
М2. |
|
Клетку (i, j),котсоотвраяэле,принадлежащемутствуетменту |
T M 2 ,как -тоотличают, |
напрзачерняютилимерпомв щаютдиницу;остальныеклеткиоставляют |
|
незачернеилизаписываютнихулиными |
. |
Пример. |
|
РассмотримпредложеннуюфонНейманомблок |
-схемуЭВМ,котоизстоитрая |
множестваустройств |
|
Фактор-множества иф актор-алгебра
|
Еслиотношение |
R обладасвойс:рефлексивтвамтраметричное, зитивное |
|
M,томножество |
|||||
т.е.являетсяотношениемэквивалентност |
|
иили(~≡илиЕ)намножестве |
|
||||||
классовэквиназываетсялентностифактмн множестважествомр |
|
|
|
M относительно |
|||||
эквивалентности R иобозначается M/R |
M R {[x]R }x M |
|
|
||||||
|
Здесь |
[x]≡ |
естьподмножествоэлементовмножества |
M |
эквивалентных x |
||||
|
|
|
|||||||
[x]≡ {y |
|
y M & y ≡ x},называемых |
классомэквивалентности |
. |
|
||||
|
|
||||||||
|
Изопределенияфактор |
-множестваследует,чтооноявляетсяподмножеством |
|
|
|||||
булеана: |
M R 2M . |
называется отождествлением |
|
||||||
|
Функция natR : M → M / R |
иопределяется |
|||||||
следующимоб |
разом: |
|
natR(x) [x]R |
|
|
||||
|
|
|
|
|
|
|
|
||
Теорема. |
Фактор-алгебра Fn/~изоморалгебребулевыхфункцийна |
Bn |
|
||||||
Доказательство. |
ξ: Fn/~→ |
Bn |
|
|
|
||||
Искомыйизоморфизм |
определяетсяпоследующемуправилу:классу |
|
|
||||||
эквивалентности ~(φ) |
сопоставляетсяфункция |
|
fφ, имеющаятаблицуис |
тиннпростиизвольной |
|||||
формулыизмножества |
|
~(φ).Посколькуразнымклассамэквивалентностисоответствуютразличные |
|
|
|||||
таблицыистинности,отображение |
ξ инъе,атаккакдтивнолюббулевойяфункции |
|
f из Вп |
||||||

Diskretka.doc20.02.2014 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
найдетсяформула |
|
|
|
|
|
ϕ Φn ,представ ляющаяфункцию |
|
|
|
|
|
|
|
f, отображение |
|
ξ сюръективно.Сохранение |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
операций , , |
|
|
|
, 0,приотображении1 |
|
|
|
ξ проверяетсянепосредственно.ЧТД. |
|
|
f Bn ,неявляющейсяконстантой |
|
|
|
|
0, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Потеофункциональнойремеполнотекаждойфункции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
соответствуетнекотораяСДНФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ,принадлежащаяклассу |
|
|
|
~(φ) = ξ-1(f) формул,представляющих |
|
|
|||||||||||||||||||||||||||||||||||||||||
функцию f.Возадникаетхождениячавклассе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~(φ) |
|
дизъюнктивнормальформы, ной |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
имеющейнаибпрстроениелеестое. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Целыечислапомодулю |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Данокольцоцелыхчисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<Z; +, ! >. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Напомним.А |
лгебра <М, |
|
|
, +>,котпумножениюраяявляетсямультипликативным |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
гру,псложениюпидом |
|
|
|
|
|
|
|
|
|
|
|
|
|
— абелевойгруппой,причемумножениеспраслеваязано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
сосложениемзакона и |
|
|
|
|
|
|
|
|
дистрибутивности называется кольцом. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Возьмемцелоечисло |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m>1.Зададимотношениеэквивалентности |
|
|
|
|
|
|
|
≡m намножестве |
|
|
||||||||||||||||||||||||||||||||
целыхчисел |
Z последующемуправилу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
b ≡m a |
b - a = m q длянекоторого |
q Z . |
|
|
|
|
|
|
|
|
A.К лассомэквивалентности |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Напомним.Пусть |
|
|
|
|
|
|
|
|
Е – |
эквивнмножествеалентность |
|
|
xEy}. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
элемента x A называется множество E(x) →{y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Классэквивалентностиэлемента |
|
|
|
|
|
|
|
|
|
|
|
|
|
a помодулю |
|
|
m – этомножество |
{a + m q |
|
q Z} = {…, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
-3m+a, -2m+a, -m+a, a, m+a, 2m+a, 3m+a, …},котороеобозначаетсячерез |
|
|
a+Zm илипросто |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Пример.Если |
|
|
m=5, |
топрисоответственно |
|
a=0, |
1, |
2, 3, |
4 классыэквивалентности |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
элементов a помодб5усоодутлюравныветственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= {...−15,−10,−5,0,5,10,15,...}; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= {...−13,−8,−3,2,7,12,17...} |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
1 = {...−14,−9,−4,1,6,11,16...}; |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= {...−12,−7,−2,3,8,13,18,...}; |
|
|
= {...−11,−6,−1,4,9,14,19,...}. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Такимобразом,множество |
|
|
|
|
|
|
|
|
|
Z разбиваетсянанепересекающиесяподмножества |
|
|
|
|
|
|
|
|
, 1, |
|
, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
, |
|
,т.е. Z = |
|
1 |
|
|
|
|
|
|
|
|
ипопарные |
|
|
|
ресечения |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
4 |
2 |
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
0 |
3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
∩1 = ит.д. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Напомним.Множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
x A} |
называется |
фактор-множеством |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A/ E →{E(x) |
|||||||||||||||||||||||||||||||||||||||||||||||||
множество A поотношению |
|
E. |
|
|
|
Z поотношениюцелыечислапомодуявляется5 ю |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Фактор-множествомцелыхчисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
множество Z / ≡5 = {0,1, 2,3, 4}.Мощн осэтмногоьравнажества5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Вобщемслучаемножество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z / ≡m = {0,1, 2,3,...m −1} содержит m элементов. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Вместозаписи |
|
|
b ≡m a пишут b ≡ a (mod m) читается« |
b равно a помодулю |
|
m»или« |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||
сравнимо с a помодулю |
m». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zm иназывается |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Множество |
Z / ≡m |
|
обозначаетсятакжечер |
|
|
|
|
|
|
|
|
|
множесвычетвомов |
|
|
|||||||||||||||||||||||||||||||||||||||||||
или множецелыхчипосмодулютвомел |
|
|
|
|
|
|
|
|
|
|
|
|
|
m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Конгруэнции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = <A; Σ> (Σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
Конгруэнцией наалгебре |
|
|
|
– сигнатуалгебсостоиттолькоризаы |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
функциональсимволназыва) такоотнэквивалентныхошениется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ости |
θ A2 ,при |
|||||||||||||||||||||||||||||||||
которомдлюбогоя |
|
|
|
|
|
|
|
n N ,любого |
n-месимволатного |
|
|
|
|
f |
Σ произвнабольныхров |
|
|
|
(a1, a2, |
|||||||||||||||||||||||||||||||||||||||||||||
… ,an), (b1, b2, … ,bn) An,если a1θb1, a2θb2, …, anθbn, то f(a1, a2, … ,an)θ f(b1, b2, … ,bn),т.е. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
всеоперациисогласованыотношениемэквивалентности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
Пример.Длядвухместноперациисложенияэтовыглядиттакй: юбых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x и y из A и |
||||||||||||||||||||||||||||
любых a θ(x), |
b θ(x) элемент a+b принадлежитклассу |
|
|
θ( x+y). |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||

Diskretka.doc20.02.2014 |
|
|
73 |
|
|
||
Лемма. Отношение ≡m являетсяконгруэнциейнаалгебре |
<Z; +, ! >. |
|
|||||
Наиобщийделительольший |
|
чисел a и b обозначается (a, b)или НОД( |
a, b). Двацелых |
||||
числа a и b называются взаимнопростыми |
если (a, b) = 1. |
a-1 |
|||||
Теорема. Тогдаитолькотогдаэлемент |
|
a кольца Zm имеетобратный(..элемент |
|||||
такой,что |
a a-1 = 1),когда( |
a,m) = 1. |
|
|
|
||
Теорема. Кольцовычетов |
|
<Zm; +, ! > тогдаитолькотогдаявляетсяполем,когда |
m |
||||
простоечисло |
. |
|
|
|
|
|
|
Замечание |
|
|
|
|
|
|
|
1Для.пост |
|
роениялогическойтеориииспользуютсяформализованныеязыкинепустое( |
|
|
|||
множестваалфавита,синтсемантикиксиса),которыеявляютсясредствомпознанияра |
|
|
|
|
|
||
средствомвыражениямысли. |
|
|
|
|
|
|
|
δ = ‹ A, S1, S2› (A- символыалфавита, |
S1- синтаксис, |
S2- семантика). |
|
||||
2Врамках. формализированныхязыкстр ятсягическиетеории,помощью |
|
|
|
||||
которыхрешаютсялогическиезадачи. |
|
|
|
|
|
|
|
3Во.множествеформулязыкавыделяютклассформул |
|
x не x = 1 |
|
- аксиомылогич( .закон,базис) |
|
||
Например,выражение |
|
|
|
|
|||
4Выделяю. |
тмножепер,т.е.спомхтвопереходоввощьюотоднойформулык |
|
|
|
|||
другойнаходятправильныеумозаключения.
Контрольныевопросы
Лекция№ 7
Дляматематиков |
XIX в.занимавшихся, алгебройлогики, |
|
наиболееважнойпроблемойбылоразвитие |
|
технических |
приемовоперированиясэлементарнымиутвержден ями |
|
|
булевалгебры,подобныхйтем,которыеимеютсяв |
|
|
элементаалгеб. реной |
|
|
Х.Карри.Основанияматематлогик.М.Мир:, ческой |
- |
|
|
|
1969,стр. 420 |
Diskretka.doc20.02.2014 |
|
74 |
|
|
|
|
ЭЛЕМЕНТЫТЕОРИИГРАФОВ |
|
|
||
Графы - математическиеобъект |
|
ы. |
|
|
|
Теорияграфовприменяетсятакихобл, физикастхимияк, ,теориясвязи, |
|
|
|
|
|
проектированэлектротехникаЭВМ, ,маш,архинос, сследованиеектураро |
|
|
|
|
|
операц,генетика,пс ,социологияйхология,экономика,антропология. |
|
|
|
|
|
Этатеориятесносвязанатакж |
|
есомногимиразделасредиматема, которыхики |
|
||
теориягрупп,теорияматриц,численныйанализ,теориявероятностей,топология |
|
|
|
|
|
комбинаторныйанализ. |
|
|
|
|
|
Единогообщепрграфаедин.Взависимостиеятоголенияотрешаемойзадачи |
|
|
|
|
|
принтоилиномаопрется |
еделение,котпо,рыехэтонодножитоже. |
|
|
||
ТеографовияодиласьнаберН,евСгвыахнкт |
|
|
-Петербурге,иосновоположником |
||
являетсяЛеонардЭйлер,публиковавш1736решениезадачКенигсбергскихмостахй. |
|
|
|
|
|
1736год. |
Эйлердоказывает,чтозадача |
|
Кёнигсбергскихмостахнеим .шенияет |
|
|
ЦентрчастьКальинаяинграда |
– |
этодваберегарекиПерголядваостэтой.екива |
|
|
|
Островасоединенымеждусобмостодногойстрм2+2мосберегамивастау |
|
|
|
|
|
другого1+1Всегом7..Задастов:обойтичсеа |
|
|
етыречастисуши |
– дваберегаидва |
|
ост,пропокаждодномувайдямоступ разу. |
|
|
|
|
|
СледующиешагивразвиттеорграфовпринадлежатииГ.Кирхгофу,применившему |
|
|
|||
теографовию1847.ктеорииэлектрическихцепейА.Келли,разработавшему1857г. |
|
|
|
|
|
теориюдеревьипримектеорвнхимвшеизомеровческих. у |
|
|
|
|
|
1930год. |
КазимирКуратовскийдоказывает,чтозадачатрехдомахколодцахне |
|
|
||
имре.шенИмеетсятридоматрияколодца.Нужнопролтрокаждоготьтпидомака |
|
|
|
|
|
ккаждомуколодцутак,чтобы |
онпересекалисье. |
|
|
||
Родивпреишголоволомокисьениизаниматзадач, XXтеориякельныхграфов |
|
|
|
|
|
сталамощнымсредствпроблемрешениянауког,шиприложимостьхрокаястала |
|
|
|
|
|
дополнитестимуломеебуразвитияного.ьнымСамтерминграф""ровнона20 |
|
|
|
0летмоложе |
|
этойе, введенрииупотребление1936г.выдающимсявенгерскимматематикомД. |
|
|
|
|
|
Кенигом. |
|
|
|
|
|
1976год. |
АппиХеспомйкенлькомпьютеращью,перебравоколо2000контр |
|
- |
||
вариантовпоказали,чтод статочно4 |
|
-ёхкрасокдлярасккарты.К скирта |
|
– эторазбивка |
|
поверхннепересекающимисяостибластями. |
|
|
|
|
|
Определение. |
|
Неориентированнымграфом |
Gназывается |
||
|
|
|
|||
|
|
|
множествоN вместе=множеством{x,y,A..}= |
|
|
|
|
|
{(x,y),некоторыхнеупорядоченных..}(пар),где |
|
|
|
|
|
множествоконечноN ..чис( егэлементов |
|
|
|
|
|
конечно),авомножествеAнетэлементоввидах,(х). |
|
|
|
|
|
ЭлемемножестваNазываюттывершилинами |
|
|
|
|
|
узла,элемеиножестваAтыазываютребрами. |
|
|
|
|
|
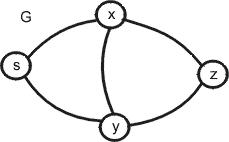
Обозначениенеориентированногографа: G=(N,A) |
|
|
неориентированногографаG. |
|
N = |
{x,y,s,z} |
- множествовершин |
|
|
|
|
|
||
A = {(sx),(sy),(xz),(xy),(yz)} - множреберориентированногоствографаG |
|
||||
Граф,ве, шинаебро |
|
|
|
|
|
Под неориентированнымграфом |
|
(иликороче |
графом) |
будемпониматьтакую |
|
произвольнуюпару |
G = <V, E>,что |
|
|
|
|
E {{u, v}: u, v V u ≠ v}.
Ориентированныморграфом( ) |
будем называтьтакуюпроизвольнуюпару |
G = |
<V, E>, что E V V . Вобоихслучаяхмножества |
V и Е будемназыватьсоответственно |
|
Diskretka.doc20.02.2014 |
|
|
75 |
|
|
|
|
множеством вершин имножеством |
ребер |
графа G. |
Элементымножества |
Е дляорграфа |
|||
называются дугами |
|
|
|
|
|
|
|
Граф G задаетсямно |
жествомточекили |
|
вершин х1, х2, . . ., хn |
,котороеобозначается |
|||
через X, имножествомлинилий |
ребер a1, a2, . . ., an , котороеобозначаетсясимволом |
A, |
|||||
соединяющихмеждусобойвсеиличастьэ очек.Такимобразом, |
(X,А). |
|
|
|
граф G |
полностью |
|
задаетсяи(обозн |
ачается)парой |
|
|
|
|
|
|
Графобычизображаетсянплоскостиввидемножесточек,соотваетствующих |
|
|
|
|
|||
вершинам,соединяющихлиний,соотвр .Дугатствующихбраморграфе |
|
|
|
|
|
|
|
изображалиниейсостр,указывающейлкойтсяориентдуги,.. правлениециюот |
|
|
|
|
ее |
||
началакконцу |
|
{и, |
v}, |
или <и, v> |
(угловыескобкиисподльзуются |
|
|
Л,иниязображающаяребро |
|
||||||
|
|
обозначениядугорграфа. |
),соединяетточки, |
|
|||
|
|
изображающиевершины |
и, v причемвовторомслучае |
|
|||
|
|
стрелкаобозначаетнаправлениеот |
|
и к v (рис. 1.1). |
|||
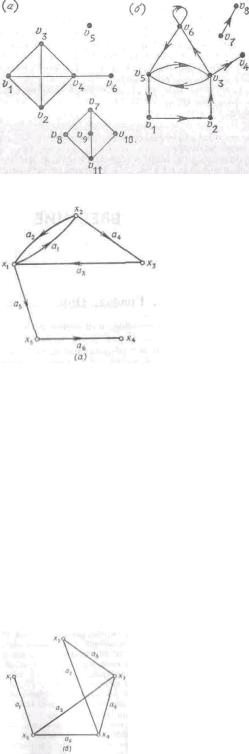
|
|
|
Рис. а) 1.1. |
Неориентированныйграф; |
б) |
||
Ориентированныйграф.
Дуга,ориентированныйграф
Еслиребраизмножества |
А ориентированы,чтообычно |
||
показываетсястрелкой,тоназываютсяи |
дугами, |
играфстакими |
|
ребраминазывается |
|
ориентированным графом |
|
Пример.рис( |
.а))( . |
|
|
|
|
Соответствие |
|
|
G состоитвзадании |
|||||
Другое,употребляемоечащеописаниеориентированногографа |
|
|
|
|
|
|
||||
множествавершин |
|
Х и соответствия Г,котпоказываетрое,какмеждусобойсвязаны |
|
|
||||||
вершины. |
Соответствие Г называется отображением множества Х в X, аграф |
вэтом |
||||||||
случаеобозначаетсяпарой |
G =Г)(X,. |
|
|
|
|
|
|
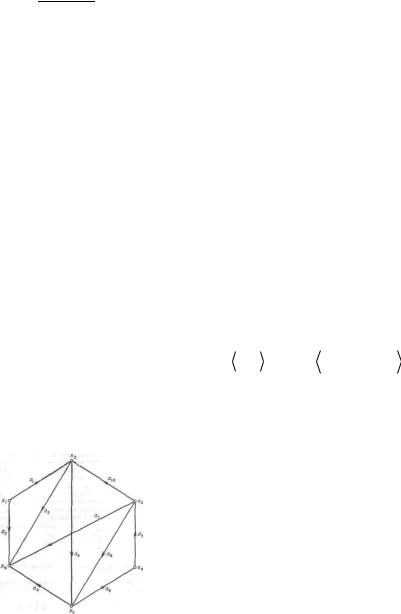
х2 и х5 являютсяконечными |
||
Дляграфанарис.)имеем( |
|
Γ(x1 ) ={x2 , x5},т.е.вершины |
||||||||
вершид,укоторыхгнамичальнойвершинойявляется |
|
|
|
|
|
|
х1 |
|
|
|
Γ(x2 ) ={x1, x3}, |
|
|
|
|
|
|
|
|
||
Γ(x3 ) = {x1}, |
|
|
|
|
|
|
|
|
|
|
Γ(x4 ) = — пустмн,ожество |
|
|
|
|
|
|
|
|
||
Γ(x5 ) = {x4}. |
|
|
|
|
|
|
|
|
|
|
Неориентированныйграф |
|
|
|
|
|
|
|
|
||
|
|
Еслиребранемеюторие,тографназываетсятации |
|
|
|
|
||||
|
неориентированным |
(неориентдублликатрованный |
|
|||||||
|
неориентированныйдвойник |
|
)В.случаекогда |
G = (X,А) |
является |
|||||
|
ориентироваграфомнеучитываетсянаправленностьнымдугиз |
|
|
|||||||
|
множества А, тонеориентированныйграф,соответствующий |
|
G, |
|||||||
|
обозначаетсякак |
|
|
|
|
|
|
|
||
|
G |
= (X , A). |
|
|
||||||

Diskretka.doc20.02.2014 |
|
|
76 |
|
|
|
Пример.рис(.б) |
|
|
|
|
|
|
Ориентированнымграфом |
|
или орграфом называетсямножествоN вмест= {x,y,..} |
ес |
|||
множествA некоторых= {(x,y),упорямпаргдемножество..очен}( коN ..(ыхечно |
|
|
|
|
|
|
чисегоэлементовконечно),авомножественетAэлементоввидах,х)(Элементы. |
|
|
|
|
|
|
множестваNназывают |
вершинами или узлами,элемемножестваAазываютты |
дугами или |
||||
ребрами.Обозначениенеориентированногографа: G=(N,A) |
|
|
|
|
||
Вотличиеорграфау пары(x,y)упорядочены. |
|
|
|
|
|
|
N = {x,y,z,s} - вершины |
|
|
|
|
|
|
A = {(sx),(sy),(xz),(xy),(yz)} |
|
|
|
|
||
дуга(sx): s |
- началодуги; x |
|
- конецдуги |
|
|
|
дуга(yz): y |
- началодуги; z |
|
- конецдуги |
|
|
|
Издвух |
определениймыувидели,чтографыбываютдвухтипов |
|
|
- неориентированные |
||
иориентиро.Внашемкурсемыбудемвосновноманныезаниматьсяориентированными |
|
|
|
|||
графами. |
|
|
|
|
|
|
Дляудобствавместормор" инаентированныйграф"будемупотреблятьтермин |
|
|
|
|
||
гр(таупрощефкое |
ниедопусвомногихкнигахается). |
|
|
|
|
|
Отметим,чтоизопределениявытек,чтогрнеаможетфебытьпет,..реберель, |
|
|
|
|
|
|
соединяющихвершинысамисобой. |
|
|
|
|
|
|
Инцид,смешграфнтностьнный |
|
|
|
|
|
|
Еслиребро |
е имеетвид |
{и, |
v } или <и, v>, тобудемговорить,чторебро |
е инцидентно |
||
вершинам и и v,втовремякаквершины |
|
|
и и v смежны междусобой. |
|
||
Направлениепредполагаетсязаданнымотпервойвершиныковторой,когдадуга |
|
|
начальной и конечной вершин,т..двумя |
|||
обозначаетупорядпар,соосченнойизтоящей |
|
|
||||
концевыми вершинамидуг.Так,нап,нари.а)обозначение(смер |
|
(х 1, х2), относитсякдуге |
||||
a1 ,а (х 2 ,х 1) — к дуге a2.Концевыевершиныдуги |
инцидентны своейдугеинаоборот,дуга |
|
||||
инцидентна своимконцевымвершинам. |
|
|
Смешанныйграф |
- вершинысоединеныдугами |
|
|
(a1, a2, a3, a4, a6, a7) иребрами (a5). |
|
|
|
|||
Эквивалентныйориентированныйграф |
Вслучаенеориентграфаил,исодержащегорованногофа |
|
|
|||
|
|
|
|
|||
|
идуги,неорие,предпнтированныебра,чт лагается |
|
|
|||
|
соответствие |
Г задаеттакой |
эквивалориентированный |
|||
|
граф,котпорый |
лучается изисходногогрзаменойфак ждого |
|
|||
|
неориентированнребрадвумяпротивопоголожно |
|
|
|||
|
направлдугами,соенныдиняющимитежесавершиныые. |
|
|
|||
При1с..графым, (,изобернар.исбаженные)(в()) |
|
Пример2. |
|
Так,например,дляграфа,приведенногона |
с.б),(имеем |
Γ(x5 ) = {x1, x3 , x4},
Γ(x1 ) = {x5} ит.д.
Обратноесоответствие |
|
x j X , длякоторыхв |
||||
Поскольку Γ(xi ) представляетсобоймножтакихршинство |
||||||
графе G существуетдуга |
(х i, хj), точерез |
Γ−1 (x ) естественнообозм ожествовершиначить |
|
|||
|
|
|
|
|
i |
|
хk,длякоторыхв |
G существуетдуга |
(х k, хi). Отношение Γ−1 (x ) принятоназывать |
обратным |
|||
|
|
|
|
|
i |
|
соответствием. |
|
Дляграфа,изобнараис),(имеемженного |
|
|
|
|
Γ−1 (x ) ={x , x |
} |
|
|
|
||
1 |
2 |
3 |
|
|
|
|
Diskretka.doc20.02.2014 |
77 |
|
Γ−1 (x |
) |
={x } ит.д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Длянеориентированногографа |
Γ−1 (x ) = |
(x ) длявсех |
|
|
x X . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
i |
|
|
|
|
|
|
|
Когдатображение |
Г дейстненаоднувершинуует,анамножествовершин |
|
|
|
|
|
|
|
|
|
|
||||||||
Xq |
={x1, x2 ,..., xq },топод |
Γ(Xq )) понимаютобъединение |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Γ(x1 ) |
|
Γ(x2 ) ... |
Γ(xq )- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
т.е. |
Γ |
(Xq ) |
|
являемножтакихсявествомршин |
|
|
|
x |
j |
X ,чтодлякаждойизних |
|
|
|
|
|||||
|
|
U |
U U |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
существуетдуга |
|
|
(х i, хj) в G,где |
xi X q . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример. |
|
|
|
|
|
|
Γ({x , x }) |
= {x , x , x } и Γ |
({x , x |
}) = {x , x , x |
}. |
||||||||
|
Дляграфа,приведенногона |
|
ис.а),( |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
5 |
1 |
3 |
|
4 |
1 |
3 |
2 |
5 |
1 |
|
|
Отображение Г(Г(х |
i)) записываетсякак |
Г2(х i).Аналогичнотр«» йноетображение |
|
|
|
|
|
||||||||||||
Г(Г(Г(х |
i))) записываетсякак |
Г3(х i) ит.д. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дляграфа,показанногонарис.),(имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Г2(х 1)Г(Г=( |
|
x1)) =Г({х |
2,х 5}) = {x1, x3, x4} |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Г3(х 1)Г(Г= |
|
2(x1))Г({= |
x1, x3, x4}) = {x1, x2, x5} ит.д. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Аналогичнопонимаютсяобозначения |
|
|
Г-2 (xi),Г -3(xi) ит.д |
|
|
|
|
|
|
|
|
||||||||
Изоморфизмграфов |
|
G1 = <V1, E1> и G2 = <V2, E2> изоморфны( |
G1 ~ G2) еслиуществуетбиекция |
|
|
|
||||||||||||||
|
Дваграфа |
|
|
|
|
|||||||||||||||
φ: V1 → V2 сохраняющиесмежность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
е1 = (u,v) E1 |
е2 = (φ (u), φ (v)) E2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Теорема. |
Изоморфизмграфовестьношениеэквивалнтности |
|
|
|
|
|
. |
|
|
|
|
|
|||||||
|
Графы G = <V, E>, G' = <V', E'> изоморфны, |
еслиуществ |
|
|
уеттакоднозначноевзаимно |
|
|
|
||||||||||||
отображение |
|
f |
|
из |
V |
на |
V',чтодляпроизвольных |
|
|
|
|
|
u, v V |
|
имеем |
|||||
{u, v} E { f (u), |
f (v)} Eʹ |
( u, v E f (u), |
f (v) |
Eʹвслучаеориентированных |
|
|
|
|||||||||||||
графов)Обычно. изомграфынеразличаютсярфныемеждусобой.
Путь,орие |
нтированныймаршрут |
|
|
|
Путем (или ориентированныммаршрутом) |
ориентирографаназываетсяанного |
|||
|
последовательдуг,кот нройршинавсякойчдугиаяость, |
|
|
|
|
отличнойпоследней,являетсяначальнойвершинойследующей. |
|
|
|
|
Пример. |
Нарис.последовательности2 |
дуг |
|
|
а6, a5, a9, a8, a4 |
(1.1) |
|
|
|
a1, a6, a5, a9 |
(1.2) |
|
|
|
a1, a6, a5, a9, a10, a6, a4 |
(1.3) |
|
|
|
являютсяпутями. |
|
|
|
|
|
Путем вграфе G = <V, E> назповемследовательностьвершин |
|
||
|
V0, |
V1,..., Vk такуючто |
k ≥0 п vi - vi+1 (или vi → vi+1,еслиграф |
G — |
|
ориентированный), |
i = 0, ..., k - 1.Терминпуть«»втеорииграфовиспользуетсятольков |
|
|
||
отношенииорграфов,дляиспользуютсятерминыцепь«»илимарш« »Ве. ршиныут |
|
k —длиной пути. |
|||
V0 и Vk будемназыватьс |
|
оответственно началом и концом пути,ачисло |
|||
Путь,началоиконецкотс роговпадают,будемназывать |
|
циклом.Введтакерминнный |
|
||
«цикл»втеорииграфовиспользуетсятольковотнграфов,шениидляорграфов используетсятерминконтур« ».

Diskretka.doc20.02.2014 |
|
|
|
|
78 |
|
|
|
|
|
Если всершиныпути |
|
|
V0, V1,..., Vk различны,тобудемговорить |
|
обэлементарном |
|||||
пути.Соответственноцикл |
|
V1,..., Vk (V1 = Vk) будемназывать |
|
элементарным, |
есливершины |
|||||
V1,..., Vk различны. |
|
|
|
|
|
|
|
|
|
|
Маршрут естьнеориентдвойн« »пут,иэтрпиокрвнятиеассматнный |
|
|
|
|
|
ривается |
||||
техслучаях,когдаможнаправленностьюпренебречьдугвграфе.Такимобразом, |
|
|
a1, a2 ,..., aq ,вкоторойкаждоеребро |
|
|
|||||
маршрут |
естьпоследовательностьребер |
|
|
ai ,за |
||||||
исключ,возможно,пениемрвогопоследнегоребер |
|
|
|
|
,связаноребрами |
ai−1 и ai+1 своими |
||||
двумяконцевымивершинами. |
|
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
Последовательностидуг |
a2 , a4 , a8 , a10 |
|
(1.4) |
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
a2 , a7 , a8 , a4 , a3 |
|
(1.5) |
|
|
||
вграфе,изобнар.исаженномявляютсямарш2, ;ченадрсимволомутамидугозначает, |
a2 , a7 , a8 , a4 , a3 |
|
(1.6) |
|
|
|||||
|
|
|
|
|
|
|
||||
чтоееориентациейпренебрегают,..дугарассмакакнеориривае.нбротированноеся |
|
|
|
|
|
|
||||
Смежныедуги,смежныевершины,степень |
|
|
|
|
шины |
|
|
|
|
|
Дуги а=х ( i,х j), |
хi ≠х j, |
имеющиеобщиеконцевыершины,называются |
|
|
|
смежными. |
||||
Две вершины хi и хj называются смежными, |
есликакая |
-нибудьиздв хг |
|
(х i,х j) и (х j,х i) |
||||||
илиобеодновременноприсутствуютграфе. |
|
|
|
|
|
|
|
|
вершины |
|
Есливершиныxнеориентированноy |
|
|
гографаGсоединеныребр(x,y),т м |
|
|
|||||
называются смежными,впротивномслучае |
|
- несмежные. |
|
|
|
|||||
ДлянеориентироваграфаG:вершины,смежвершинеs ногоые |
|
|
|
|
|
- этоиxсмежныеy; |
||||
вершинеx |
- этоs,y,z;смежныевершинеz |
|
|
- этоx,y;смежныевершинеy |
|
|
- этоs |
,x,z. |
||
Ствершиныпень |
|
опредекакчисребер,инцидентныхлимоей.Вершинунулевой |
|
v5 нарис. а1)Длявершин..1, |
|
|||||
степенибудемназывать |
|
изолированной (например,вершина |
|
исхода (число |
||||||
орграфаопределяются |
полустепенизахода |
(числозахввершдящдуг)и инух |
|
|
||||||
выходящихдуг)Степень. вершиныопределяетсякаксуммаполустепенейзаходаиисхода |
|
|
|
|
|
|
|
|||
Компонентнаясвязность |
|
|
|
|
|
|
|
|
|
|
Пусть G = <V, E> |
—произвольнеориеграф,ипустьнтированный |
|
|
|
v V . Пусть А |
|||||
— множествотехвершин |
|
u V , к которымсуществуетпутьиз |
|
v. Множество А вместе |
||||||
ребграфами |
G, инцидентнывершинаиз ми |
|
А,определяетнекоторыйподграф, |
|
||||||
называемый компонентойсвязности |
|
графа G. Очевидно,чтомножествавершинкомпонент |
|
|
||||||
связностипроизвольногографапонепересарно |
|
|
|
|
екаются. |
|
|
|
||
Ориентированнаяцепь |
|
|
|
|
|
|
|
|
|
|
Еслиграфимеетциклнеобязательно( простой),содевсерёбраграфажащийпо |
|
эйлеровымциклом |
|
|
|
эйлеровым |
||||
одномуразу,тотакойциклназывается |
|
|
|
|
,аграфназывается |
|||||
графом. |
|
|
|
|
|
|
|
|
|
|
Ориентированнойцепью |
|
(проспу)илит,(корочеь й |
|
|
орцепью) |
называетсятакойпуть, |
||||
вкоторомкаждиспользуетсядуганебольшеодногораза |
|
|
|
|
|
|
. |
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
Пути( |
а6, a5, a9, a8, a4)и( |
a1, a6, a5, a9)являютсяорцеп,апуть( ми |
|
|
a1, a6, a5, a9, a10, a6, a4) |
|||||
неявляеттаким,посдугаколькуя |
|
|
a6 внемиспользуетсядв |
|
ажды. |
|
|
|||
Простаяорцепь |
|
|
|
|
|
|
|
|
|
|
IIростойорцепью |
|
(элементарныйпуть)называетсятакойпуть,которомкаждая |
|
|
|
|
||||
вершинаиспользуетсянебодноголеераза. |
|
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|

Diskretka.doc20.02.2014 |
|
|
|
|
79 |
|
|
|
|
|
Путь( a1, a6, a5, a9)являетсяпрорцепьюстой,апути( |
|
|
|
а6, a5, a9, a8, a4 1и.1)(1.3) |
— нет. |
|||||
Простая орцепьявляетсятакже |
|
орцепью,нообратутверждениееверноое. |
|
|
|
|
||||
Пример1Путь.(1является.1)орцепью,нонепрорцепьюстой. |
|
|
|
|
|
|
|
|
|
|
Пример2Путь.( |
a1, a6, a5, a9)являетсяорцепьюипрорцепьюстой. |
|
|
|
|
|
||||
Пример3Путь.(1неявляется.3)ниорцепью,нипрорцепьстой |
|
|
|
|
|
|
ю. |
|
|
|
Цепи,простыецепи |
|
|
|
|
|
|
|
|
|
цепи |
Точнотакже, былиакопределеныорцепиорцестые,мопжноределить |
|
|
|
|
|
|
|
|||
(простоймаршрут)и |
простыецепи |
(элементаарш). |
рныйут |
|
|
|
|
|
||
Пример. |
|
|
|
|
|
|
|
|
|
|
Маршрут(1естьцепь.4)ипростаяцепь,маршрут(1.5) |
|
|
|
|
— цепь,нонепростаяцепь, |
|
||||
маршрут(1неявля.6)нице,ниптсяьюростойцепью. |
|
|
|
|
|
|
|
|
|
|
Путьилимаршрутможноизображатьтакжепоследовательностьювершин. |
|
|
|
|
|
|
|
|||
Пример. |
|
|
|
|
|
|
х2, х5, х4, х3, х5, х6 итакое |
|||
Путь(1можно.представить1) последовательностьювершин |
лезнымвтехслучаях,косуществляетсягдапоиск |
|||||||||
представлениечастооказываетсяболеепо |
|
|
|
|
|
|
||||
прорцепейстыхилипростыхцепей. |
|
|
|
|
|
|
|
|
|
|
Вес,стоимость |
G сопоставляютсяприп( )числасываются |
|
|
— дуге (х i, хj) ставится |
||||||
Инодуграфадам |
|
|
||||||||
всоответствиенекотороечисло |
|
cij называемое весом, |
или длиной, |
или стоимостьюценой() |
||||||
дуги. |
|
|
|
|
|
|
|
|
|
|
Связность |
|
|
связным,еслиуществуетсоединяющаяихпростая |
|
|
|
|
|||
Двевершиныграфеназ ваются |
|
|
|
|
|
|||||
цепь.Грнафзывается |
связным,есливсееговершисвяз. ны |
|
|
|
|
|
|
|||
Теорема. Графсвязентогдаитолькотогда, егонельзядапредставитьвиде |
|
|
|
|
|
|
|
|||
объедвухиненияграфов. |
|
|
|
|
|
|
|
|
|
|
Пусть G(V,E) – связныйграф, |
u и v – двеегонесмежныевершины.Двецепи< |
|
|
|
u, v > |
|||||
называются вершинно-непересекающимися, |
еслиунихнетобщихвершотличных, |
|
|
|
u и v. |
|||||
ТеорМенгера( ) ма |
. Пусть u и v – несмежныевершиныграф |
|
|
G. Наименьшеечисло |
||||||
вершинмножестве,разделяющем |
|
|
u и v равнонаибольчислувершемуинно |
|
|
- |
||||
непересекающихсяпростых |
<u,v>-цепей: |
|
|
|
|
|
|
|
||
|
|
max|P(u,v) | = min|S(u,v)| |
|
|
|
|
||||
Графсовзвешеннымидугами |
|
|
|
|
|
|
|
|
|
|
Граф G = (N, A) называется |
взвешенным,еслинамножестведуг |
|
|
A |
определена |
|||||
некотораяфункция |
l:→A R,которуюназывают |
|
весовойфункцией |
. |
|
|
|
|||
Темсамымввзвешенномграфе |
|
G каждойдуги |
x A поставленосоответствие |
|||||||
некотороедействительноечисло |
|
l(x).Значение l(x) называются длинойдуги |
x. |
|
||||||
Длялюбогопути |
Pi взвешенногографа |
|
G обозначающимчерез |
|
l(Pi) |
суммудлин |
||||
входящих Pi дуг,приэтомкаждчитываетсяугастолькораз,ск входитналькопуть. |
|
|
|
|
|
|
|
|
||
Величину l(Pi) называют длинойпути |
|
Pi ввзвешенномграфе |
G. |
|
|
|
|
|||
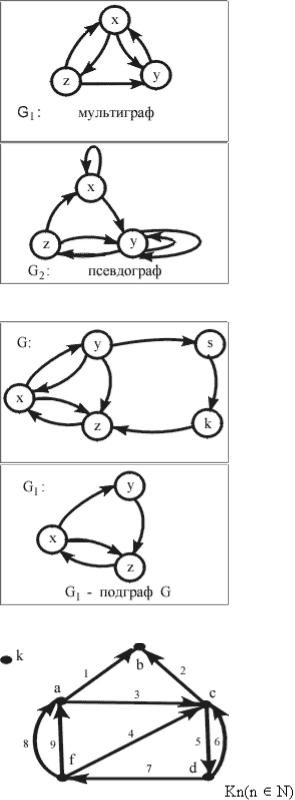
В мультиграфе недопускпетли,ноаверыются |
|
|
|
ршинмогутсоединятьсяболеечем |
|
|
||||
однимребром:этиребраназываюткратнымипротивоположными.
Diskretka.doc20.02.2014 |
80 |
Еслидопускаютсяпетли,протикратныевоположныеребра,получаем |
псевдограф. |
Определение. ПодгрграфанG фомзыграф,всеаетсяршиныребракоторого содержатсясредиве шинеберграфаG.
Дуги8,9 |
- |
называютсяпараллельнымикратными()Дуги. 5,6 |
- называются |
противоположными.Вершинаk |
- называетсяизолированной. |
|
|
Определение. |
Полнымграфом |
назыграфсвnаетсяершинамибезпетель, |
кратныхипротивоположныхдугориентация( |
безраз),укотороголюбыеичнадвершины |
|
соединеныдугой. |
|
|
