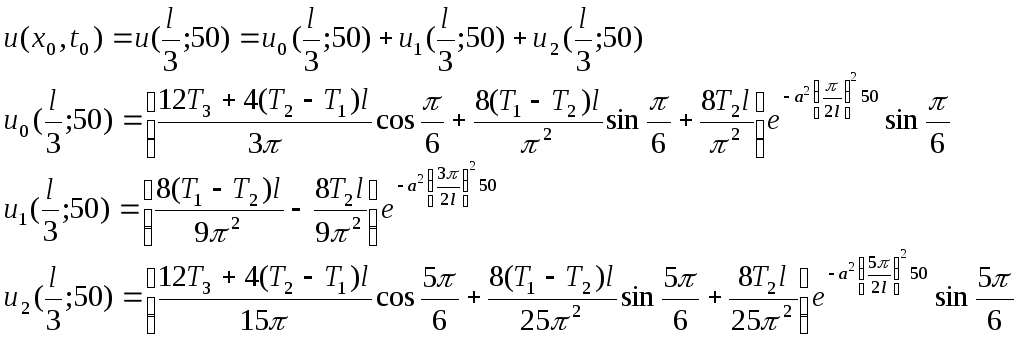Variant_12
.docВариант 12
1)Разложить в ряд
Фурье функцию
![]() ,
заданную с помощью графика. Построить
график суммы полученного ряда Фурье и
записать 4 первых ненулевых члена этого
ряда.
,
заданную с помощью графика. Построить
график суммы полученного ряда Фурье и
записать 4 первых ненулевых члена этого
ряда.
Функцию на графике
можно представить в виде:![]()
Разложим функцию
![]() в
ряд Фурье с периодом
в
ряд Фурье с периодом![]() :
:
![]() ,
где:
,
где:
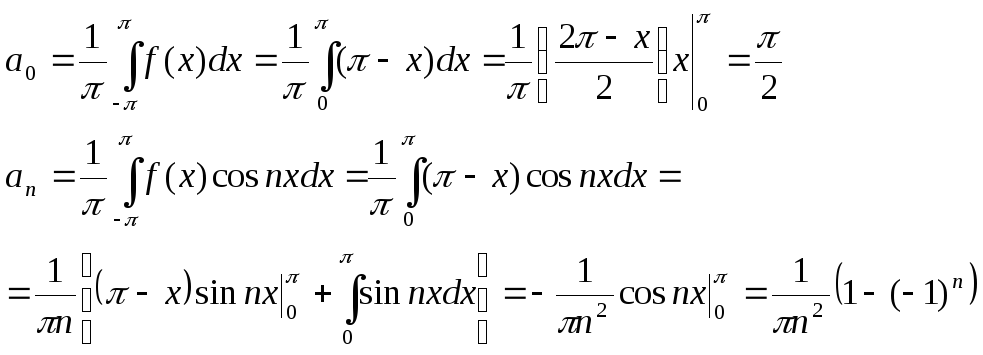
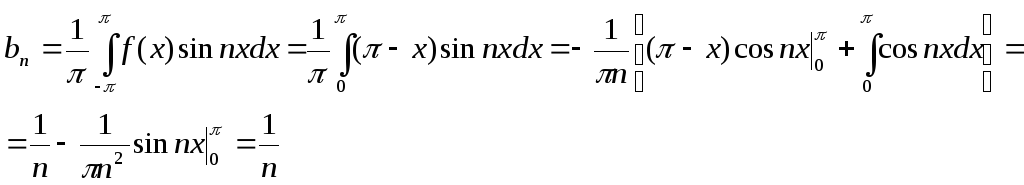
![]()
![]()
![]()
![]()
![]()
Сумма ряда
![]() :
1) в точках непрерывности:
:
1) в точках непрерывности:
![]()
2)
в точках разрыва:
![]() .
.
![]()
2) Разложить в ряд Фурье по синусам функцию, определенную на заданном интервале.
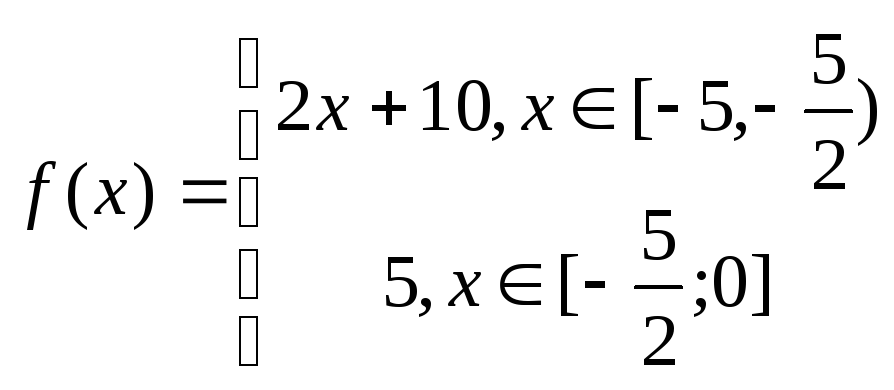
Продолжим функцию
нечетным образом до периода
![]() :
:
![]()

![]()
![]()
![]()
![]()
![]()
Сумма ряда
![]() :
1) в точках непрерывности:
:
1) в точках непрерывности:
![]()
2)
в точках разрыва:
![]() .
.
![]()
Вариант 12
3) Решить задачу
Штурма – Лиувилля.
Найти собственные функции, проверить
их ортогональность. Разложить функцию
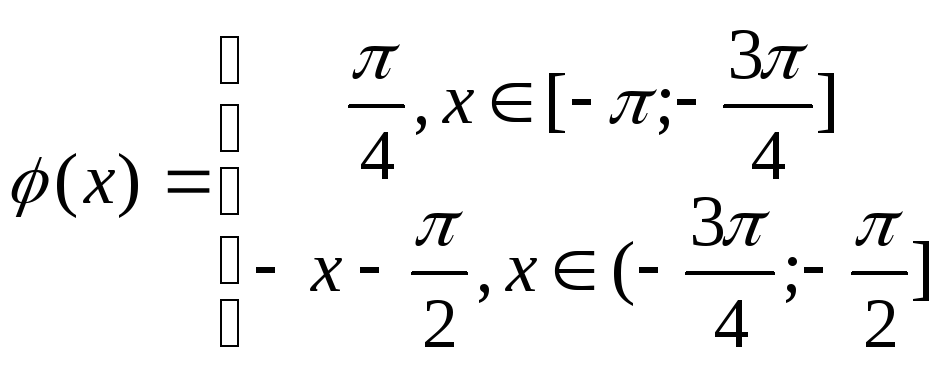 в ряд по собственным функциям.
в ряд по собственным функциям.
Задача
Штурма – Лиувилля для y(x):
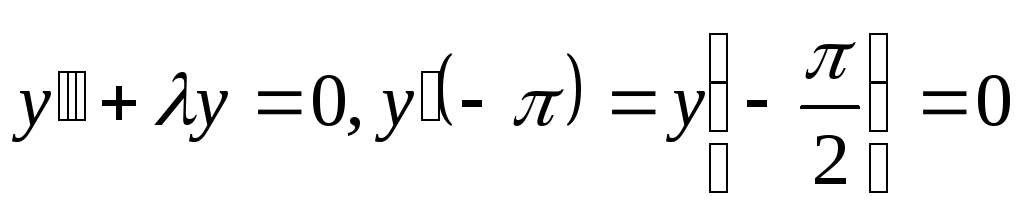 .
.
Решение ищем в
виде:
![]()
Характеристическое
уравнение
![]()
1)![]() - кратный корень.
- кратный корень.
Общее решение
имеет вид:
![]() ,
,
![]()
Граничные условия:
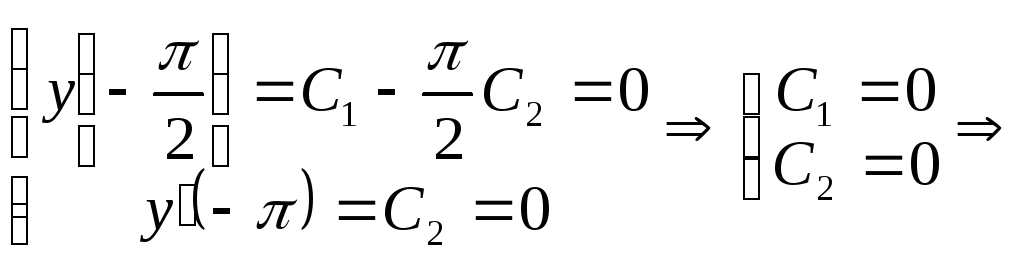
![]()
2)
![]()
![]()
Общее решение
имеет вид:
![]() Граничные условия:
Граничные условия:
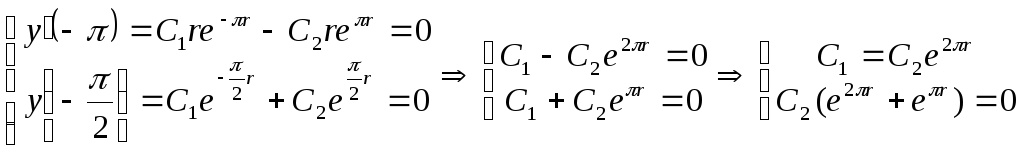
Т.к.
![]() - тривиальное решение.
- тривиальное решение.
3)![]()
![]()
Общее решение
имеет вид:
![]() Граничные условия:
Граничные условия:

![]() ;
;
![]()
Система собственных
функций
![]()
![]() .
.
Проверка на
ортогональность собственных функций
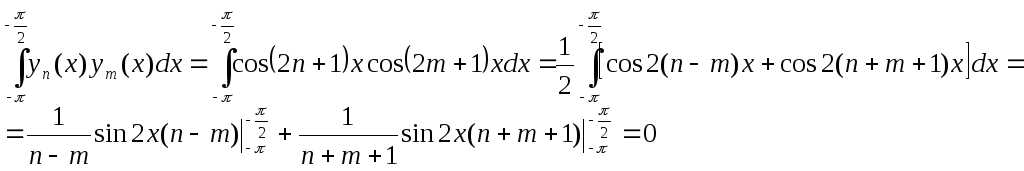
Система собственных
функций
![]() ортогональна.
ортогональна.
Разложим
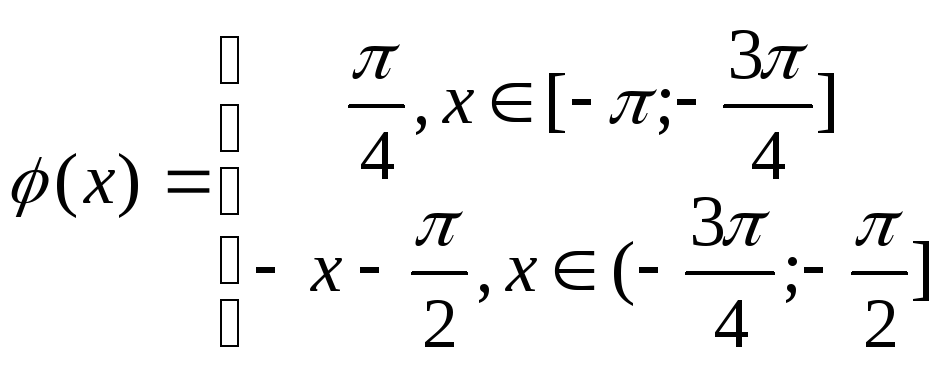 в ряд по собственным функциям
в ряд по собственным функциям
![]() :
:
Согласно теореме
Стеклова функцию можно разложить в ряд
Фурье:
![]() ,
,
где
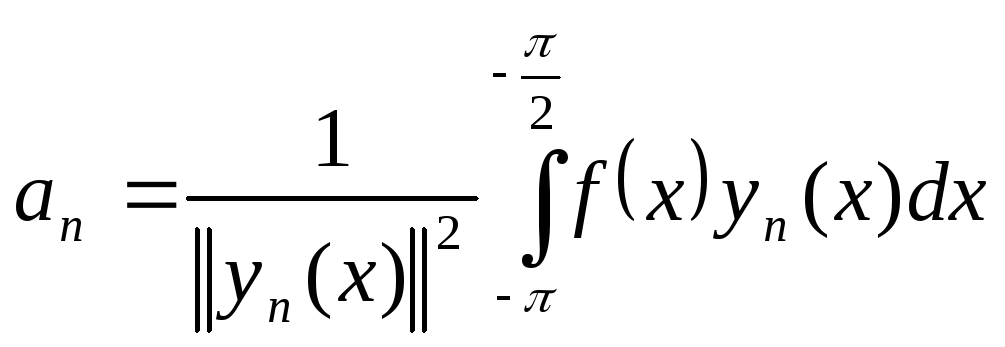
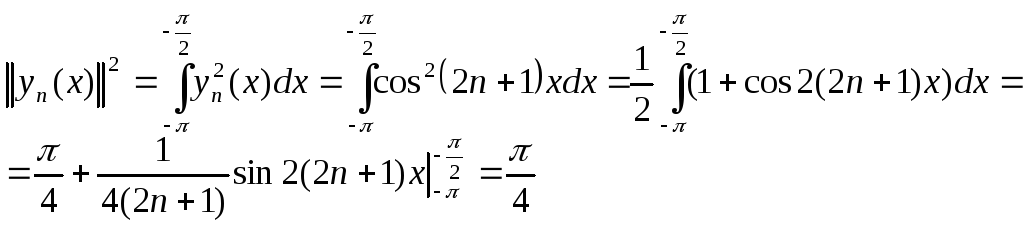

Значит
![]()
Вариант № 12
4) Решить задачу
о свободном колебании струны длины
![]() м с заданными краевыми условиями
м с заданными краевыми условиями
![]() ;
;
![]() .
Вычислить приближённое отклонение
середины струны при
.
Вычислить приближённое отклонение
середины струны при
![]() сек, используя для этого первые три
ненулевых слагаемых в разложении в ряд
функции
сек, используя для этого первые три
ненулевых слагаемых в разложении в ряд
функции
![]() .
Положить
.
Положить
![]() .
.
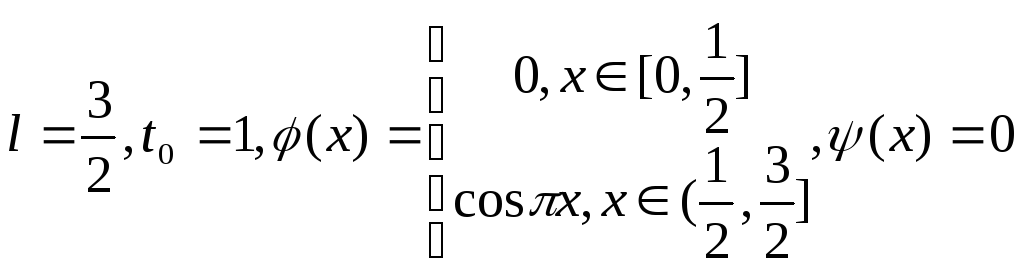
Решение
Будем искать
решение уравнения свободных колебаний
струны
![]() ,
удовлетворяющее однородным граничным
условиям:
,
удовлетворяющее однородным граничным
условиям:
![]() и начальным условиям
и начальным условиям
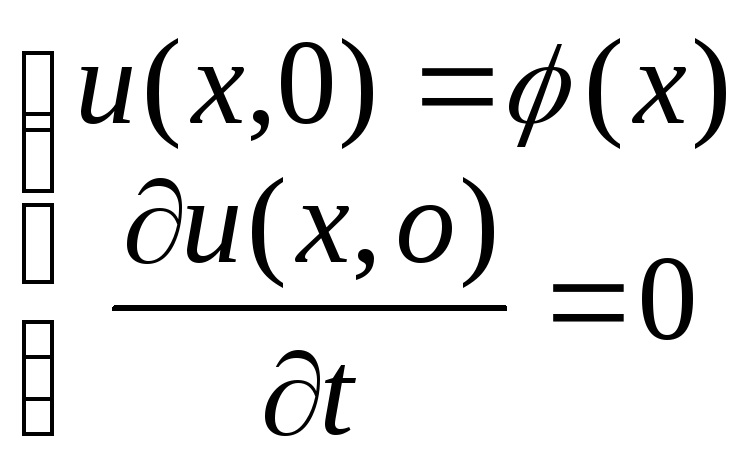 ,
представимое в виде произведения
,
представимое в виде произведения![]() .
.
Подставляем его
в исходное уравнение
![]()
Отсюда
![]()
Следовательно:
![]() Граничные условия
Граничные условия

При![]() имеем задачу Штурма – Лиувилля для
X(x):
имеем задачу Штурма – Лиувилля для
X(x):
![]() .
.
Решение ищем в
виде:
![]() Характеристическое уравнение
Характеристическое уравнение
![]()
1)![]() - кратный корень.
- кратный корень.
Общее решение
имеет вид:
![]()
Граничные условия:
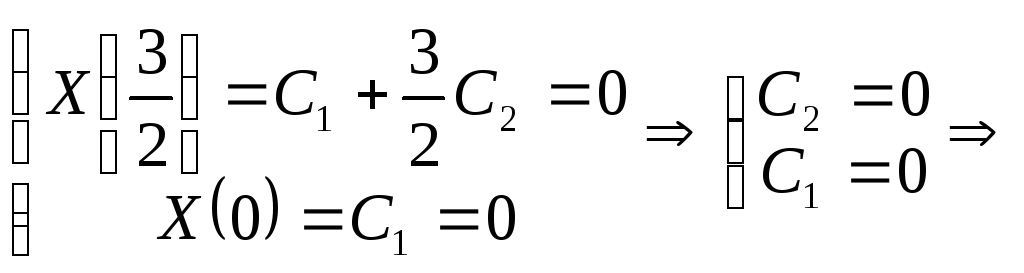
![]()
2)
![]()
![]() ,
где
,
где
![]() -
действительное число
-
действительное число
Общее решение
имеет вид:
![]()
Граничные условия:
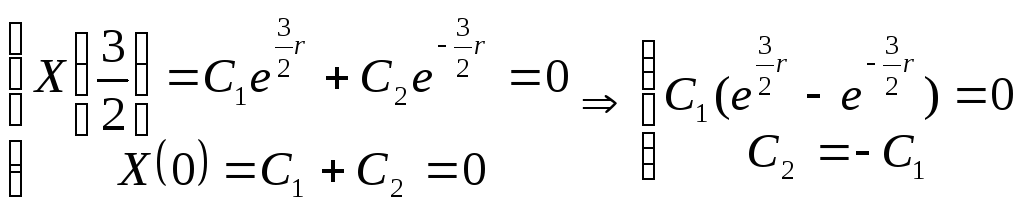
Т.к.
![]()
3)![]()
![]() ,
,
![]() -
действительное число
-
действительное число
Общее решение
имеет вид:
![]()
Граничные условия:
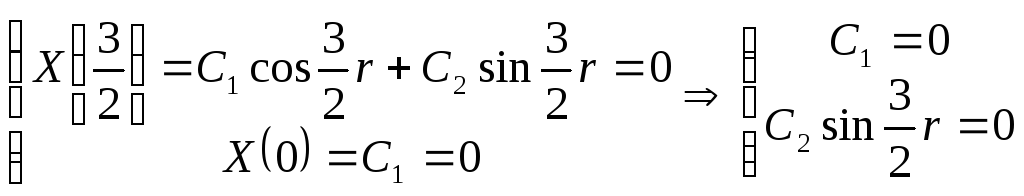
Если
![]()
При этом пусть
С2=1,
тогда
![]() ,
при
,
при
![]() .
.
Этим же значениям
![]() соответствуют решения уравнения
соответствуют решения уравнения
![]() ,
имеющие вид:
,
имеющие вид:
![]()
Частное решение уравнения свободных колебаний струны:
![]()
Общее решение имеет вид:
![]()
Начальные условия
 Значит
Значит
![]()
Разлагаем
![]() в ряд Фурье по синусам на промежутке
в ряд Фурье по синусам на промежутке
![]() :
:
![]() Сравнивая ряды, видим:
Сравнивая ряды, видим:

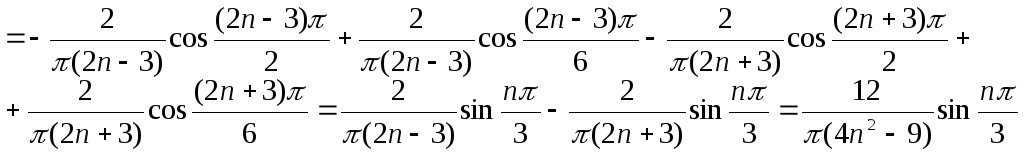
Общее решение представится в виде:
![]()
Приближённое
отклонение середины струны
![]() в
момент времени to
=1:
в
момент времени to
=1:
![]()
![]()
![]()
![]()
![]()
![]()
Вариант № 12
Вывести уравнение теплопроводности для тонкого ограниченного стержня, боковая поверхность которого теплоизолирована: сформулировать возможные типы краевых условий.
Определить температуру в произвольной точке х стержня в произвольный момент времени t - функцию u(x,t) в общем виде, при заданных краевых условиях, если начальные условия заданы функцией u(x,0) = f(x); решить задачу для заданной функции f(x); определить приближенно температуру стержня в точке xo в момент времени to (мин.), взяв три первых ненулевых члена ряда Фурье.
Типы краевых условий:
а) концы стержня
теплоизолированы ,т.е.
![]() ,
,
б) левый конец стержня теплоизолирован, а правый поддерживается при нулевой
температуре,
т.е.
![]()
в) правый конец стержня теплоизолирован, а левый поддерживается при нулевой
температуре,
т.е.![]() ,
,
![]() .
.
Коэффициент а2 температуропроводности: медь - 11.2 ∙ 10-5;
сталь - 1.27 ∙ 10-5;
алюминий - 8.80 ∙ 10-5.
Условия задачи
f(x)
=
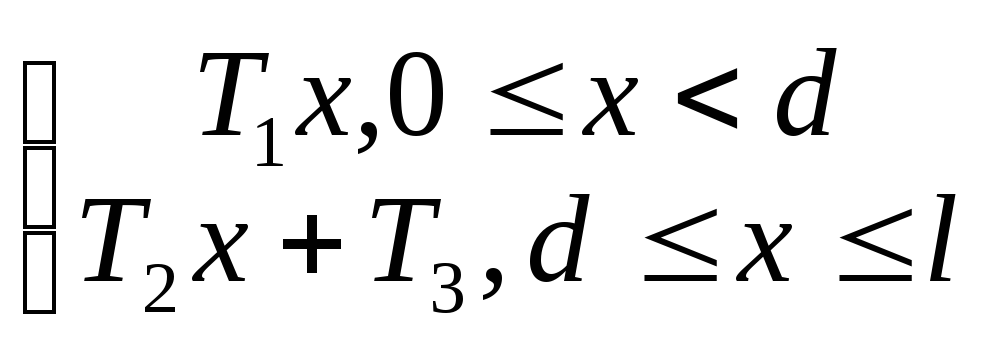 ,
,
![]()
![]() ,
,
f(d)
=
![]() ,т.е.
x=d
точка разрыва
,т.е.
x=d
точка разрыва
тип краевых условий – в
материал- алюминий
xo
=
![]() , to
= 50
, to
= 50
Решение
Ищем решение
уравнения теплопроводности
![]()
![]() с начальным условием:
с начальным условием:
u(x,0)
= f(x)
=
 и граничными условиями:
и граничными условиями:
![]() в виде
u(x,t)
= X(x)T(t).
в виде
u(x,t)
= X(x)T(t).
Подставляем его в исходное уравнение X(x)T′(t) = а2 X″(x)T(t).
Отсюда
![]()
Следовательно:
![]() Граничные условия
Граничные условия
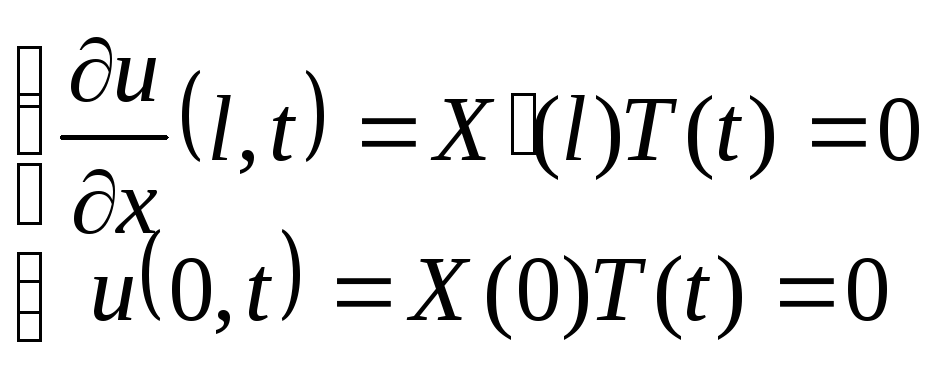
При
![]() имеем
задачу Штурма – Лиувилля для X(x):
имеем
задачу Штурма – Лиувилля для X(x):
![]() .
.
Решение ищем в
виде:
![]()
Характеристическое
уравнение
![]()
1)![]() - кратный корень.
- кратный корень.
Общее решение
имеет вид:
![]()
Граничные условия:
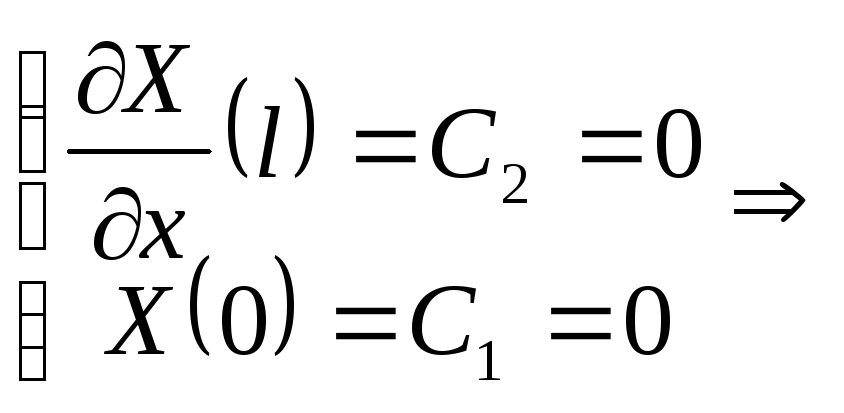
![]() - тривиальное решение
- тривиальное решение
2)
![]()
![]() ,
где
,
где
![]() -
действительное число
-
действительное число
Общее решение
имеет вид:
![]()
Граничные условия:
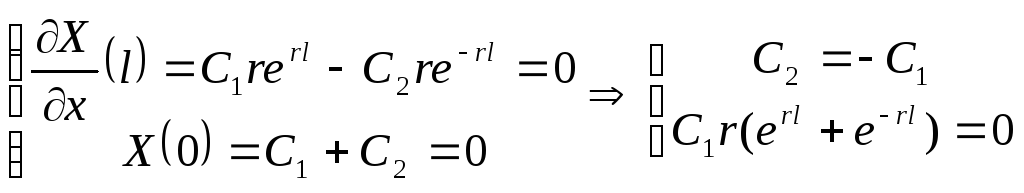
Т.к.
![]() - тривиальное решение.
- тривиальное решение.
3)![]()
![]() ,
,
![]() -
действительное число
-
действительное число
Общее решение
имеет вид:
![]()
Граничные условия:
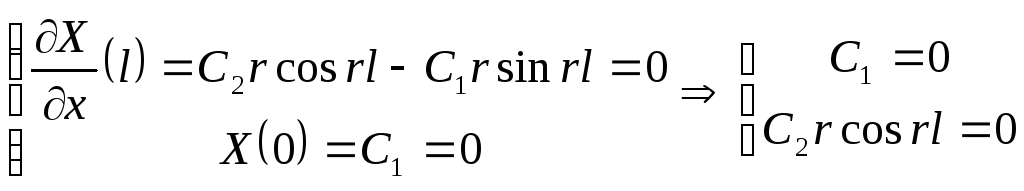
Если
![]()
При этом пусть
С1=1,
тогда
![]() ,
при
,
при
![]() .
.
Этим же значениям
![]() соответствуют решения уравнения
соответствуют решения уравнения
![]() , имеющие вид:
, имеющие вид:
![]()
Частное решение уравнения теплопроводности:
![]()
Общее решение имеет вид:
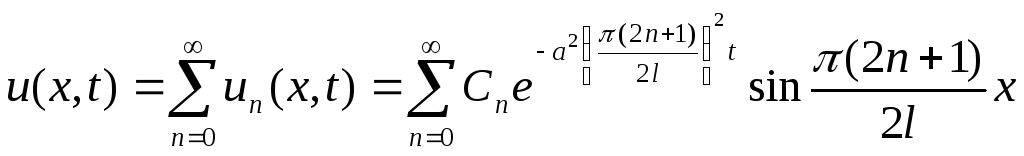
Начальные условия
![]() =
=
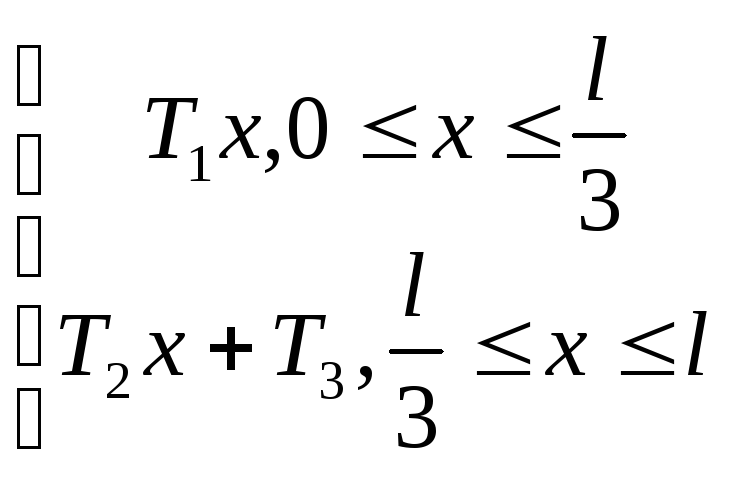
Разлагаем f(x)
в ряд по собственным функциям
![]() :
:
![]()
Сравнивая ряды, видим:
 Общее
решение представится в виде:
Общее
решение представится в виде:
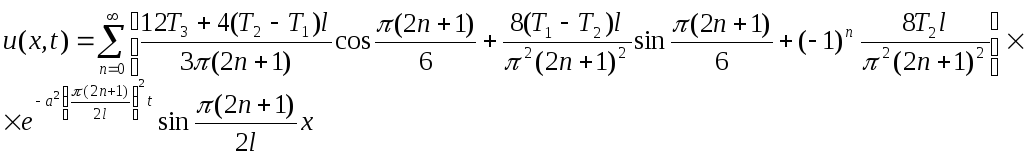
Приближённое
значение температуры стержня в точке
xo
=
![]() в момент времени to
= 50:
в момент времени to
= 50: