38. Сопряжённый оператор

Свойствособственныхвекторовсамосопряженногооператора

Предложение о собственных векторах самосопряженного оператора

Если A самосопряженный линейный оператор в евклидовом пространстве, то собственные векторы оператора A, относящиеся к его различным собственным значениям, ортогональны.

Доказательство. Пусть X и Y собственные векторы оператора A, относящиеся к его различным собственным значениям λ1 и λ2 соответственно. Тогда

A(X) · Y = (λ1X)Y = λ1(XY) и X · A(Y) = X(λ2Y) = λ2(XY).

Поскольку оператор A самосопряжен, A(X) · Y = X · A(Y). Следовательно, λ1(XY) = λ2(XY), т. е. (λ1 − λ2)(XY) = 0. Поскольку λ1 − λ2 6= 0, мы получаем, что XY = 0.

§ 38. Сопряженный оператор

Матрицасамосопряженногооператора(1)

Определение

Квадратная матрица над полем C называется эрмитовой, если A = A .

Предложение о матрице самосопряженного оператора

Для линейного оператора A в пространстве V со скалярным произведением следующие условия эквивалентны:

1)A самосопряженный оператор;

2)матрица оператора A в любом ортонормированном базисе эрмитова;

3)матрица оператора A в некотором ортонормированном базисе

эрмитова.

Доказательство. Импликация 1) = 2) вытекает из следствия о матрице сопряженного оператора в ортонормированном базисе, а импликация 2) = 3) очевидна.

§ 38. Сопряженный оператор

Матрицасамосопряженногооператора(2)

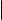
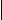
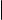
3) = 1) Обозначим через P тот ортонормированный базис, в котором матрица оператора A эрмитова. Пусть X, Y V . Рассуждая так же, как в доказательстве предложения о матрице сопряженного оператора, но учитывая, что матрица Грама базиса P единична, получаем, что

A(X) · Y = [X]P · A · [Y]P , а X · A(Y) = [X]P · A · [Y]P .

Поскольку, по условию, A = A , получаем, что

A = A = A = A .

Следовательно, A(X) · Y = X · A(Y). Поскольку это выполнено для любых векторов X, Y V , получаем, что A = A .

§ 38. Сопряженный оператор

Свойствасамосопряженногооператора(1)

Лемма о свойствах самосопряженного оператора

Если A самосопряженный линейный оператор в пространстве V со скалярным произведением, то:

1)все собственные значения оператора A являются действительными числами;

2)если λ собственное значение оператора A, то

Im(A − λE) ∩ Ker(A − λE) = {0};

3)всякое корневое подпространство пространства V относительно оператора A имеет глубину 1.

Доказательство. 1) Пусть λ собственное значение оператора A. Тогда

2

A(λX) · X = λA(X) · X = λ A(X) · X = λ(λX · X) = λ (XX) и (λX) · A(X) = (λX)(λX) = λλ(XX).

Поскольку оператор A самосопряжен, A(λX) · X = (λX) · A(X), и потому

λ2(XX) = λλ(XX), т. е. (λ2 − λλ)(XX) = 0. Вектор X является собственным, и потому X =6 0. Следовательно, λ2 = λλ. Это означает, что либо λ = 0, либо λ = λ. В обоих случаях λ R.

§ 38. Сопряженный оператор

Свойствасамосопряженногооператора(2)

2) Поскольку Ker(A − λE) ∩ Ker(A − λE) = {0}, достаточно доказать, что Im(A − λE) Ker(A − λE) . Пусть X Im(A − λE) и

Y Ker(A − λE). Из последнего включения вытекает, что (A − λE)(Y) = 0, т. е. A(Y) = λY. Требуется доказать, что XY = 0. Существует вектор Z такой, что X = (A − λE)(Z) = A(Z) − λZ. Используя, что оператор A самосопряжен, а λ = λ (в силу п. 1) доказываемого утверждения), имеем

XY = A(Z) − λZ Y = A(Z) · Y − (λZ)Y = Z · A(Y) − λ(ZY) =

=Z(λY) − λ(ZY) = λ(ZY) − λ(ZY) = λ(ZY) − λ(ZY) = 0.

3)Требуется доказать, что если λ собственное значение оператора A,

2

то Ker(A − λE) = Ker (A − λE) . Сначала проверим, что

2

Ker(A − λE) Ker (A − λE) . Если X Ker(A − λE), то (A − λE)(X) = 0. Но тогда (A − λE)2 (X) = (A − λE) (A − λE)(X) = (A − λE)(0) = 0, и потому X Ker (A − λE)2 . Осталось проверить, что

Ker (A − λE)2 Ker(A − λE). Пусть X Ker (A − λE)2 . Положим Y = (A − λE(X). Ясно, что Y Im(A − λE). С другой стороны,

(A − λE)(Y) = (A − λE)2(X) = 0, и потому Y Ker(A − λE). Таким образом, Y Im(A − λE) ∩ Ker(A − λE). Учитывая п. 2) доказываемого утверждения, получаем, что Y = 0. Поскольку Y = (A − λE)(X), это означает, что X Ker(A − λE). Тем самым, включение

Ker (A − λE)2 Ker(A − λE) доказано.

§ 38. Сопряженный оператор

Свойствоэрмитовыхматриц

Определение

Квадратная матрица A называется симметрической, если A = A .

Очевидно, что квадратная матрица над полем R эрмитова тогда и только тогда, когда она является симметрической матрицей.

1-е следствие об эрмитовых матрицах

Все корни характеристического многочлена произвольной эрмитовой матрицы, в частности, произвольной симметрической матрицы над полем R, являются действительными числами.

Доказательство. Пусть A квадратная эрмитова матрица, а A линейный оператор в пространстве CN , матрицей которого в стандартном базисе этого пространства является матрица A. Поскольку стандартный базис ортонормирован, из предложения о матрице самосопряженного оператора вытекает, что оператор A является самосопряженным. Из п. 2) леммы о свойствах самосопряженного оператора вытекает, что все собственные значения оператора A, т. е. все корни характеристического многочлена матрицы A, являются действительными числами.

§ 38. Сопряженный оператор

Основнаятеоремаосамосопряженномоператоре(1)

Основная теорема о самосопряженном операторе

Линейный оператор A в пространстве V со скалярным произведением является самосопряженным тогда и только тогда, когда в V существует ортонормированный базис, состоящий из собственных векторов оператора A и все корни характеристического многочлена этого оператора являются действительными числами.

Доказательство. Достаточность. Если существует ортонормированный базис, состоящий из собственных векторов оператора A и все корни характеристического многочлена этого оператора являются действительными числами, то матрица A оператора A в этом базисе диагональна, и на ее диагонали стоят действительные числа (см. критерий приводимости оператора к диагональному виду и доказательство этого утверждения в § 33). Ясно, что A = A . Из предложения о матрице самосопряженного оператора вытекает, что оператор A является самосопряженным.

§ 38. Сопряженный оператор

Основнаятеоремаосамосопряженномоператоре(2)

Необходимость. Сначала докажем, что характеристический многочлен оператора A разложим на линейные множители. Если V унитарно, это вытекает из основной теоремы высшей алгебры. Если же V евклидово, обозначим через A матрицу оператора A в некотором ортонормированном базисе. В силу предложения о матрице самосопряженного оператора A симметрическая матрица над R. Из следствия об эрмитовых матрицах вытекает теперь, что все корни характеристического многочлена матрицы A, а значит и оператора A, являются действительными числами. Следовательно, многочлен χA разложим на линейные множители над полем R, что и требовалось доказать в рассматриваемом случае.

Итак, многочлен χA разложим на линейные множители. Согласно теореме о корневом разложении (см. § 35), пространство V является прямой суммой корневых подпространств относительно A. При этом из п. 3) леммы о свойствах самосопряженного оператора вытекает, что всякое корневое подпространство имеет вид Ker(A − λE) для некоторого собственного значения λ оператора A. Если X Ker(A − λE), то

(A − λE)(X) = 0, откуда A(X) = λX. Таким образом, все ненулевые векторы во всех корневых подпространствах являются собственными векторами оператора A.

§ 38. Сопряженный оператор

Основнаятеоремаосамосопряженномоператоре(3)

Взяв в каждом из корневых подпространств ортонормированный базис и объединив все эти базисы, мы получим базис всего пространства, состоящий из собственных векторов оператора A. В силу предложения о собственных векторах самосопряженного оператора этот базис ортонормирован. Остается учесть, что все корни характеристического многочлена этого оператора являются действительными числами в силу п. 1) леммы о свойствах самосопряженного оператора.

§ 38. Сопряженный оператор

Унитарныематрицы

Определение

Квадратная матрица A над полем C называется унитарной, если

AA = A A = E .

Ясно, что если матрица A унитарна, то она обратима и A−1 = A .

Предложение о матрицах перехода в унитарном пространстве

Матрица перехода от одного ортонормированного базиса к другому ортонормированному базису в унитарном пространстве является унитарной.

Доказательство. Пусть V унитарное пространство, P = {P1 , P2 , . . . , PN } и Q = {Q1 , Q2, . . . , QN } его ортонормированные базисы и T = (tI j) матрица перехода от P к Q. По определению матрицы перехода произведение i-й строки матрицы T на j-й столбец матрицы T равен скалярному произведению векторов QI и QJ . Поскольку базис Q ортонормирован, это означает, что T · T = E . Следовательно,

E = E = T · T = T · T = T · T = T T . Аналогично проверяется, что

TT = E .

§ 38. Сопряженный оператор