
- •Вопрос 1. Первообразная и ее общий вид
- •Вопрос 2. Свойства неопределенного интеграла
- •Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
- •Вопрос 4. Интегрирование по частям неопределенного интеграла
- •Вопрос 5. Необходимое условие интегрируемости функции.
- •Вопрос 6. Суммы Дарбу и их свойства.
- •Вопрос 7. Лемма Дарбу-Римана.
- •Вопрос 8. Критерий интегрируемости
- •Вопрос 9.Свойства интеграла Римана
- •Вопрос 10.Интегрируемость непрерывной функции
- •Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
- •Вопрос 12. Интегрируемость функции, монотонной на отрезке.
- •Вопрос 13. Теоремы о среднем для интеграла.
- •Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
- •Вопрос 15. Формула Ньютона-Лейбница и её обобщение.
- •Вопрос 16. Интегрирование заменой переменной и по частям в определённом интеграле
- •Вопрос 17. Векторные пространство Rm, скалярные произведения, модуль, расстояние.
- •Вопрос 18. Критерии замкнутости в метрическом пространстве.
- •1 Критерий замкнутости
- •2 Критерий замкнутости
- •Вопрос 19. Свойство компактности в метрическом пространстве.
- •Вопрос 20. Компактность m-мерного отрезка.
- •Вопрос 21. Критерий компактности в Rm.
- •Вопрос 22. Критерий Коши и покоординатная сходимость.
- •Вопрос 23. Теорема Больцано-Вейерштрасса
- •Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
- •Вопрос 25. Повторные и двойные пределы.
- •26. Непрерывность сложной функции многих переменных.
- •27. Теорема Коши о промежуточном значении функции.
- •28. Теоремы Вейерштрасса для функций многих переменных.
- •29. Дифференцируемость функции многих переменных, вид нелинейной части.
Вопрос 10.Интегрируемость непрерывной функции
Теорема. Если функцийfнепрерывна на отрезке [a,b] то она интегрируема на этом отрезке
Доказательство:
В силу
теоремы Кантора функция fравномерно непрерывна на [a,b].Возьмем
произвольное𝜀>0,
тогда из равномерной непрерывности
функцииfна [a,b]
следует, что для любыхx’,x’’𝜖[a,b],
удовлетворяющих условию |x’-x’’|<𝛿выполняется |f(x’)-f(x’’)|<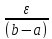 .
.
Если взять разбиение Т такое, что 𝜆(T)<𝛿, ввиду того, что
𝜔(f(x),[xk,xk+1])=𝜔k(f)<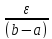
Имеем
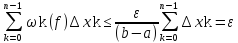
Следовательно, по критерию интегрируемости (критерий Римана)
Функция fинтегрируема на отрезке [a,b]
Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
Если f – ограничена на [a,b] и имеет конечное число точек разрыва, то f интегрируема на [a,b]
Доказательство.
Не уменьшая общности, можно считать,
что у функции f
на отрезке [a,b]
лишь одна точка разрыва и этой точкой
является a
(см. рис. 9.6.1). Докажем, что для этой
функции выполняется критерий
интегрируемости Римана. Возьмем любое
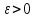 ,
выберем точку
,
выберем точку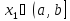 такую, чтобы
такую, чтобы
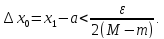
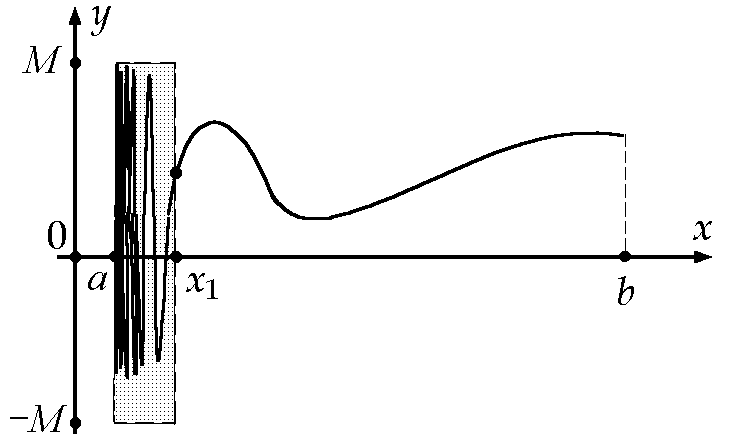
Рис. 9.6.1
На отрезке [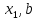 ]
функцияf
интегрируема как непрерывная,
следовательно, по критерию интегрируемости,
по заданному
]
функцияf
интегрируема как непрерывная,
следовательно, по критерию интегрируемости,
по заданному
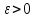 найдётся разбиение
найдётся разбиение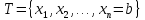 отрезка [
отрезка [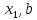 ],
при котором
],
при котором

Если
теперь рассмотреть разбиение
 отрезка
[a,b],
то в силу (рис. 9.6.1) и (рис. 9.6.2)
отрезка
[a,b],
то в силу (рис. 9.6.1) и (рис. 9.6.2)
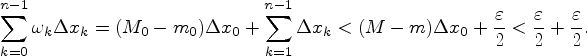
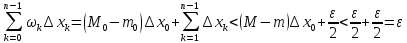
Следовательно, по критерию интегрируемости, функция f интегрируема на [a,b].
Вопрос 12. Интегрируемость функции, монотонной на отрезке.
Если f – монотонна на [a,b], f – интегрируема на [a,b].
Доказательство.
Пусть функция f
монотонно возрастает на [a,b]
и
 .
Возьмем любое
.
Возьмем любое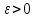 и разбиениеT
отрезка [a,b],
от которого потребуем, чтобы его мелкость
и разбиениеT
отрезка [a,b],
от которого потребуем, чтобы его мелкость
 .
Из монотонностиf
следует, что
.
Из монотонностиf
следует, что
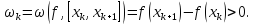
Следовательно,
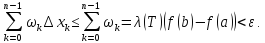
Отсюда, по критерию интегрируемости, функция f интегрируема на [a,b].
Вопрос 13. Теоремы о среднем для интеграла.
Теорема 1. Пусть
функции f
и g
интегрируемы на отрезке [a,b],
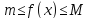 на [a,b],
на [a,b],
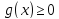 на [a,b].
Тогда
на [a,b].
Тогда
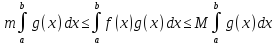
Доказательство.
По свойству 6 интеграла функция fg
интегрируема на отрезке [a,b].
Умножая неравенство
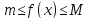 на
на ,
получим
,
получим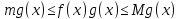
Интегрируя его по отрезку [a,b], используя свойства интеграла, получим требуемое неравенство.
Следствие.
Пусть функция
f
интегрируема на отрезке [a,b]и
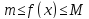 на [a,b].
Тогда
на [a,b].
Тогда
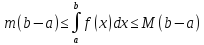
Доказательство.
В теореме 1
нужно взять
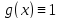 .
.
Теорема 2.
Пусть функция
f
непрерывна на отрезке [a,b],
функция
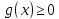 интегрируема на отрезке [a,b].
Тогда существует
интегрируема на отрезке [a,b].
Тогда существует
 такое, что выполняется
такое, что выполняется
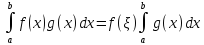
Доказательство.
Так как функция f
непрерывна на отрезке [a,b],
то у нее существуют
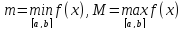 (см. рис. 9.8.1). В силу предыдущей теоремы
имеют место неравенства
(см. рис. 9.8.1). В силу предыдущей теоремы
имеют место неравенства
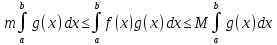
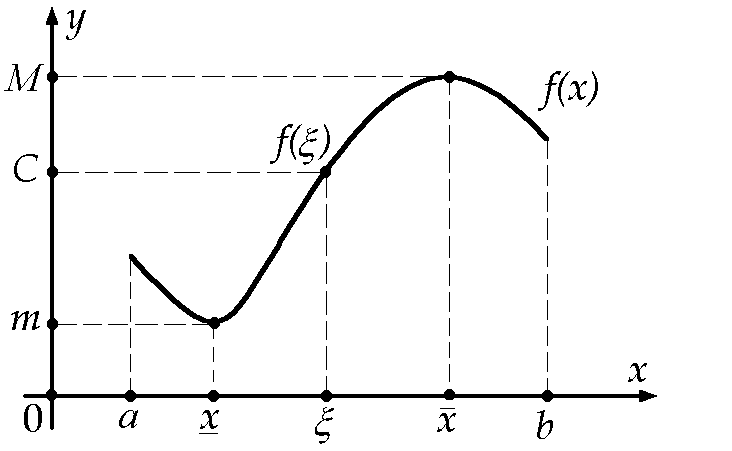
Рис. 9.8.1
Если интеграл
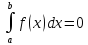 ,
то за ξ можно взять любую точку из отрезка
[a,b]
и
,
то за ξ можно взять любую точку из отрезка
[a,b]
и
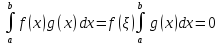
Если
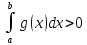 ,
то
,
то
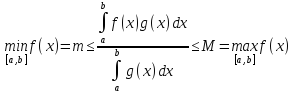
Таким образом,
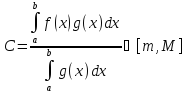
В
силу теоремы Коши о промежуточных
значениях существует
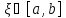 такое, что
такое, что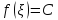 .
Отсюда получаем требуемое равенство.
.
Отсюда получаем требуемое равенство.
Следствие.
Пусть функция
f
непрерывна на отрезке [a,b].
Тогда существует
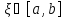 такое,
что
такое,
что
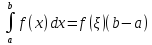
Доказательство.
В предыдущей теореме нужно положить
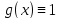 .
.
Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
Пусть функцияfинтегрируема на [a,b]. Функция

называется интегралом с переменным верхним пределом интегрирования.
Теорема 1.Пусть функцияf(t) интегрируема на отрезке [a,b]. Тогда интеграл с переменным верхним пределом интегрированияF(x) непрерывен на отрезке [a,b].
Доказательство.Так как функцияfинтегрируема на отрезке [a,b],
то она ограничена на нем, т. е. существует
число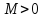 такое, что для всех
такое, что для всех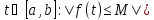 .
Пусть
.
Пусть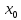 – любая точка из [a,b]и
ε > 0 – произвольное. Используя свойства
интеграла, получим
– любая точка из [a,b]и
ε > 0 – произвольное. Используя свойства
интеграла, получим
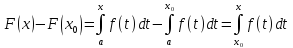
Следовательно,

Итак, для
заданного ε > 0 число
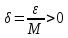 таково, что для всехxсо
свойством
таково, что для всехxсо
свойством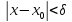

т. е. функция F(x) непрерывна в точкеx0.
Теорема 2.Если функцияfинтегрируема на отрезке [a,b]и
непрерывна в точке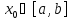 ,
то функцияFдифференцируема
в точке
,
то функцияFдифференцируема
в точке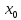 и
и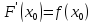
Доказательство.Ввиду непрерывности
функцииfв точке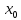 для любого
для любого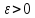 существует
существует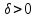 такое, что для всех
такое, что для всех выполняется
выполняется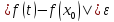 .
Тогда для любого
.
Тогда для любого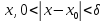 выполняется
выполняется
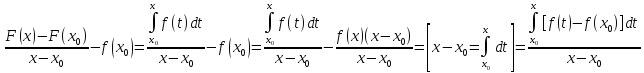
Итак,
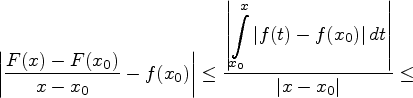
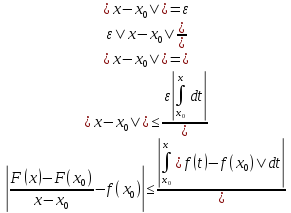
что, по
определению, означает дифференцируемость
функции F(x)
в точке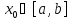 .
.
Теорема 3 (существование первообразной).Пусть функцияfнепрерывна на отрезке [a,b]. Тогда функция
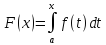
является первообразной для функции fна отрезке [a,b].
Доказательство.Изтеоремы 9.9.2следует, что
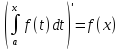
а это, по определению, означает, что F(x) является первообразной функцией дляf(x) на отрезке [a,b].
Теорема 4 (Ньютона - Лейбница).Если функция f непрерывна на отрезке [a,b]и Ф есть ее первообразная на этом отрезке, то имеет место формула
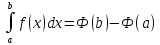
Таким образом, для вычисления определенного интеграла по отрезку [a,b] от непрерывной функцииfследует вычислить значения произвольной ее первообразной Ф в точкахbиaи вычесть из первого значения второе.
Доказательство.Изтеоремы
9.9.3следует, что функция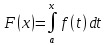 есть первообразная для функцииfна отрезке [a,b].
Следовательно, любая другая ее
первообразная Ф(x) имеет
вид
есть первообразная для функцииfна отрезке [a,b].
Следовательно, любая другая ее
первообразная Ф(x) имеет
вид
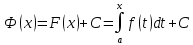
поэтому
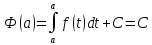

Отсюда следует требуемое равенство.
Полученная формула называется основной формулой интегрального исчисления, которую часто записывают в виде
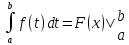
где введено обозначение
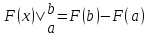
Эту теорему можно переформулировать следующим образом.
Теорема 5.Если функцияF(x) непрерывно дифференцируема на отрезке [a,b], то
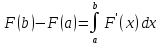
Для доказательства достаточно применить
теорему Ньютона - Лейбница к функции
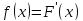 .
.
