V. 17. Последнее задание содержит задачи двух типов – составление и решение дифференциального уравнения на физическую и геометрическую тему. Рассмотрим оба типа задач.

а). В контур с индуктивностью с и сопротивлением включена сторонняя ЭДС . Определить зависимость тока от времени , если в начальный момент ток равен нулю.

Решение. Как известно, падение напряжения в обозначенном контуре (см. рисунок) складывается из падения его на сопротивлении и ЭДС самоиндукции . Таким образом, уравнение для тока в к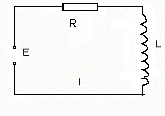онтуре запишется в виде

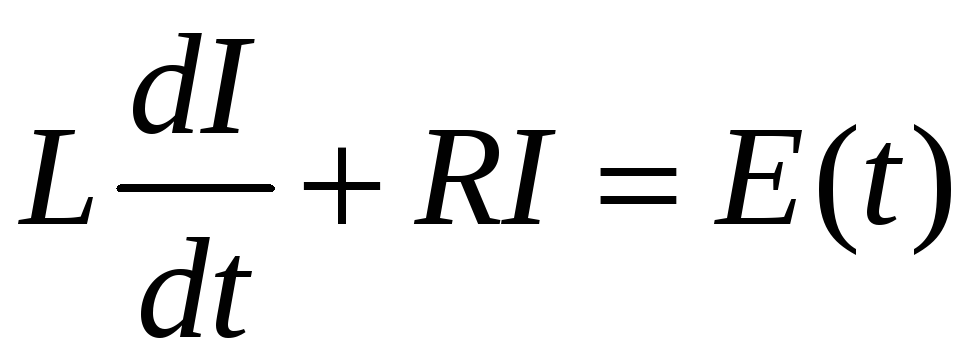, (1)

где – внешняя электродвижущая сила.

Запишем уравнение (1) в виде

(2)

где для краткости введено обозначение Получили неоднородное линейное дифференциальное уравнение 1-го порядка с постоянными коэффициентами. Решение его складывается из решения однородного уравнения 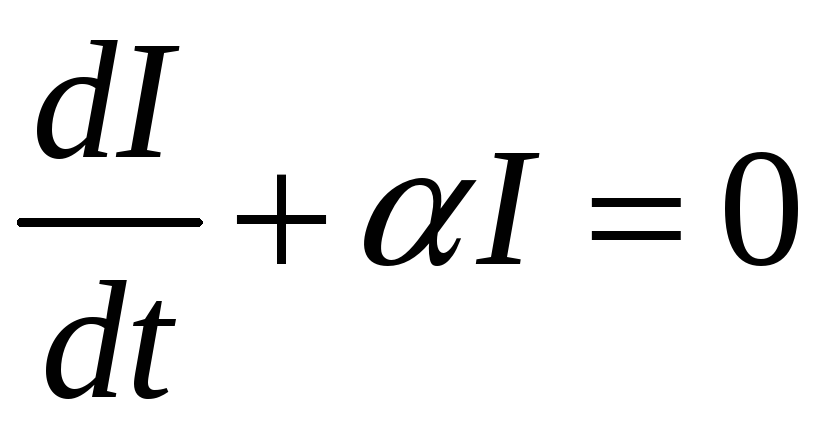, равного и частного решения неоднородного уравнения, которое ищем по виду правой части – . Подставляя его в (2), определяем константы 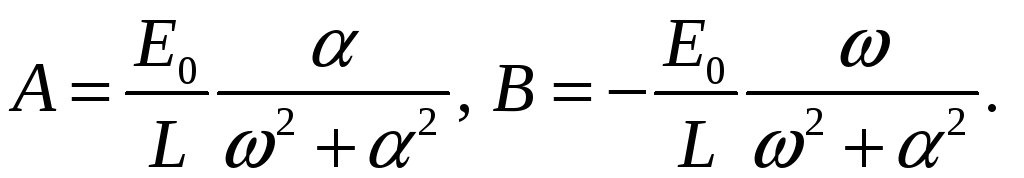Таким образом, частное решение имеет вид 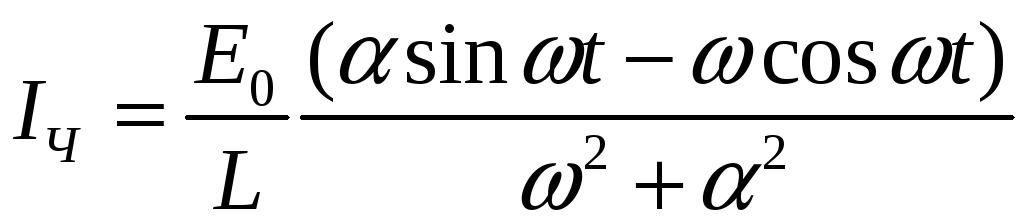. Его можно представить в другом виде, введя угол сдвига фазы φ тока в контуре по отношению к ЭДС. Для этого положим Постоянная отсюда равна 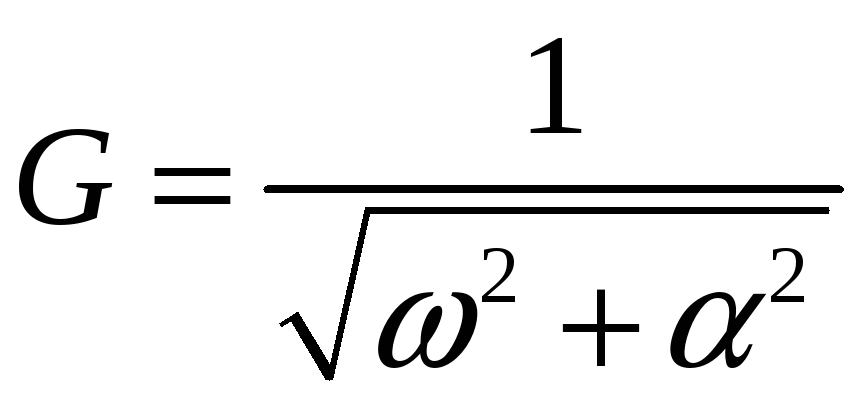, а частное решение теперь принимает вид 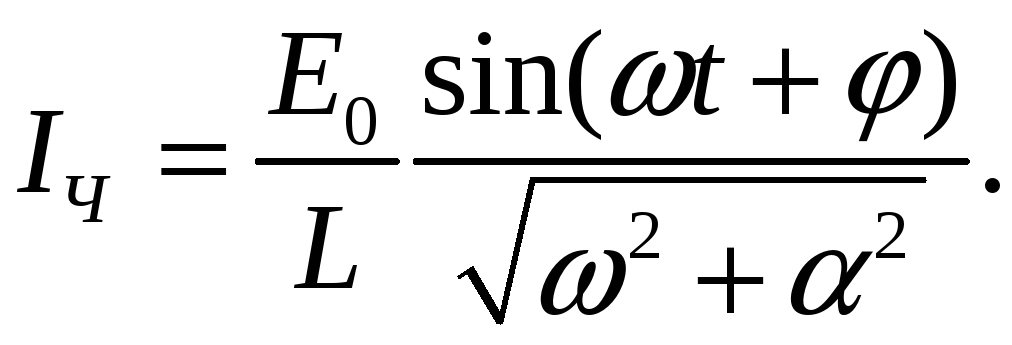Общее решение его запишется в виде

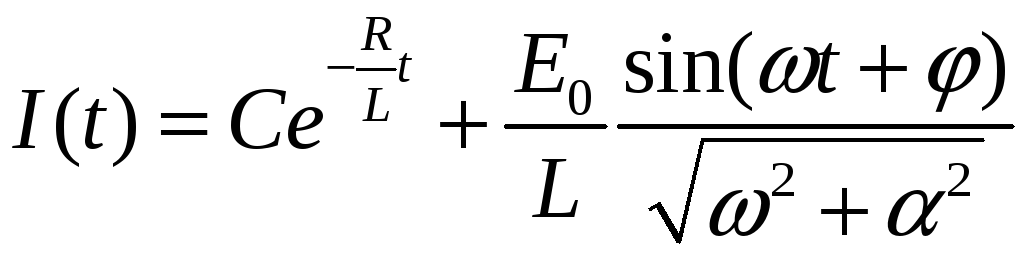. (3)

Постоянная С определяется из начального условия : .

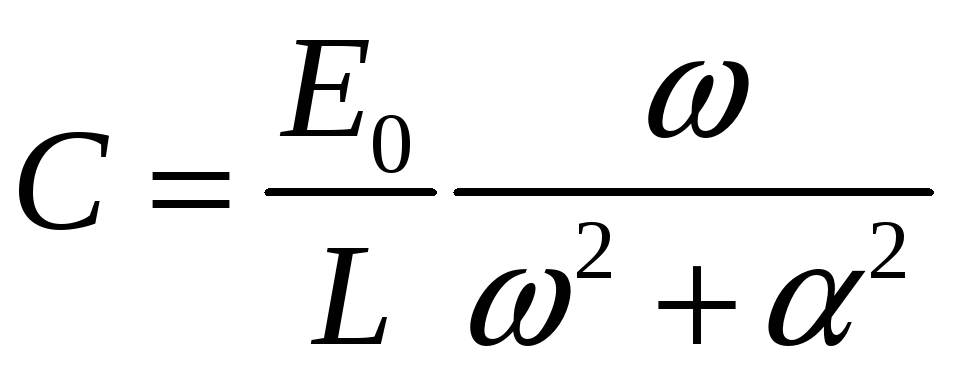Окончательно решение уравнения (2) запишется в виде

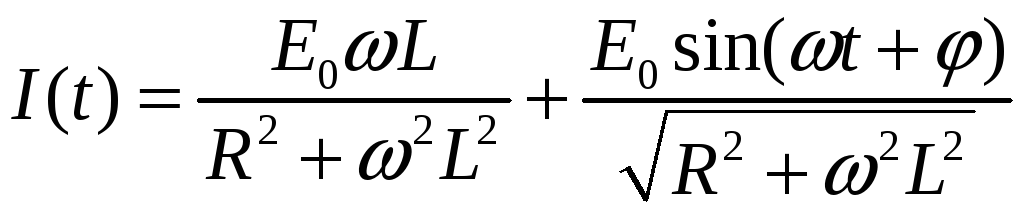(4)

Если достаточно велико, то – малая величина и ею в формуле (4) можно пренебречь (затухание собственного тока в

контуре за счёт активного сопротивления). Тогда будем иметь

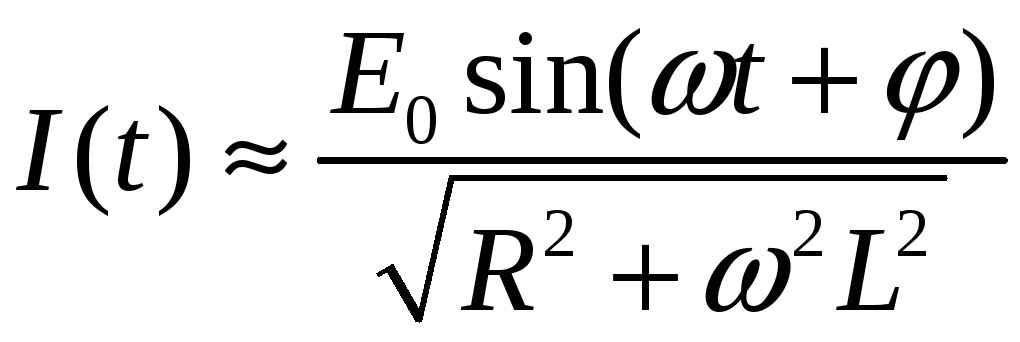(5)

Другой вариант нахождения частного решения

В правую часть уравнения (1) введём вместо комплексную величину: . Тогда выражение для тока становится также комплексным – , и, в силу линейности уравнения (1), искомый ток определяется как его мнимая часть: . Теперь решение уравнения

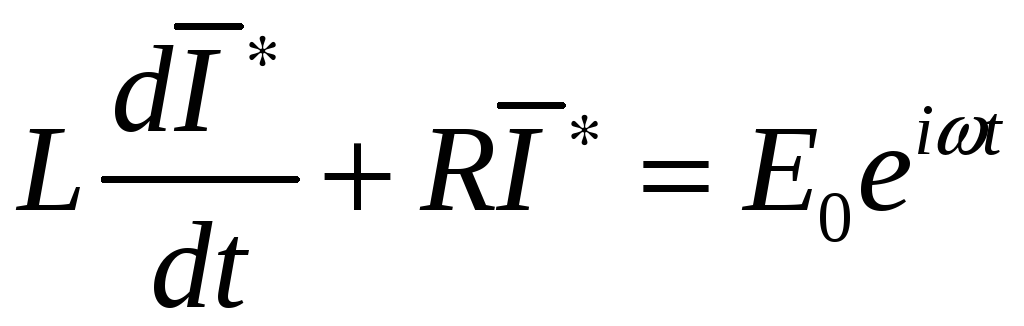(6) ищется в виде . Подставляя его в уравнение (6), получаем уравнение для , откуда 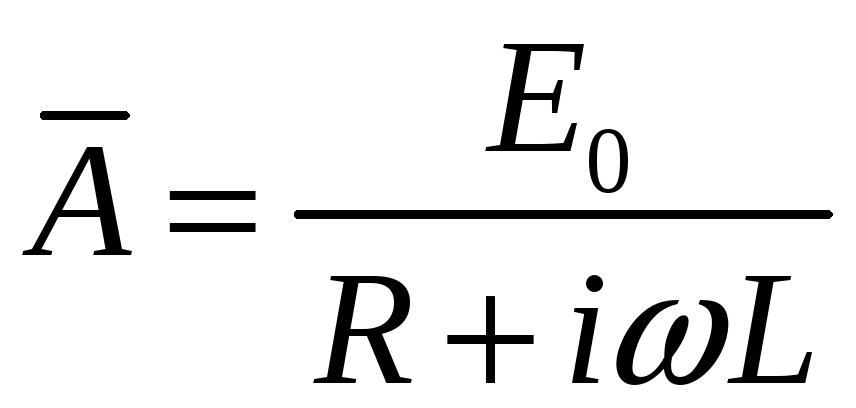, или в показательной форме 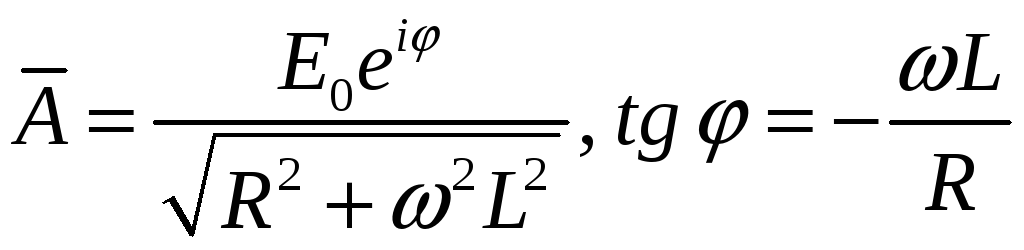. Таким образом, частное решение имеет вид 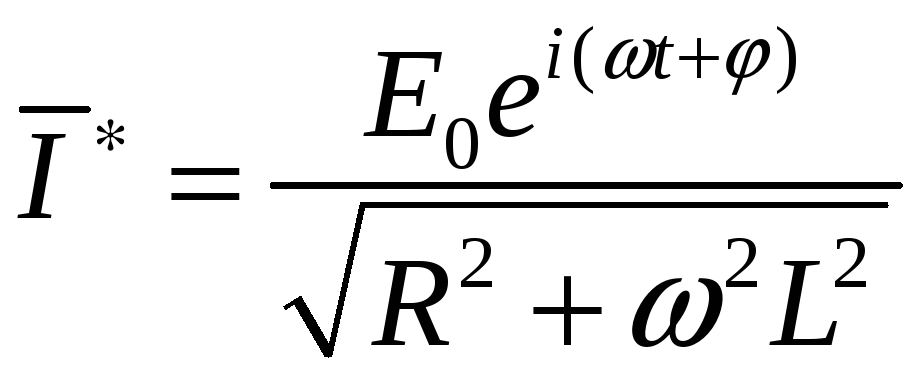, а его мнимая часть даёт то же выражение для тока, что и в (4).

Замечание. Решение уравнения (2) можно также получить с помощью метода Бернулли.

Ответ: .

б) Записать уравнение кривой, проходящей через точку , если известно, что площадь трапеции DMCO (см. рисунок), ограниченной осями координат, любой касательной к этой кривой в точке M(x,y) и ординатой точки касания MC, есть величина постоянная, равная 3.

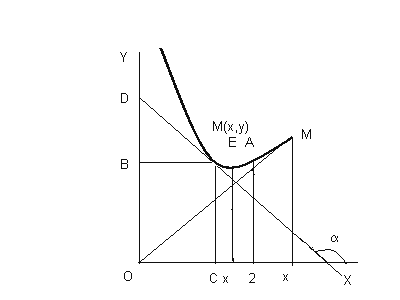Решение. Имеем

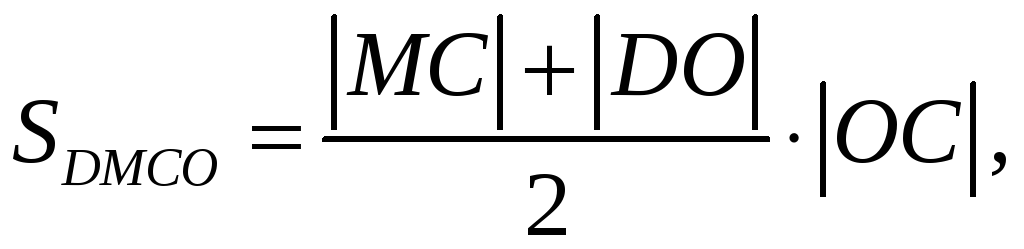
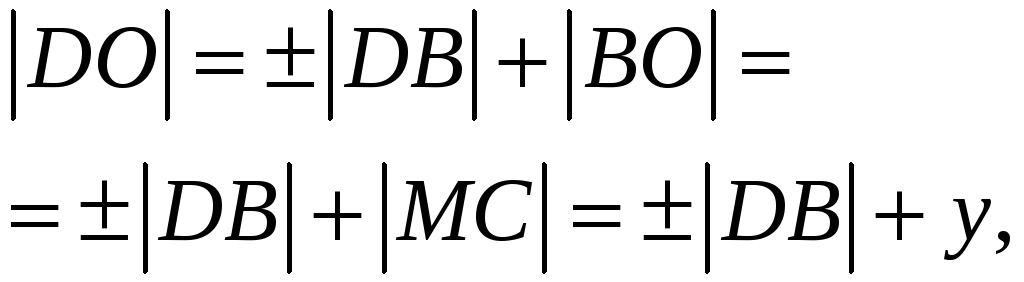
где перед ставится знак «+», если tg (левее точки минимума на рисунке), и знак «–», если tg. Поэтому в обоих случаях имеем: Далее находим:

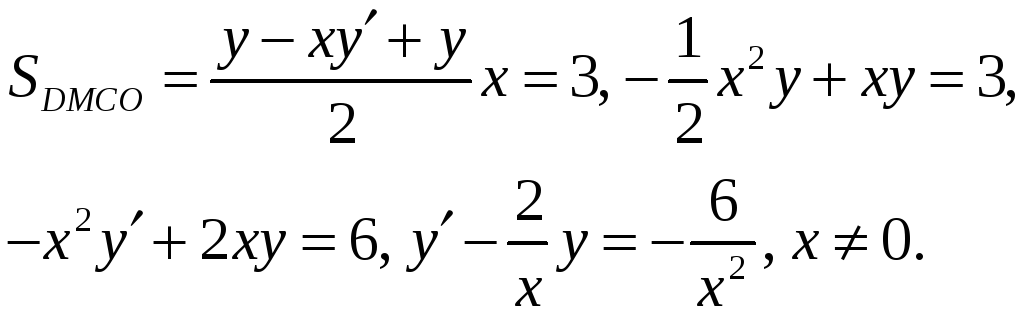
Получили линейное уравнение первого порядка. Решаем его:

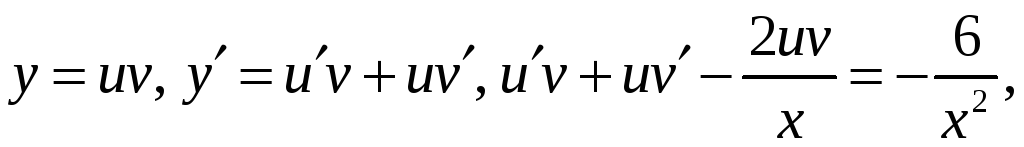
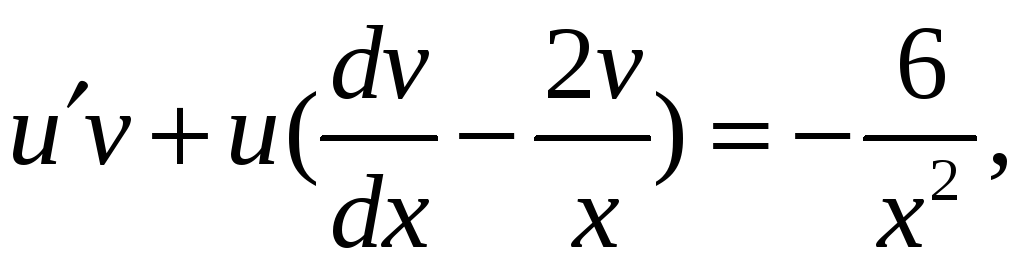(1)

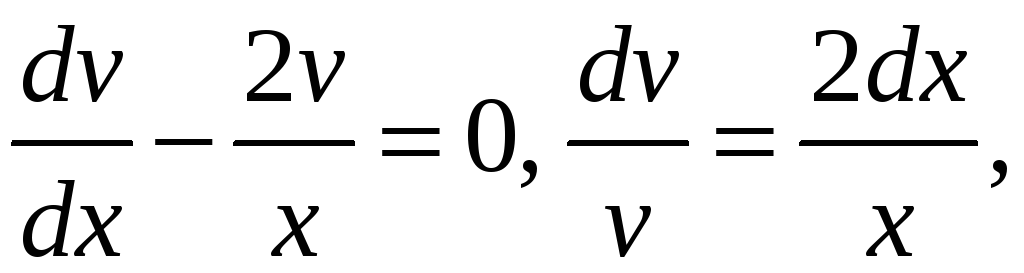
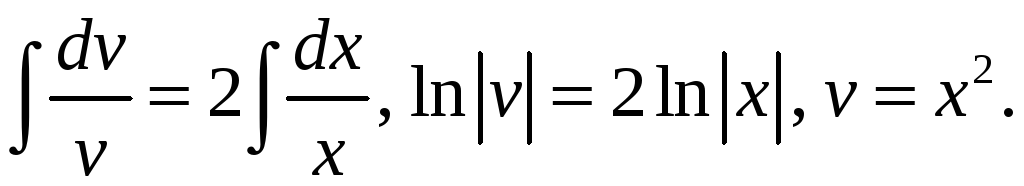
Подставим найденное выражение для в уравнение (1): . Отсюда находим :

.

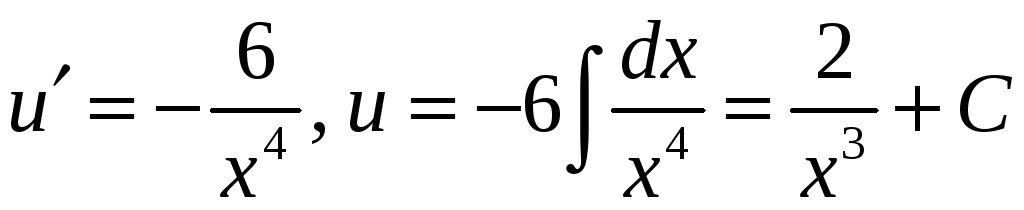Тогда .

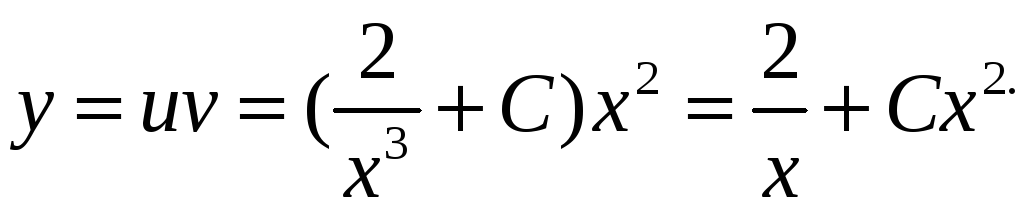Поскольку кривая проходит через точку , то, подставляя эти значения в общее решение, получим C=1/4. Искомая кривая имеет уравнение 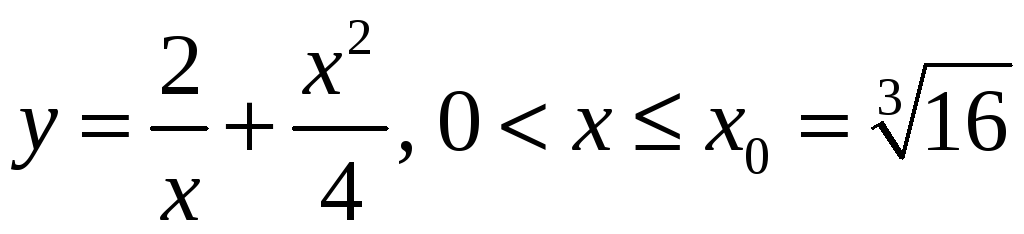. При имеем точку минимума.

Ответ: 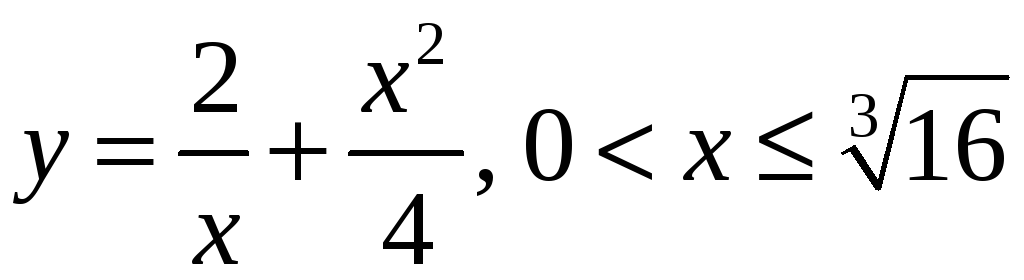– общее решение.

Список рекомендуемой литературы

1. Степанов В.В.Курс дифференциальных уравнений / В.В.Степанов. М.: ГИТТЛ, 1953.

2. Тихонов А.Н. Дифференциальные уравнения / А.Н. Тихонов, А.Б.Васильева , А.Г. Свешников. М.: Наука, 1980.

3. Демидович Б.П. Краткий курс высшей математики / Б.П.Демидович, В.А. Кудрявцев – М.: ООО «Издательство АСТ», 2003.

4. Дифференциальные уравнения: Методические указания по курсу «Высшая математика» / А.В.Зенков, В.Б. Соловьянов, О.Ю. Муйземнек. Екатеринбург: УГТУ, 1997.

5. Дифференциальные уравнения: Индивидуальное домашнее задание / Н.В.Быкова [и др.]. Свердловск: Изд. УПИ, 1991.

25