лекції по економетрії

статистик має показувати, які з пояснюючих змінних в більшій мірі підвержені мультиколінеарності.

Крок 3. з‘ясовується, яка пояснююча змінна породжує мультиколінеарності, та вирішується питання про її виключення з аналізу. Для цієї цілі розраховується коефіцієнт частинної кореляції rjk12…m (j, k=1,2,…,m; j<>k) між пояснюючими змінними. Змінна y в розрахунок не береться. В якості критерію використовується величина

що має t-розподіл з f=n-m ступенями вільності. Якщо tj,k>tα,f , то між змінними існує колінеарність и одна з них має бути виключеною. При

виключенні змінної дослідник має опиратися як на власну інтуїцію, та ы на змістовну теорію явища. Якщо tj,k ≤ tα,f , то дані не підверджені наявності мультиколінеарності між змінними xо та xл .

Лекція 5 Особливі випадки у багатофакторному регресійному аналізі:

гетероскедастичність

1.Поняття гетероскедастичності

2.Методи визначення гетероскедастичності

3.Вилучення гетерокседастичності

4.Узагальнений метод найменших квадратів (метод Ейткена)

Одним з основних припущень моделі класичної лінійної регресії є припущення про сталість дисперсії кожної випадкової величини е. (гомоскедастичність).

Формалізовано це припущення записується у вигляді:

Якщо це припущення не задовольняється у якомусь окремому випадку, то

має місце гетероскедастичність: Звичайно, нас буде цікавити питання про доцільність цього припущення і про

те, що відбувається, коли припущення про сталість дисперсії випадкової величини є не задовольняється. Отже, спробуємо розглянути:

1)природу, або суть гетероскедастичності;

2)наслідки гетероскедастичності;

3)можливості тестування гетероскедастичності;

4)які корективні заходи потрібно вжити в разі порушення гетероскедастичності?

1. Поняття гетероскедастичності

Суть припущення гомоскедастичності полягає в тому, що варіація кожної et

навколо її математичного сподівання не залежить від значення х. Дисперсія кожної ei. зберігається сталою незалежно від малих чи великих значень факторів: σ2e не є функцією xij тобто σ2e<> f(x1i, x2i,...,xpi ).

Графічно випадок гомоскедастичності для простої лінійної регресії показано випадковою дисперсією е у межах сталої відстані навколо лінії регресії (див. мал. 1 а).

Якщо σ2e не є сталою, а її значення залежать від значень х, можемо записати У цьому разі маємо справу з гетероскедастичністю. Графічна форма розкиду спостережень залежить від форми гетероскедастичності, тобто форми зв'язку між σ2e та хi На мал. 1 (б, в, г) показано три різні форми гетероскедастичності. Зокрема на мал. 1-6 показано випадок (монотонно) зростаючої дисперсії σ2e (із зростанням х зростає і дисперсія є).

Це загальноприйнята форма гетероскедастичності, що допускається в економетричних дослідженнях. На мал. 1-в показано випадок спадної гетероскедастичності: коли х набуває більших значень, відхилення спостережень від лінії регресії зменшується, таким чином дисперсія випадкової змінної зменшується із зростанням х. На мал. 5.3-г зображено більш складну форму гетероскедастичності: спочатку дисперсія є зменшується із зростанням де, але після певного рівня х* починає зростати із зростанням х. Зрозуміло, що форма гетероскедастичності залежить від знаків та значень коефіцієнтів у залежності Оскільки eі — неспостережувана випадкова величина, ми не знаємо справжньої форми

гетероскедастичності .

У прикладних дослідженнях, як правило, використовується зручне припущення, що гетероскедастичність (у разі простої лінійної регресії) має

форму σ2 = k2 x2 , де k — константа, яку потрібно оцінити.

ei i

Убагатьох економетричних дослідженнях може очікуватись, що припущення про сталу дисперсію випадкової змінної не зберігатиметься. Це можна легко зрозуміти, якщо врахувати фактори, вплив яких абсорбується значенням помилки. Згадаємо, що випадкова величина є виражає вплив на залежну змінну помилок в її вимірюванні та неврахованих факторів. У обох випадках є підстави для зміни з часом дисперсії е. Помилки вимірювання мають тенденцію до накопичення з плином часу, тому їхня величина збільшується.

Утакому разі дисперсія єі збільшується із зростанням значень х. З іншого боку, техніка вибірки та інші методи збору даних постійно вдосконалюються

і тому похибки вимірювання можуть зменшуватися. У такому разі σ 2 також

ei

зменшуватметься. Але важливіше те, що багато із неврахованих змінних можуть змінюватись в однаковому з х напрямку, викликаючи, таким чином, збільшення відхилення спостережень від лінії регресії.

Розглянемо вибірку фірм певної галузі з метою оцінки виробничої функції Кобба — Дугласа. У цьому разі g вміщує в собі такі фактори, як підприємництво, технологічні відмінності заводів різних фірм, відмінності у навиках чи організації та інші фактори. Ці фактори не мають значного коливання у малих фірмах і значно варіюють у великих фірмах. Отже, є будуть гетероскедастичними. Підсумовуючи, зазначимо, що апріорі є підстави стверджувати: на практиці припущення про гомоскедастичність порушуються. Тому важливо дослідити наслідки гетероскедастичності при оцінці невідомих параметрів та їхніх середньоквадратичних відхилень. Доведено, що звичайний випадок гетероскедастичності — це зростаюча дисперсія є1.

Наслідками порушення умови гомоскедастичність є: неможливість перевірки значимості параметрів регресії та побудови інтервалів довіри (дисперсія випадкової величини не стала, а змінюється), якщо вони отримані за методом найменших квадратів, і таким чином, оцінки параметрів регресії втрачають таку перевагу над іншими оцінками, як те, що вони мали найменшу дисперсію.

Тому оцінки параметрів доцільно знаходити за узагальненим методом найменших квадратів (інша назва – метод Ейткена)

2. Методи визначення гетероскедастичності

Отож перед нами постає важливе питання: як у конкретній ситуації можна довідатись про гетероскедастичність?

Як і у випадку мультиколінеарності, єдиних правил її виявлення немає, а е різноманітні тести. Розглянемо найпростіші з них за змістом та за розрахунками.

1. Аналіз змісту проблеми

3. Тест рангової кореляції Спірмена Це найпростіший тест, який можна використовувати як до малих, так і до великих вибірок.

Спочатку запишемо коефіцієнт рангової кореляції Спірмана:

де d. — різниця між рангами, що приписуються двом характеристикам і-го об'єкта;

n — кількість об'єктів, що ранжуються.

Наведений коефіцієнт рангової кореляції може використовуватись для визначення гетероскедастичності таким чином.

Припустимо, yi=β0 +β1xi+εi.

Етап 1. Побудувати регресію для даних у та х і розрахувати відхилення еi . Етап 2. Нехтуючи знаком еi , тобто беручи абсолютні значення | еi |, ранжуємо |ei | та хi у зростаючому чи спадному порядку і підрахуємо коефіцієнт рангової кореляції Спірмана.

Етап 3. Перевіряємо значимість отриманого коефіцієнта рангової кореляції за f-критерієм Ст'юдента. Для цього побудуємо t-статистику:

де n — кількість спостережень та df = (n - 2) — кількість ступенів вільності. При даних ступенях вільності за таблицями Ст'юдента знаходимо t . Якщо розраховане значення перевищує tкр (t > tкр ), це підтверджує гіпотезу про гетероскедастичкість. Якщо t ≤ tкр , тоді в регресійній моделі правильним є припущення про гомоскедастичність.

4. Тест Глейзера

Розглянемо його алгоритм на прикладі простої лінійної регресії.

Етап 1. Знаходимо невідомі параметри простої лінійної регресії методом найменших квадратів та обчислюємо помилки eі для кожного окремого спостереження.

Етап 2. Будуємо регресію, яка пов'язує абсолютні значення знайдених на першому етапі помилок (|еі |) з незалежною змінною х. Ми беремо абсолютні значення помилок, а не їхні справжні значення, бо Σех=0 , і том не можливо буде підібрати регресію е = f(x). Фактична форма цієї регресії звичайно не відома, тому до неї можна підбирати різні форми кривих. Глейзер пропонував такі залежності:

Обираємо ту регресію, яка найкраще підходить з огляду на коефіцієнт кореляції та середні квадратичні відхилення параметрів b0 та b1. (Зверніть увагу, що коли b0= 0 та b1<> 0, така ситуація називається "чиста гетероскедастичність"; якщо b0 та b1><0, цей випадок називається "змішана гетероскедастичність"). Гетероскедастичність визначається в світлі статистичної значимості параметрів b0 та b1, тобто ми виконуємо будь-який стандартний тест перевірки на значимість параметрів, і якщо вони значно відрізняються від нуля, то є, є гетероскедастичними. Перевага тесту Глейзера в тому, що він дає також інформацію про форму гетероскедастичності, тобто про спосіб, яким пов'язані еі та х. Ця інформація є важливою, як ми зараз побачимо, для "корекції" гетероскедастичності. Зазначимо, що у разі багатофакторної регресії на етапі 1 знаходимо помилки еі для регресії, що вміщує всі фактори. На етапі 2 будуємо залежності між абсолютними величинами знайдених помилок та залежною змінною у.

Слід зазначити, що деякі статистики надають перевагу тестам рангової кореляції Спірмана і Голдфелда та Квондта перед тестом Глейзера для визначення гетероскедастичності. Якщо якимось із цих тестів виявлено Гетероскедастичність, тоді можна експериментувати з функцією Глейзера з метою вирішення, які зміни початкових даних необхідні, щоб подолати uетероскедастичність.

5. Тест Голдфелда та Квондта

Цей тест застосовується до великих вибірок. Спостережень має бути хоча б удвічі більше, ніж оцінюваних параметрів. Тест припускає нормальний розподіл та незалежність випадкової величини εі.

Для застосування тесту сформулюємо нульову та альтернативну гіпотези. Нульова гіпотеза Н0 : εі гомоскедастична проти альтернативної гіпотези Н1: εі гетероскедастична (із зростаючою дисперсією).

3. Вилучення гетероскедастичності

Коли на базі будь-якого тесту встановлено гетероскедастичність, то для її вилучення змінюють початкову модель таким чином, щоб помилки мали постійну дисперсію. Далі невідомі параметри трансформованої моделі розраховуються за методом найменших квадратів. Трансформація моделі зводиться до зміни первісної форми моделі. Яким чином це проводиться, залежить від специфічної форми гетероскедастичності, тобто від форми

залежності між дисперсією σ 2 та значеннями незалежних змінних:

ei

σ2 =f(xi)

ei

Розглянемо можливі випадки трансформації моделі на прикладі простої лінійної регресії. Припустимо, що ми маємо початкову модель yi = β0 + β1xi + εi ( де випадкова величина εi гетероскедастична, але відповідає всім іншим класичним припущенням лінійної регресії.

Випадок 1. Припустимо, гетероскедастичність має форму E(ei )2 = σ 2 = k2 x2

ei

(де k — скінчена константа), тобто дисперсія є зростає пропорційно до х2 .

Виражаючи коефіцієнт пропорційності k 2, маємо k2 = σ 2 /х2 Це означає, що

ei

трансформація моделі полягає у діленні початкової моделі на x2 = x .Трансформована таким чином модель має вигляд:

Зверніть увагу на місце параметрів моделі: параметр при змінній 1/хi у трансформованій моделі є перетином у початковій моделі, тоді як перетин трансформованої моделі є нахилом початкової.

Нове змінене значення випадкової величини εі/хі є гомоскедастичним.

Отже, нова випадкова змінна має скінчену постійну дисперсію (що дорівнює k2 ), і, таким чином, ми можемо застосувати класичний метод найменших квадратів до розрахунку невідомих параметрів трансформованої моделі.

Випадок 2. Припустимо, що гетероскедастичність має форму

E(εi)2=σ 2 =k2xi

ei

Допустима трансформація полягає в діленні початкової моделі на (х)^1/2 , тобто трансформована модель має вигляд:

Для трансформованої моделі випадкова величина ε / x гомоскедастична із сталою дисперсією k2 .

Випадок 3. Припустимо, що форма гетероскедастичності

E(εi)2=σ 2 =k2 (a0+a1 xi )2

ei

Допустима трансформація полягає в діленні початкової моделі на

(a0 + a1 x)2 = (a0 + a1 x), тобто

Нова випадкова величина є гомоскедастичною із сталою дисперсією, рівною k2 . Справді, маємо:

Загальний випадок Коли гетероскедастичність має вираз

де — скінчена константа і f(xi ) — функція від х, трансформація початкової початкової моделі здійснюється шляхом її ділення на f (xi ) . Пояснимо, чому

саме така трансформація необхідна. Взагалі, наведена вище трансформація еквівалентна застосуванню методу зважених найменших квадратів (ЗНК), який є особливим випадком методу узагальнених найменших квадратів (УНК). Опишемо метод зважених найменших квадратів (ЗНК), який забезпечує обґрунтування вищенаведеної трансформації.

Уметоді простих найменших квадратів ми мінімізуємо просту суму квадратів відхилень:

åei2 = å(y − b0 − b1 xi )2

Уякій кожне відхилення має однакову вагу (сума ваг =1). Тобто сума Σ ei2 є

незваженою сумою квадратних відхилень, у якій припускається, що εі , оцінені за допомогою еі . Хоча, якщо дисперсія єі не є сталою, а, скажімо, зростає із збільшенням де, зрозуміло, що більша дисперсія спостереження дає менш точну вказівку на те, де проходить правильна регресійна лінія. Тому здається правдоподібним надавати меншої уваги цим спостереженням у підборі лінії регресії порівняно з іншими спостереженнями. Цього можна досягнути наданням різної ваги кожній єі (чи її оцінці). Інколи доцільно

використовувати як вагу частку 1 /σ 2 , тобто поділити кожне відхилення на

ei

дисперсію випадкової величини. У випадку, коли випадкова величина eі є

чином, великим помилкам надаються малі ваги. Отже, замість мінімізації простої суми квадратів відхилень ми мінімізуємо зважену суму квадратів відхилень:

Такий метод і називається методом зважених найменших квадратів (ЗНК). Прирівнявши часткові похідні зваженої суми квадратів до нуля і розв'язавши систему рівнянь, отримаємо формули для знаходження невідомих параметрів

b0 та b1, що можливо при відомій дисперсії σ 2 . . Але на практиці ця

ei

дисперсія, як правило, невідома, і процедура її обчислення може бути досить складною. Що ж робити, коли дисперсія невідома? В такому випадку наведені вище трансформації початкової моделі аналогічні застосуванню методу зважених найменших квадратів для початкової моделі.

Можна довести, що мінімізація зваженої суми квадратів відхилень виводить аналогічні формули для оцінок невідомих параметрів початкової моделі, як і застосування простого методу найменших квадратів до трансформованої моделі.

Ефективність оцінок трансформованої моделі

Як було показано вище, тест, запропонований Глейзером, дає інформацію

про форму гетероскедастичності. Експериментуючи з різними формами функції | е| = f(x), ми можемо обрати найкращу, а потім перейти до трансформації початкової моделі, як описано раніше.

Доведено, що оцінки трансформованої моделі мають меншу дисперсію (є ефективнішими), ніж оцінки, отримані із застосуванням методу найменших квадратів до початкової моделі.

Слід звернути увагу, що гетероскедастичність може траплятися через невраховані змінні, тобто через погану специфікацію моделі. У цьому випадку можливим рішенням є включення неврахованих змінних у модель. Сліпе застосування трансформації, наведеної вище, зробить гомоскедастичною випадкову змінну, але оцінки параметрів можуть залишатися неправильними через неврахування важливих факторів. З економічної теорії відомо, що, наприклад, у функції заощаджень гетероскедастичність може виникати через зміни в економічній політиці (монетарна політика, податкові реформи, знецінення національної валюти). У цьому разі рішенням буде врахування у функції певних факторів, які б відбивали зміни в політиці уряду.

4. Узагальнений метод найменших квадратів (метод Ейткена)

На відміну від звичайного методу найменших квадратів (МНК), узагальнений метод (УНК) враховує інформацію про неоднаковість дисперсії і тому здатний створити BLUE-оцінки, тобто оцінки, що мають найменшу дисперсію.

Ідея УНК полягає в наступному.

Щоб проілюструвати це, знову повернемося до простої лінійної регресії:

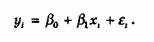(1)

Простою математичною маніпуляцією перепишемо () у вигляді:

(2)

де x0t = 1 для кожного і.

Припустимо, що наявна гетероскедастичність і всі дисперсії σ i2 відомі. Поділимо (2) на σi, отримаємо:

(3)

Для зручності перепишемо (3) у вигляді:

(4)

де зірочками помічені початкові змінні, поділені на відомі σi. Позначення β0* та β1* використовуються для того, щоб відрізнити їх від звичайних параметрів β0 та β1, отриманих методом найменших квадратів.

У чому полягає мета трансформації першої моделі? Тепер дисперсія трансформованої помилки є* є постійною величиною, тобто для моделі (4)

зберігається припущення про гомоскедастичність, і ми переходимо до класичної регресійної моделі. Справді,

(5)

Ми припускали, що σi — відомі, звідси маємо:

Як же отримати оцінки для β0* та β1* ? Для моделі (5) запишемо вибірковий аналог:

Для того, щоб знайти невідомі параметри за методом узагальнених найменших квадратів, мінімізуємо:

ån ei*2 = ån (yi* - b0* x0*i - b1* xi* )2 (7) i=1 i=1

або

(8)

Розрахунки наводити не будемо і запишемо лише кінцевий результат. УНКоцінка для β1* дорівнює:

Різниця між звичайним та узагальненим методом найменших квадратів За методом звичайних найменших квадратів невідомі параметри знаходяться

шляхом мінімізації суми квадратів відхилень фактичних значень від теоретичних. Для простої лінійної регресії маємо:

В узагальненому методі найменших квадратів мінімізується вираз (8), який можна переписати у вигляді:

(11)