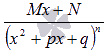Коллоквиум
.docxБилет
№1



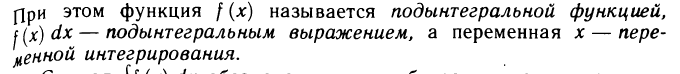
Билет №2
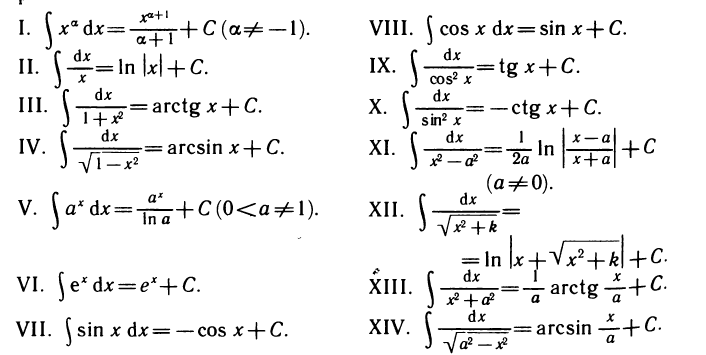
Билет №3


Билет №4

Билет №5
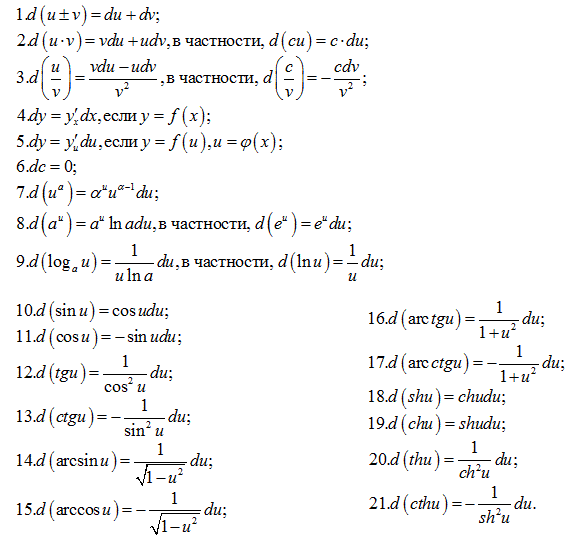
Билет №6
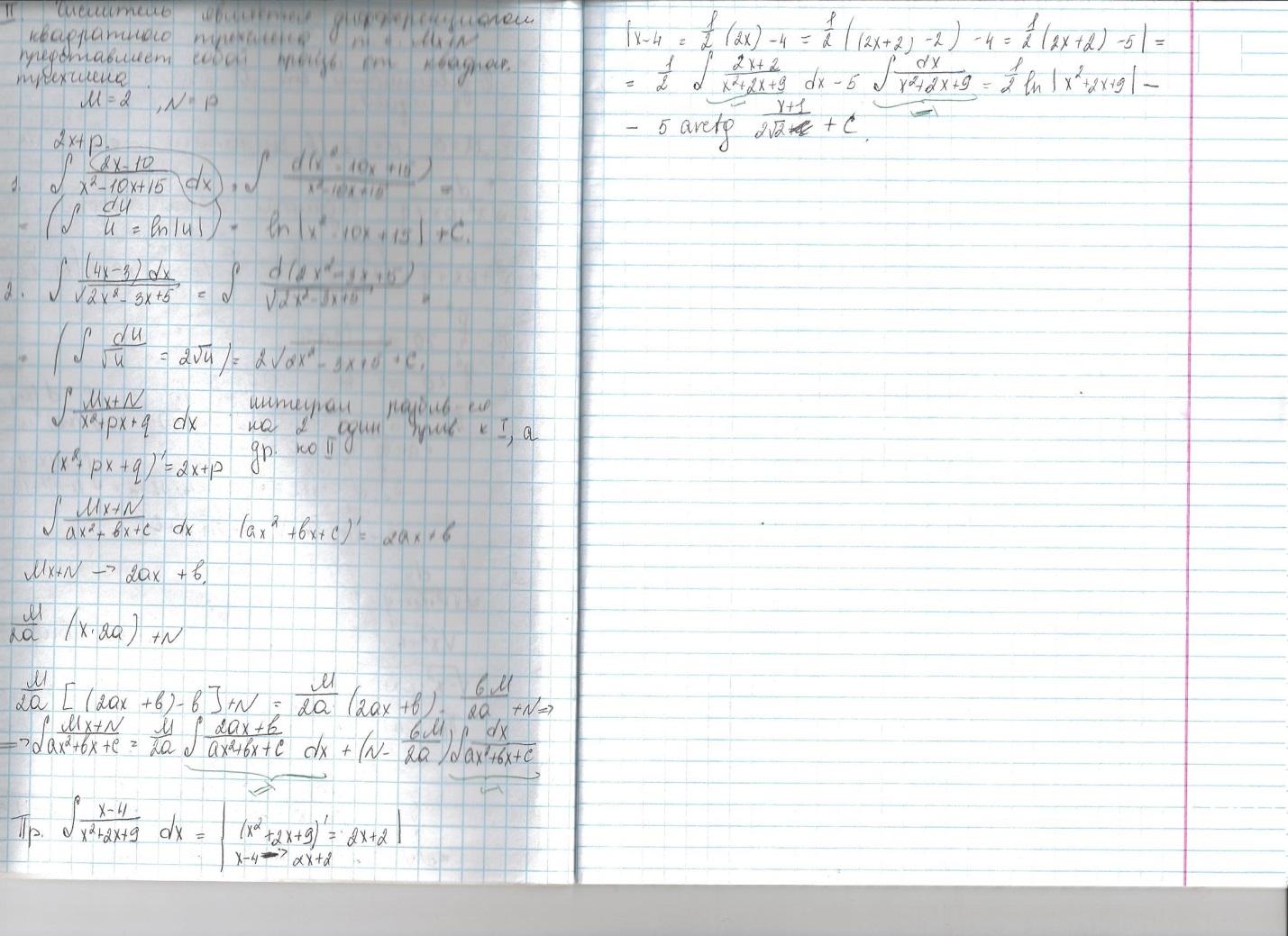
Билет
№7

Билет
№8 Билет
№9
Всякий многочлен с
любыми комплексными коэффициентами ,
степень которого не
Билет
№9
Всякий многочлен с
любыми комплексными коэффициентами ,
степень которого не
меньше единицы имеет хотя бы один корень, в общем случае комплексный.
Билет №10 Различают следующие виды простейших дробей:
Билет №11


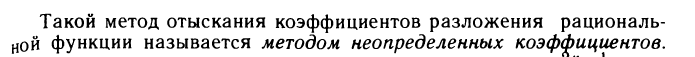
 Билет
№12
Билет
№12
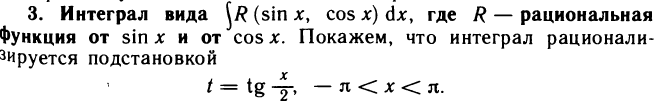
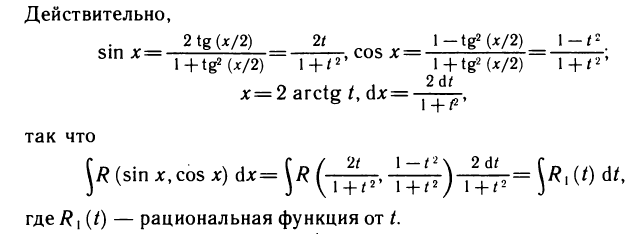
Билет №13
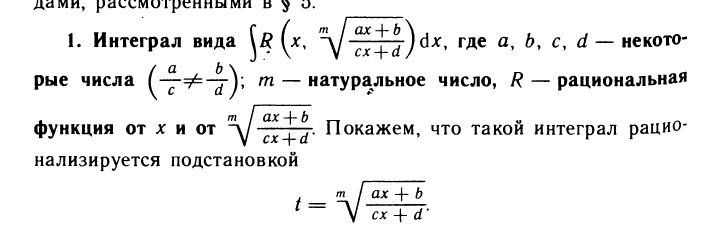
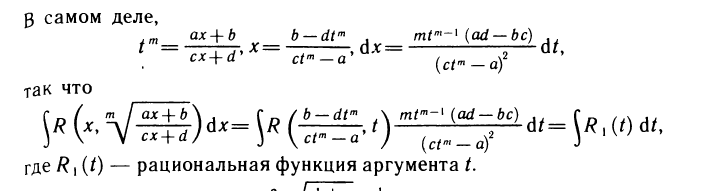

 Билет
№14
При
вычислении производной, наличие формул
для производной суммы, разности,
произведения, частного и композиции --
всех тех операций, при помощи которых
элементарные функции образуются из
минимального набора -- приводит к
тому, что производная любой элементарной
функции снова является элементарной
функцией. При нахождении неопределённых
интегралов, однако, формул для первообразной
произведения, частного и композиции
нет. Это приводит к такому положению,
что отнюдь не для любой элементарной
подынтегральной функции можно "взять
интеграл", то есть выразить некоторую
первообразную для подынтегральной
функции в виде некоторого выражения,
использующего лишь элементарные функции.
Дело не в том, что пока что не придумано
способа это сделать, а в принципиальной
невозможности: никакая из первообразных
в случае "неберущегося" интеграла
никаким образом не может быть выражена
как комбинация элементарных функций,
связанных знаками арифметических
действий и знаками композиции. Не следует
думать, что если такое представление
невозможно, то и функции такой нет1:
можно считать, что для её выражения
просто не хватает запаса рассматриваемых
операций или запаса рассматриваемых
исходных функций, и их надо расширить,
то есть выйти за рамки множества функций,
называемых элементарными2.
В науке и её приложениях в технике,
экономике и других дисциплинах применяются
многие неэлементарные функции; часто
их называют специальными.
К специальным функциям относятся и
многие первообразные для элементарных
функций, причём часто не столь уж
"сложной" структуры. Интегралы,
выражающиеся через такие первообразные,
называются (по традиции, берущей начало
в 18 веке) неберущимися.
Итак, интеграл
Билет
№14
При
вычислении производной, наличие формул
для производной суммы, разности,
произведения, частного и композиции --
всех тех операций, при помощи которых
элементарные функции образуются из
минимального набора -- приводит к
тому, что производная любой элементарной
функции снова является элементарной
функцией. При нахождении неопределённых
интегралов, однако, формул для первообразной
произведения, частного и композиции
нет. Это приводит к такому положению,
что отнюдь не для любой элементарной
подынтегральной функции можно "взять
интеграл", то есть выразить некоторую
первообразную для подынтегральной
функции в виде некоторого выражения,
использующего лишь элементарные функции.
Дело не в том, что пока что не придумано
способа это сделать, а в принципиальной
невозможности: никакая из первообразных
в случае "неберущегося" интеграла
никаким образом не может быть выражена
как комбинация элементарных функций,
связанных знаками арифметических
действий и знаками композиции. Не следует
думать, что если такое представление
невозможно, то и функции такой нет1:
можно считать, что для её выражения
просто не хватает запаса рассматриваемых
операций или запаса рассматриваемых
исходных функций, и их надо расширить,
то есть выйти за рамки множества функций,
называемых элементарными2.
В науке и её приложениях в технике,
экономике и других дисциплинах применяются
многие неэлементарные функции; часто
их называют специальными.
К специальным функциям относятся и
многие первообразные для элементарных
функций, причём часто не столь уж
"сложной" структуры. Интегралы,
выражающиеся через такие первообразные,
называются (по традиции, берущей начало
в 18 веке) неберущимися.
Итак, интеграл ![]() не
берётся,
если функция
не
берётся,
если функция ![]() не
является элементарной. Приведём примеры
неберущихся интегралов и названия
первообразных -- специальных функций,
связанных с этими интегралами.
не
является элементарной. Приведём примеры
неберущихся интегралов и названия
первообразных -- специальных функций,
связанных с этими интегралами.
Пример 1.8 Неберущимся является интеграл
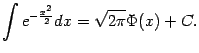
Здесь
одна из первообразных, которую мы
обозначили ![]() ,
выделяется из всего набора первообразных
условием
,
выделяется из всего набора первообразных
условием ![]() .
Функция
.
Функция ![]() называется функцией
Лапласа.
Она широко применяется в теории
вероятностей, физике, математической
и прикладной статистике и других разделах
науки и её приложений. Для вычисления
значений функции Лапласа составлены
таблицы, имеющиеся во многих учебниках,
задачниках и справочниках по теории
вероятностей и статистике. Возможность
вычисления предусмотрена также на
многих моделях калькуляторов (не самых
дешёвых) и уж, обязательно, на тех, что
предназначены для статистической
обработки числового материала. Так что,
с практической точки зрения, пользоваться
функцией Лапласа ничуть не сложнее,
чем, скажем, синусом, арктангенсом или
натуральным логарифмом, которые мы
условно относим к элементарным функциям.
называется функцией
Лапласа.
Она широко применяется в теории
вероятностей, физике, математической
и прикладной статистике и других разделах
науки и её приложений. Для вычисления
значений функции Лапласа составлены
таблицы, имеющиеся во многих учебниках,
задачниках и справочниках по теории
вероятностей и статистике. Возможность
вычисления предусмотрена также на
многих моделях калькуляторов (не самых
дешёвых) и уж, обязательно, на тех, что
предназначены для статистической
обработки числового материала. Так что,
с практической точки зрения, пользоваться
функцией Лапласа ничуть не сложнее,
чем, скажем, синусом, арктангенсом или
натуральным логарифмом, которые мы
условно относим к элементарным функциям.
Пример 1.9 Не берётся также интеграл
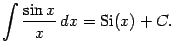
Доопределим
подынтегральную функцию ![]() ,
полагая её равной 1 при
,
полагая её равной 1 при ![]() .
В соответствии с тем, что
.
В соответствии с тем, что ![]() ,
доопределённая функция будет непрерывна
на всей числовой оси. Среди её
первообразных
,
доопределённая функция будет непрерывна
на всей числовой оси. Среди её
первообразных ![]() выделим
ту, для которой
выделим
ту, для которой ![]() .
Эта неэлементарная функция
называется интегральным
синусом и
обозначается
.
Эта неэлементарная функция
называется интегральным
синусом и
обозначается ![]() .
Именно её мы использовали в приведённой
выше формуле.
.
Именно её мы использовали в приведённой
выше формуле.
Пример 1.10 Ещё один неберущийся интеграл:

Одна
из первообразных -- та, что мы
использовали в правой части и
обозначили ![]() --
называется интегральным
косинусом.
--
называется интегральным
косинусом.
Пример 1.11
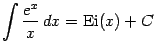 --
--
это
тоже неберущийся интеграл. Одна из
первообразных, которую мы обозначили ![]() , --
специальная функция, называющаяся интегральной
экспонентой.
, --
специальная функция, называющаяся интегральной
экспонентой.
Пример 1.12 Не берётся интеграл
 (при
(при ![]()
одна
из первообразных, ![]() ,
называется интегральным
логарифмом.
,
называется интегральным
логарифмом.
Билет
№15




 Билет
№16
Билет
№16


 Билет
№17
Билет
№17


 Билет
№18
Билет
№18
 Билет
№19
Билет
№19



 Билет
№20
Билет
№20

 Билет
№21
Билет
№21
Билет
№22
 Билет
№23
Билет
№23
 Билет
№24
Билет
№24
Билет
№25
 Билет
№26
Билет
№26


Билет №27

 Билет
№28
Билет
№28
Билет №29