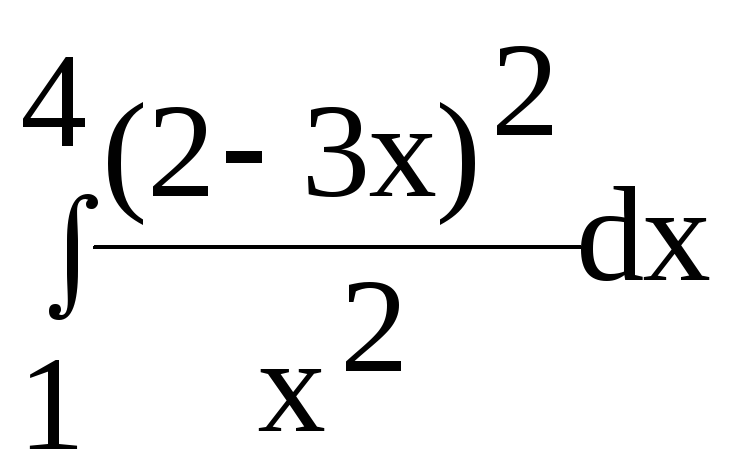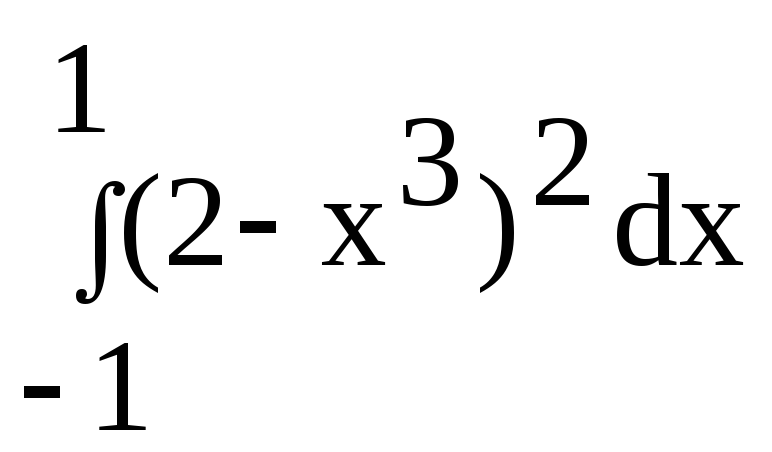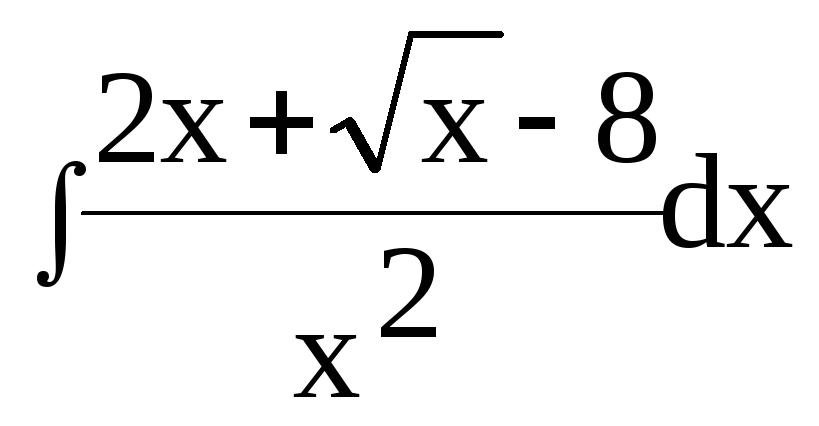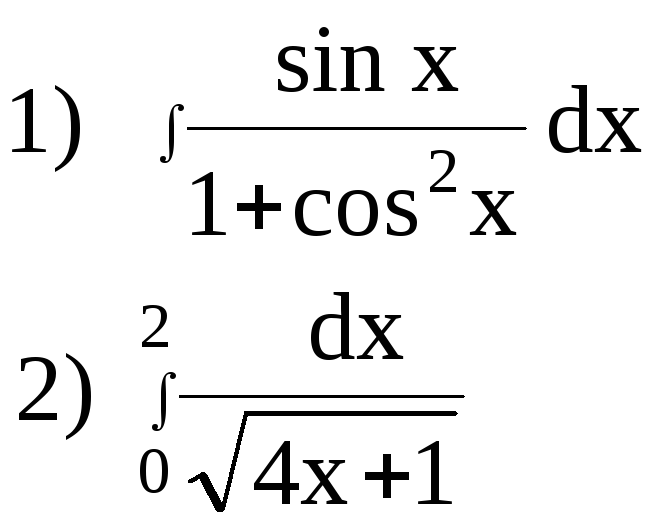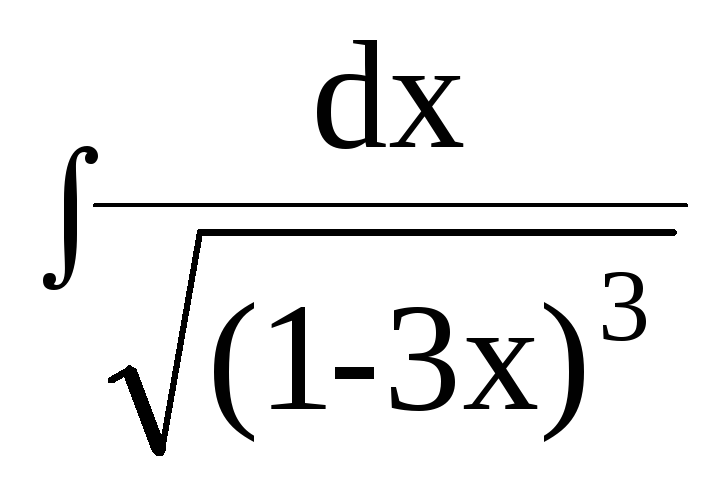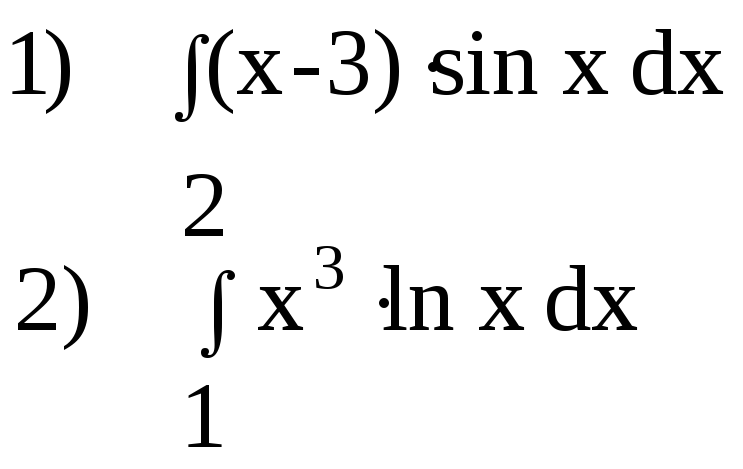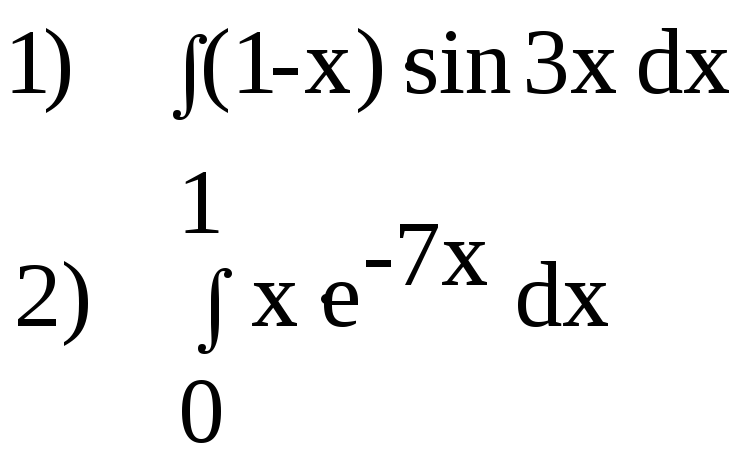Розділ І . Лінійна алгебра.

Приклад розв’язання типового завдання:

 1. Знайти матриці : а) С=А  В , б) Е=3 А-D , якщо

б)

Завдання 1.1

Задані матриці А, В, С; числа . Знайти матриці : 1) ; 2)

Варіанти завдань :

Варіант А

№	А	В	С
1				-2	3
2					-4
3				3	-1
4					4
5				2	1
6				-3	2
7				-1	3
8					5
9				4	-1
10				-5

Варіант Б

№	А	В	С
1				-3	2
2				5	-3
3					4
4					5
5				2	-1
6					-2
7				-2	3
8				-4	5
9				1
10				3	-1

Варіант В

№	А	В	С
1				-5
2				2	-1
3				-3	1
4					2
5					-2
6				4	-3
7					4
8				1	-2
9				5	3
10				4	2

 2. Розв‘язати систему рівнянь за методом Жорданових виключень.

Розв’язання. Нехай задана система лінійних рівнянь ,

Запишемо систему лінійних рівнянь у вигляді таблиці: Таблиця 1.

1. Вибираємо розв’язуючий елемент (будь-який не рівний 0). х1 х2 х3

Наприклад, “1”. Це означає, що перший рядок і третій 1 3 -2 1

стовпець - розв’язуючі. 5 4 1 0

-4 1 -5 4

2. Заповнюємо лівий стовпець і верхній рядок таблиці , враховуючи зміну місцями вільного члена 1 і невідомої х3.

Таблиця 2.

х1 х2 1 3. У новій таблиці замість розв’язуючого елемента пишемо

х3 -3 2 1 “1” поділена на розв’язуючий елемент, тобто ( 1/1=1).

5 4 1 0 4. Всі інші елементи розв’язуючого стовпця (третього) без змін

-4 -11 3 4 знака діляться на розв’язуючий елемент “1” і записуються у

третій стовпець нової таблиці (табл.2).

5. Елементи розв’язуючого рядка (першого) змінюють знак на протилежний, діляться на розв’язуючий елемент і записуються у перший рядок нової таблиці (табл.2).

6. Користуючись правилом “прямокутника” , обчислюємо всі інші елементи нової таблиці (табл.2).

В новій таблиці обираємо розв’язуючий елемент, наприклад “1”, якій стоїть у другому рядку і другому стовпці. У цьому випадку розв’язучий рядок другий і

розв’язуючий стовпець - другий. Заповнюємо нову таблицю за описаною схемою :

Таблиця 3.

х1 5 1

х3 -11 2 1

В отриманій таблиці 3 залишається поміняти х2 -4 1 0

місцями тільки невідому х1 і вільний член -4 -4 -23 3 4

Таблиця 4.

-4 5 1

х3 11/23 13/23 -21/23

х2 4/23 11/23 -16/23

х1 -1/23 3/23 4/23 З останньої таблиці знаходимо невідомі :

Перевірка : підкладаємо значення змінних у кожне рівняння системи

Відповідь : Х1=1 , Х2=1 , Х3=0 .

 Завдання 1.2. Розв’язати систему рівнянь за методом Жорданових виключень

Варіанти завдань :

Варіант А

1) 2) 3)

4) 5) 6)

7) 8) 9)

10)

Варіант Б

1)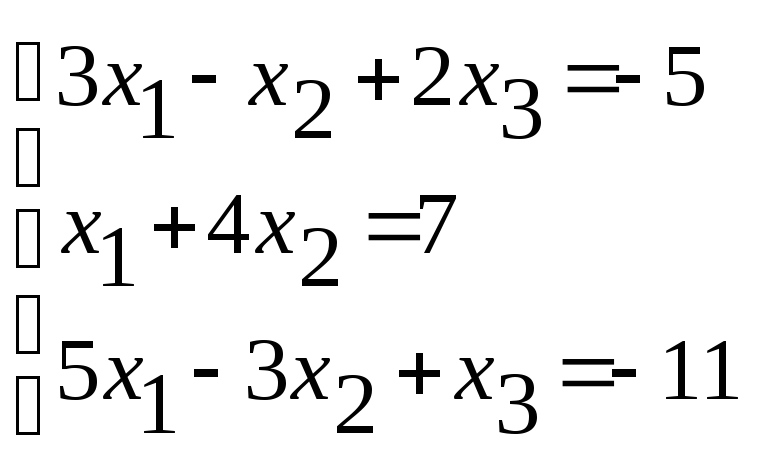 2) 3)

4) 5) 6)

7) 8) 9)

10)

Варіант В

1) 2) 3)

4) 5) 6)

7) 8) 9)

10)

 Розділ ІІ . Диференціальне числення.

Приклад розв’язання типового завдання:

 1. Дослідити функцію і побудувати її графік .

1. Область визначення функції D(х)=(-;+)

2. Функція парна : , тому її графік симетричний відносно осі OY.

3. Точки перетину графіка з віссю ОY : х=0 ; ; А (0 ; 3) .

з віссю ОХ: у=0 ; .

Робимо підстановку , тоді отримаємо

Отримаємо точки для побудови графіка : В(-4,1 ; 0) , С(-1,2 ; 0) , D(1,2 ; 0) , E(4,1 ; 0)

4. Для визначення точок екстремума знайдемо першу похідну функції :

x	(-;-3)	-3	(-3 ; 0)	0	(0 ; 3)	3	(3 ; +)
y’	-	0	+	0	-	0	+
y		min		max		min

Знайдені точки екстремуму : min(-3 ; -7,125) , min (3 ; -7,125) , max (0 , 3) .

5. Проміжки опуклості та вгнутості графіка визначаються за допомогою другої похідної

x	(- ; -3)	-3	(-3 ; 3 )	3	(3 ; +)
y”	+	0	-	0	+
y		перегин		перегин

Графік функції :

 Завдання 2.1. Дослідити функцію і побудувати її графік.

Варіанти завдань :

• А Б В

2. Знайти найменше та найбільше значення функції на

проміжку [-2 ; 4]

1. Знайдемо критичні точки заданої функції з умови

З розв’язаної задачі 1 критичні точки є:

2. Перевіряємо , чи належать критичні точки до заданого проміжку :

3. Обчислимо значення функції на кінцях заданого проміжку і в критичних точках, які належать до нього :

Відповідь : max y(x)=-1 ; min y(x)=-7,125.

[-2 ; 4] [-2 ; 4]

 Завдання 2.2. Знайти найменше та найбільше значення функції, заданої у попередньому завданні 2.1 на вказаному проміжку.

Варіанти завдань :

№ 1.	А [ 0 ; 3 ]	Б [ -1 ; 3 ]	В [ -3 ; 1 ]
2.	[ -1 ; 4 ]	[ 0 ; 3 ]	[ -1 ; 1 ]
3.	[ 0 ; 4 ]	[ 0 ; 3 ]	[ -1 ; 3 ]
4.	[ -1 ; 2 ]	[ -2,5 ; 0 ]	[ -4 ; 1 ]
5.	[ -0,5 ; 2 ]	[ -1 ; 2 ]	[ -0,5 ; 3 ]
6.	[ -2 ; 1 ]	[ -1 ; 2 ]	[ -1 ; 3 ]
7.	[ -1 ; 2 ]	[ -0,5 ; 2 ]	[ 1 ; 3 ]
8.	[ 0 ; 1 ]	[ -1 ; 3 ]	[ 1 ; 4 ]
9.	[ -1 ; 4 ]	[ -2 ; 1 ]	[ -3 ; 1 ]
10.	[ 0 ; 3 ]	[ -2 ; 1 ]	[ -1 ; 2 ]

3. Скласти рівняння дотичної і нормалі до графіка функції у точці Х0=2. Накреслити графік функції , нормалі та дотичної.

Рівняння дотичної має вигляд : .

Для нашого випадку :

Рівняння дотичної : (Т) .

Рівняння нормалі має вигляд : .

Для нашого випадку :

(N) .

Д ля побудови графіка функції знайдемо координати вершини параболи і точки перетину її з осями координат. Абсцису вершини параболи

обчислюємо за формулою : 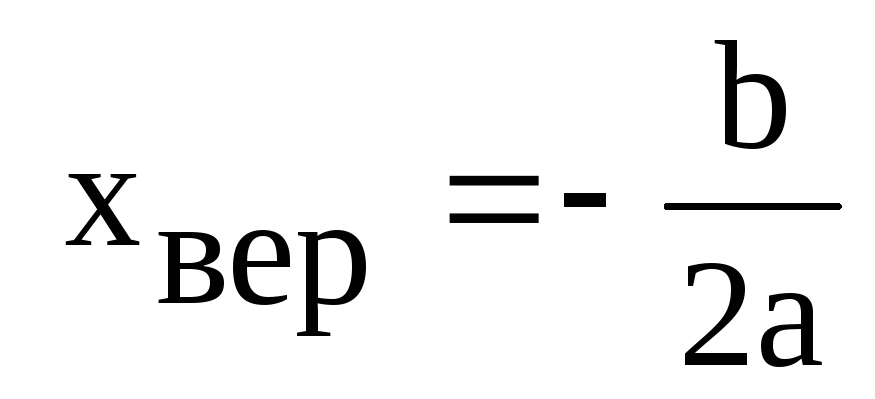. Для нашого випадку :

Точки перетину параболи з ОХ :

Отримаємо дві точки: (-0,75 ; 0) та (1,75 ; 0) .

 Завдання 2.3. Скласти рівняння дотичної і нормалі до заданої функції у(х) у заданій точці Х0 . Зробити малюнок.

Варіанти завдань : А Б В

4. Знайти похідні наступних функцій :

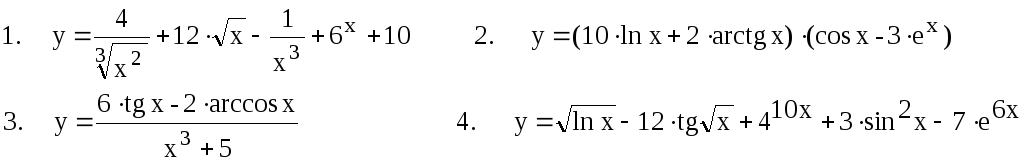
Р озв”язання :

 Завдання 2.4 Знайти похідні від заданих функцій.

Варіанти завдань :

А: Варіант

1

2

3

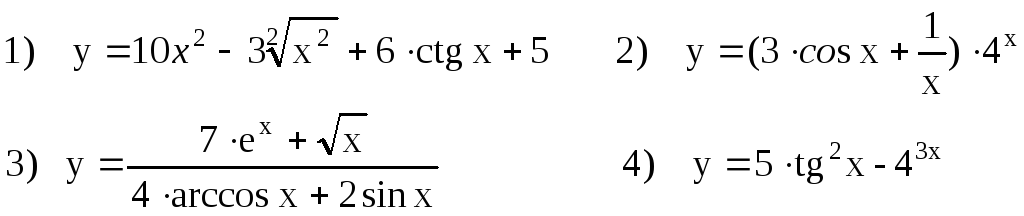
4

5

6

7

8

9

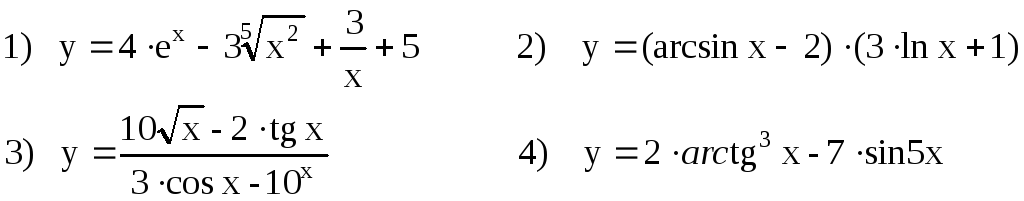
10

Б : Варіант

1.

B : Варіант

Розділ ІІІ . Границя функції.

Приклад розв’язання типового завдання:

 1. Знайти границі функцій:

 Зауваження :



Завдання 3.1. Знайти границі заданих функцій, якщо

1) а) Х0=0 , б) Х0=

Варіанти завдань :

А :

В аріант

Б :

В аріант

В :

В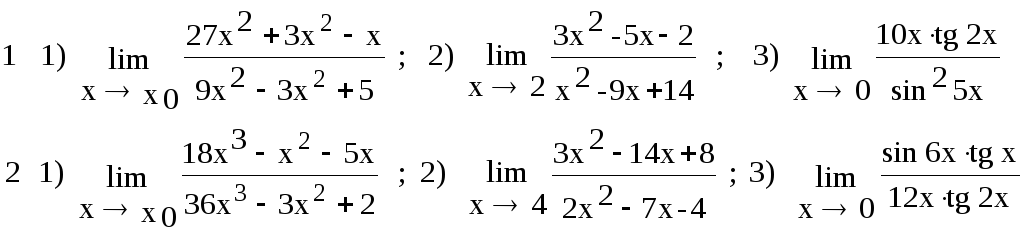 аріант

Розділ ІV . Інтегральне числення.

Приклад розв’язання типового завдання:

• 1. За допомогою основних методів інтегрування знайти інтеграли : Безпосереднє інтегрування

1)

 Завдання 4.1 1) Знайти невизначений інтеграл ;

2) Обчислити визначений інтеграл Варіанти завдань :

№	А	Б	В
1	1) 2)	1) 2)	1) 2)
2		1) 2)	1) 2)
3	1) 2)	1) 2)	1) 2)
4	1) 2)	1) 2)	1) 2)
5	1) 2)	1) 2)	1) 2)
6	1) 2)	1) 2)	1) 2)
7	1) 2)	1) 2)	1) 2)
8	1) 2)	1) 2)	1)
9	1) 2)	1) 2)	1) 2)
10	1) 2)	1) 2)	1) 2)

Інтегрування методом підстановки.

2. 

 Завдання 4.2 Обчислити інтеграли за методом підстановки.

Варіанти завдань :

№	А	Б	В
1	1) 2)	1) 2)	1) 2)
2	1) 2)
3	2)
4
5
6
7
8
9
10

Інтегрування частинами.

3. 

 Завдання 4.3 Розв’язати за методом інтегрування частинами

Варіанти завдань .

№	А	Б	В
1
2
3
4
5
6
7
8
9
10

• 2. Обчислити площу фігури, обмежену лініями :

Розв’язок : Знайдемо точки перетину заданих парабол. Для цього розв’яжемо систему рівнянь : .

Розв”яжемо одержане квадратне рівняння

Обчислимо відповідні значення функції

Маємо дві точки перетину : А(-1 ; 1) , В(4 ; -9) .

Побудуємо параболи в системі координат

 Завдання 4.4 Обчислити площу фігури, обмежену заданими параболами.

Варіанти завдань:

Варіант А Б В

 Розділ V . Аналітична геометрія на площині.

Приклад розв’язання типового завдання:

Для трикутника АВС задано координати вершин: ,.

Потрібно: 1) записати рівняння , знайти довжину :

а) сторони АВ;

б) медіани СД;

в) висоти СF;

2) знайти кут між прямими АВ і АС .

Нехай А(-3;-3), В(4;3), С(2;7). Покажемо  АВС в декартовій cистемі координат.

1. а) Рівняння АВ ;

6(x+3)=7(y+3) ;

Кутовий коефіцієнт прямої АВ

Довжина АВ :

б) Рівняння медіани СД : Д – середина АВ тому

Запишемо рівняння СД :

; ; -7(x-2)= -3/2(y-7) ;

Довжина СД :

в) Рівняння висоти СF :

За умовою перпендикулярності прямих АВ і CF:

Тому, кутовий коефіцієнт висоти СF:

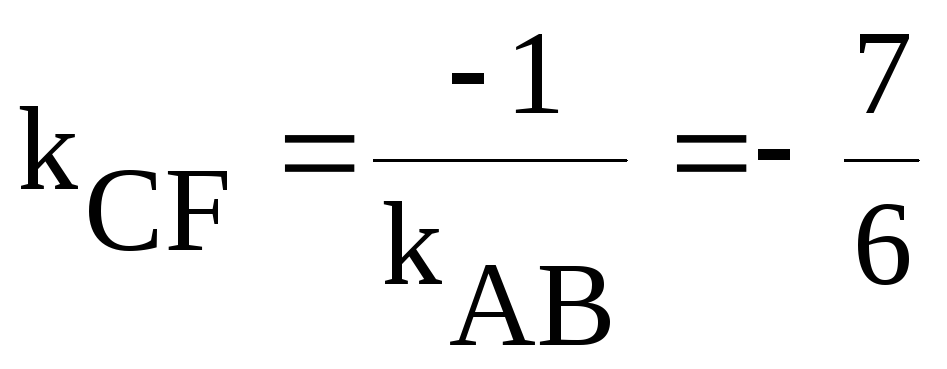
Рівняння СF :

Довжина СF :

Знайдемо точку перетину прямих АВ і СF. Для цього складаємо систему із рівнянь прямих АВ і СF і розв”язуємо її :

Підставляємо знайдене “х” у будь яке рівняння системи :

2) Кут між прямими АВ і АС :

Щоб знайти кут між прямими АВ і АС треба знати кутові коефіцієнти прямих. Кутовий коефіцієнт АВ : . Кутовий коефіцієнт прямої АС :

Тоді кут ВАС трикутника знаходимо за формулою :

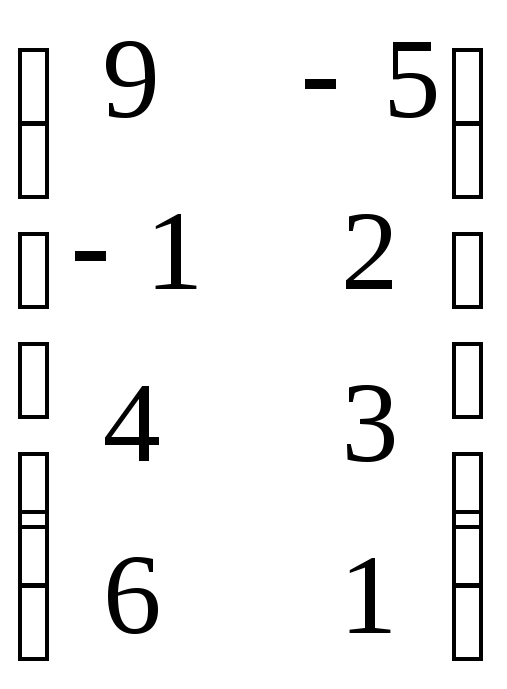
 Завдання 5.1. Задані координати вершин трикутника АВС . Необхідно :
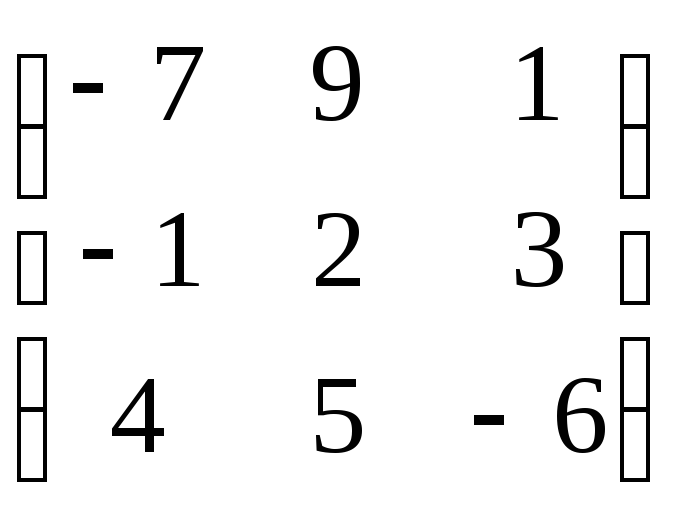