
Доронин Ю.П. Физика океана
.pdf
Библиотека сайта www.fluger.org
Океан в среднем обладает устойчивой плотностной стратификацией, т.е. более плотные слои воды располагаются под менее плотными. Чем больше вертикальный градиент плотности, тем труднее воду перемешать, так как на это требуется затратить больше энергии. При этом обычно затрудняется проникновение тепла, соли и других субстанций через слои с большой плотностной устойчивостью. Довольно часто под воздействием тех или иных причин происходит нарушение изложенной картины, и менее плотные массы воды оказываются под более плотными. Длительное время такая аномальная стратификация сохраняться не может, и в соответствии с законом Архимеда происходит опускание более плотной воды и подъем менее плотной. Характер этой циркуляции и связанный с ней перенос различных субстанций также зависят от вертикального градиента плотности. Поэтому в океанологической практике почти всегда оценивается плотностная устойчивость океанов и морей в том или ином пункте.
Критерий устойчивости определяется по соотношению плотностей перемещающегося по вертикали объема жидкости ρν и окружающей среды ρ. Считается, что плотность перемещающегося объема воды меняется адиабатически
|
|
|
dρ |
ν |
|
|
|
ρ (z + |
z) = ρ |
|
(z) + |
|
z , |
(1.72а) |
|
|
|
|
|||||
ν |
|
ν |
|
dz |
|
||
|
|
|
|
|
|
||
a
а плотность окружающей среды может меняться иначе
dρ
ρ(z + z) = ρ(z) + z . (1.72б)
dz
Если на исходном уровне z плотности выделенного объема и окружающей среды одинаковы ( ρ ν = ρ ), то за счет разности
изменений по вертикали этих плотностей возникает архимедова сила, вызывающая ускорение
|
|
|
g dρ |
dρ |
ν |
|
|
|
|||
G |
|
= |
|
|
|
− |
|
|
z . |
(1.73) |
|
a |
|
|
|
|
|||||||
|
|
ρ dz |
|
dz a |
|
||||||
|
|
|
|
||||||||
В том случае, когда градиент плотности воды в океане равен адиабатическому, архимедова сила равна нулю и плотностная стратификация называется безразличной. Если адиабатический градиент плотности воды больше фактического ( точка а на рис.1.4), т.е. их разность в скобках формулы (1.73) отрицательная, то выведенный из состояния равновесия с уровня z элементарный объем
37
жидкости при опускании ( z > 0 ) приобретает плотность большую, чем окружающая среда, и будет стремиться к дальнейшему
опусканию. При подъеме ( z < 0) этот объем жидкости становится менее плотным по сравнению с окружающей средой и будет всплывать. Стратификация, при которой выведенный из состояния
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
равновесия объем жидкости не стремится вернуться на исходный уровень, называется неустойчивой.
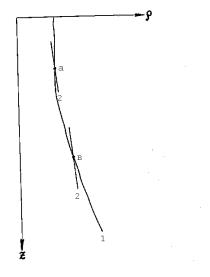
Рис.1.4. Схема соотношения плотностей воды фактической
(1) и потенциальной (2)
при неустойчивой (а) и устойчивой (в) стратификациях.
Если адиабатический градиент плотности меньше фактического (точка в на рис.1.4), т.е. их разность в скобках формулы (1.73) положительная, то выведенный из состояния равновесия объем жидкости старается вернуться на первоначальный уровень, поскольку при подъеме он оказывается плотнее окружающей среды, а при опускании - менее плотным. Такая стратификация называется
устойчивой.
В формуле (1.73) множитель z является произвольным, поэтому его обычно опускают При этом формула приобретает размерность с−2
:
|
|
g dρ |
dρ |
ν |
|
|
|
|||
N 2 |
= |
|
|
|
− |
|
|
. |
(1.74) |
|
|
|
|
|
|||||||
|
|
ρ dz |
|
dz a |
|
|||||
Параметр N называют частотой Вяйсяля-Брента . Он характеризует частоту инерционных колебаний объема воды, выведенной из состояния равновесия при устойчивой стратификации океана.
При практических оценках стратификации океана удобнее использовать не плотность, а такие измеряемые характеристики, как температура, соленость, давление. Поскольку полагается, что при адиабатическом процессе выделенный объем жидкости не изменяет
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
своей солености, |
его градиент плотности представляется в виде |
||||||||||||
dρ |
ν |
|
∂ρ dT |
∂ρ dP |
|
||||||||
|
|
|
= |
|
|
|
+ |
|
|
|
. |
(1.75) |
|
|
|
|
|
|
|
|
|||||||
dz |
|
∂T dz |
∂P |
dz |
|
||||||||
|
|
|
|
a |
|
|
|
a |
|
|
|
a |
|
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
Градиент плотности окружающей воды описывается выражением
dρ |
∂ρ dT |
∂ρ dS |
∂ρ dP |
|
||||||||||
|
= |
|
|
|
+ |
|
|
|
+ |
|
|
|
. |
(1.76) |
|
|
|
|
|
|
|
||||||||
dz |
∂T dz |
∂S dz |
∂P dz |
|
||||||||||
Подстановка этих двух последних выражений градиентов давления в формулу (1.74) при условии, что из-за быстрого выравнивания давления оно в перемещающемся объеме воды и в окружающей среде одинаково, видоизменяет ее
|
|
|
|
|
dT |
dT |
|
|
|
|
|
|
|||
|
|
g ∂ρ |
|
|
∂ρ dS |
|
|||||||||
N 2 |
= |
|
|
|
|
|
− |
|
|
+ |
|
|
|
. |
(1.77) |
|
|
dz |
|
|
|
||||||||||
|
|
ρ ∂T |
|
dz |
a |
∂S dz |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В таком виде квадрат частоты Вяйсяля-Брента называют критерием устойчивости Хессельберга-Свердрупа. Он используется для характеристики плотностной стратификации океана.
Для того чтобы оценить относительное влияние градиентов температуры и солености на устойчивость вод, достаточно в формуле (1.77) определить по уравнению состояния зависимость плотности воды от температуры и солености, производные которых входят множителями к соответствующим градиентам. Множитель при градиенте солености почти на порядок величины больше, чем при градиенте температуры. Следовательно, несмотря на малые градиенты солености, она оказывает большое влияние на плотностную стратификацию океана. Поэтому в тех акваториях Мирового океана, где происходит распреснение поверхностного слоя за счет стока речных вод, таяния льда и осадков, плотностная стратификация оказывается очень устойчивой и переход к неустойчивому состоянию за счет только одного изменения температуры практически невозможен. Например, в летний период года из-за распреснения при таянии льда в арктических морях градиенты солености достигают значений порядка 0,5 0/00 на 1м. Чтобы преодолеть обусловленную соленостью такую устойчивость, необходим градиент температуры не менее 50C на 1м, что практически никогда не наблюдается.
Из уравнения состояния следует, что знак сомножителя у градиента солености в формуле (1.77) положительный, а у градиента температуры - отрицательный. Поэтому рост солености с глубиной способствует повышению устойчивости, а рост температуры воды с глубиной - уменьшает ее.
Критерий устойчивости очень часто используется в океанологической практике и для удобства его определения составлены Океанографические таблицы [2]. Однако при их использовании следует иметь в виду, что изменения плотности по
39
температуре и солености в них вычислены по уравнению состояния Кнудсена. Если пользоваться другим уравнением состояния морской воды, то значения Ν2 могут отличаться от приведенных в таблицах.
Дополнительная литература
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
1.Мамаев О.И. Термохалинный анализ вод Мирового океана.−Л.: Гидрометеоиздат, 1987. − 296с.
2.Океанографические таблицы. Изд. 4-е.−Л.: Гидрометеоиздат, 1975.−477с.
3.Попов Н.И., Федоров К.Н., Орлов В.М. Морская вода. Справочное руководство. − М.: Наука, 1979.−327с.
4.Савельев И.В. Курс общей физики. Кн.3. Молекулярнаяя физика и термодинамика. Изд. 4-е.−М.: Наука, 1998. − 208с.
5.Трайбус М. Термостатика и термодинамика /Пер. с англ./ −М.: Энергия,
1970.− 501с.
Вопросы для самопроверки
1. Каков физический смысл энергии, энтропии, энтальпии и химического потенциала термодинамической системы морской воды?
2.Что характеризует основное уравнение термодинамики морской воды?
3.В чем различие между дифференциальным уравнением состояния морской воды и уравнениями Кнудсена, УС-80 и другими?
4.Почему различаются изобарическая и изохорная теплоемкости морской воды?
5.Как изменяется энтальпия морской воды при изменении ее фазового состояния? Какова связь с теплотой фазовых переходов?
6.В чем суть адиабатических и изэнтропических процессов и каково их влияние на температуру и плотность воды в океане?
7.Как связана вертикальная устойчивость вод океана с распределением температуры и солености?
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
25
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
26
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
27
Библиотека сайта www.fluger.org
Глава 2
ОСНОВНЫЕ ЗАКОНЫ ИЗМЕНЕНИЯ ТЕРМОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОКЕАНА
2.1.Уравнение движения морской воды
Вода выходит из состояния покоя и начинает двигаться под действием различных сил, которые подразделены на две категории:
объемные, или массовые, и поверхностные. К первой категории принято относить те силы, которые действуют непосредственно на все элементы объема: гравитационные, электромагнитные и т.д. Ко второй относят силы, непосредственно влияющие на поверхность объема массы, а далее это влияние различным способом передается в глубь объема. В эту категорию входят силы трения и давления между объемами жидкости.
При изучении динамики морской воды как сплошной среды рассматриваются не сами объемные силы, а плотность их распределения. Согласно определению, даваемому в механике сплошных сред, под плотностью распределения объемной силы в
точке О понимают предел отношения равнодействующей объемных сил F0, действующих на частицы малого объема ν с центром в точке О, к массе этого объема
F= lim ( F0/ ρ ν ). |
(2.1) |
ν →0 |
|
Размерность F в системе СИ будет Н/кг. или м/с2 . |
|
Поверхностные силы также выражаются плотностью их
распределения Р, но не по объему, а по поверхности П |
|
Р= lim ( Р0/ П ). |
(2.2) |
п→0 |
|
Размерность Р в системе СИ составляет Н/м2.
Величина поверхностной силы зависит от ориентировки площадки, на которую она действует. Чтобы этого избежать, плотность распределения этой силы, которую ради краткости обычно называют просто поверхностной силой, проектируется на координатные плоскости. Из гидромеханики известно, что такая проекция
представляется выражением |
|
|
|
Р dП = Рx d Пx + РY d П y+ Рz d Пz , |
(2.3) |
где |
dПx ,dПy ,dПz - проекции площадки dП на соответствующие |
|
координатные плоскости. Их также можно выражать |
через эту |
|
площадку и косинусы углов наклона к координатным плоскостям
41
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
РdП = Px cos( n,x) dП + Py cos(n,y)dП + Pz cos(n,z)dП. (2.4)
Отсюда следует
P = Px cos(n,x) + Py cos(n,y) + Pz cos (n,z). (2.5)
Часто ради краткости записи это выражение представляют следующим образом
P = Pxnx + Py ny + Pz nz . |
(2.6) |
Из этого соотношения видно, что вектор поверхностной силы в любой точке среды зависит от ориентировки в ней площадки, на которую он действует.
В дальнейшем ради краткости изложения плотности распределения массовых и поверхностных сил называются просто соответствующими силами, как это принято в литературе.
Для того чтобы получить уравнение движения элементарного объема воды, используется закон изменения количества движения,
согласно которому изменение главного вектора количества движения
системы материальных частиц I равно главному вектору внешних массовых и поверхностных сил:
dI/dt = ∫FdM + ∫PdП |
(2.7) |
Главный вектор количества движения для объема ν определяется
интегралом |
от произведения абсолютных |
скоростей Vа |
и |
||||
элементарных масс частиц в объеме |
|
|
|||||
|
|
|
|
I = ∫ |
Va .dM. |
(2.8) |
|
|
|
|
|
ν |
|
|
|
|
Если |
выделенный |
объем |
|
|
||
жидкости |
|
неизменный |
и |
|
|
||
небольшой, позволяющий отнести |
|
|
|||||
отмеченную скорость не только к |
|
|
|||||
его отдельным частям, но и ко |
|
|
|||||
всему объему, то уравнение (2.7) |
|
|
|||||
можно |
переписать в |
виде |
|
|
|||
∫ |
dVa |
dM = ∫FdM + ∫PdП .(2.9) |
|
|
|||
|
|
|
|||||
ν |
dt |
ν |
П |
|
|
|
|
|
|
|
|
|
|||
В океанологии полученное
уравнение без дополнительных преобразований не используется. В первую очередь необходимо
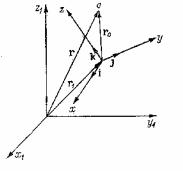
Рис.2.1.Схема положения выделенного объема в неподвижной и неподвижной и подвижной системах координат
перейти от абсолютной скорости движения жидкости к скорости относительно вращающейся Земли.
Для того чтобы учесть ускорение, возникающее за счет вращения Земли, проще всего рассмотреть две системы координат: неподвижную x1, y1, z1 и подвижную x,y,z (Рис.2.1).
42
Библиотека сайта www.fluger.org
Библиотека сайта www.fluger.org
Пусть вектор r определяет положение центра выделенного элементарного объема в первой системе координат, а r0 - во второй. Тогда, если r1 обозначает положение центра подвижной системы координат в неподвижной, можно записать
r = r1 + r0 = r1 + (x i + y j + z k) . |
(2.10) |
Для того чтобы перейти к ускорениям, нужно это выражение дважды продифференцировать по t, в результате чего получается
d |
V |
|
d |
2 r |
|
d |
2 r |
|
d |
2 i |
|
d |
2 j |
|
d |
2 k |
|
|
a |
= |
|
= |
1 |
+ x |
|
+ y |
|
+ z |
|
|
+ |
||||||
|
|
dt 2 |
dt 2 |
dt 2 |
dt 2 |
dt 2 |
||||||||||||
dt |
|
|
|
|
|
|
|
|||||||||||
d 2 x |
|
d 2 y |
|
d 2 z |
dx di |
|
dy dj dz dk |
|
|||||||||||||||
+ |
|
|
i + |
|
|
j + |
|
|
k |
+ 2 |
|
|
|
+ |
|
|
|
+ |
|
|
|
. |
(2.11) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dt |
2 |
|
dt |
2 |
|
dt |
2 |
|
dt dt |
|
dt dt |
dt dt |
|
||||||||||
Как известно, выражение, стоящее в первых скобках правой части этого равенства, определяет переносное ускорение, во вторых скобках - относительное ускорение, в третьих - ускорение Кориолиса. Производные от ортов обычно выражают через угловую скорость вращения подвижной системы, т.е. Земли, ω
di/dt= ω × i , dj/dt = ω × j , dk/dt = ω × k.
После подстановки этих соотношений в уравнение (2.11) и учета
равномерности |
поступательного |
движения Земли, из-за которого |
||||
d2r1/dt2=0,а также с учетом того, что ω = 7,29 10−5 с−1 |
есть величина |
|||||
постоянная, оно приобретает вид |
|
|
||||
|
dVa |
= ω × (ω × r )+ |
dV |
+ 2(ω × V) , |
( 2.12 ) |
|
|
|
|
||||
|
dt |
0 |
dt |
|
|
|
|
|
|
|
|||
где V - скорость движения воды относительно Земли. |
|
|||||
Следующий |
этап преобразований уравнения (2.9) |
сводится к |
||||
замене интеграла от поверхностных сил в объемный на основании теоремы Гаусса-Остроградского и соотношения (2.6)
|
|
|
∂ |
P |
∂P |
y |
|
∂ |
P |
|
1 |
|
∂ |
P |
∂P |
y |
|
∂ |
P |
||||
∫PdП = ∫ |
x |
+ |
|
+ |
z |
dν = ∫ |
|
x |
+ |
|
+ |
z |
dM . |
||||||||||
|
|
∂ y |
|
|
|
|
|
∂ y |
|
|
|||||||||||||
П |
ν |
∂ x |
|
∂z |
ν |
ρ ∂x |
|
∂z |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( 2.13 )
Подстановка выражений (2.12) и (2.13) в уравнение (2.9) приводит его к виду, в котором каждое слагаемое выражено через объемный интеграл. Поскольку объем всех интегралов одинаков и
43
Библиотека сайта www.fluger.org
