
motau
.pdf
5. Составляем |
характеристическое |
|
уравнение |
det( A E) 0 : |
|||
|
3 |
4 |
2 |
5 |
2 |
0 . |
|
7.Находим корни характеристического уравнения:
|
1 |
2; |
2 |
|
3 |
1; (корни вещественные: два |
из них кратные). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
Для корня |
1 |
|
2 |
найдем частное решение вида: |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x (t) |
|
h(1) |
e2t ; |
x (t) h(1) |
2 |
e2t |
x (t) |
h(1) |
e2t . |
|
|
|
|
1 |
|
|
1 |
|
2 |
|
3 |
3 |
|
|
Для этого найдем собственный вектор h(1). Это можно сделать двумя способами:
а) решить систему однородных алгебраических уравнений (2.7), под-
ставляя значение корня |
1 |
2 : |
|
|
|
|
|
|
|
|
|
|
6 |
h11 |
2 h12 |
5 h13 |
0 |
|
6 h11 |
3 h12 |
6 h13 |
0 ; |
|
|
8 |
h11 |
3 h12 |
7 h13 |
0 |
б) вычислением алгебраических дополнений элементов первой строки определителя det |А- Е | с подстановкой значения корня 1 2 :
|
|
|
|
|
2 |
8 |
9 |
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
11 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h(1) k |
|
k |
6 |
|
6 |
|
|
6 |
2 . |
|
|
|||||||
12 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
10 |
8 |
|
|
6 |
2 |
|
|
|
|
||||
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
частное |
решение |
для значения |
|
корня |
1 |
2 |
запишется: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
2 |
(t) 1 e |
2t |
; x2 |
2 |
(t) |
2 e |
2t |
; x3 |
2 |
(t) 2 e |
2t |
. |
|
(2.11) |
|||
|
|
|
|
|
|
|
|
|||||||||||
81

9. Найдем частное решение для корня =1 (кратности 2):
1) определим число линейно независимых собственных векторов. При
подстановке |
значения корня |
=1 в выражение (А- |
Е) получим матри- |
||||||||||||||||||
цу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( A |
|
|
E) |
6 |
|
2 |
|
6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
3 |
|
8 |
|
|
|
|
|
|
|
|
|
Ее порядок n равен 3 , ранг |
r= 2, |
найденный известными метода- |
|||||||||||||||||
ми. |
|
Число |
линейно |
независимых |
собственных |
векторов |
равно |
||||||||||||||
m |
n r 1. Корень |
=1 имеет кратность k=2. |
|
|
|
|
|
|
|
||||||||||||
|
|
Так как m<k, |
то решение следует искать в виде произведения мно- |
||||||||||||||||||
гочлена степени k-m=1 на |
e1t : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x1(t) |
P(1) (t) |
e1t |
(a1 |
a2 |
t) |
e1t ; |
x2 (t) |
|
Q(1) (t) |
e1t |
|
(b1 |
b2 |
t) e1t ; |
|
||||||
x3(t) |
S (1) (t) |
e1t |
(c1 |
c2 |
t) |
e1t . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Для нахождения коэффициентов ai, |
bi, ci |
(i=1,2) делаем подстанов- |
|||||||||||||||||
ку полученных выражений в исходную систему (2.4). |
|
|
|
|
|||||||||||||||||
|
|
Сокращая на |
e1 t правую |
и левую |
часть |
уравнений, |
имеем: |
||||||||||||||
|
|
|
a2 t a1 |
a2 |
( 4a2 |
2b2 |
|
5c2 ) t 4a1 |
2b1 |
5c1 |
|
|
|||||||||
|
|
|
b2 t b1 |
b2 |
|
(6a2 |
b2 |
|
6c2 ) t 6a1 |
|
b1 |
6c1 . |
|
|
|||||||
|
|
|
c2 t c1 |
c2 |
( 8a2 |
3b2 |
|
9c2 ) t 8a1 |
|
3b1 |
9c1 |
|
|
||||||||
|
|
Приравнивая |
коэффициенты |
при |
t |
и свободные члены, получаем |
|||||||||||||||
систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Так как кратность корня |
=1 |
равна 2, будем считать известными |
|||||||||||||||||
два коэффициента с1 и с2 . Остальные неизвестные коэффициенты |
вы- |
||||||||||||||||||||
разим через них. Решая систему, находим: |
a2 |
c2 ; |
a1 |
c1 |
c2; |
b2 |
0; |
||||||||||||||
b1 |
3 c2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82

5 a |
2 b 5 c |
0, |
(t1) |
|
2 |
2 |
2 |
|
|
5 a 2 b 5 c a , |
(t0 ) |
|||
1 |
1 |
1 |
2 |
|
6 a |
2 b 6 c |
0, |
(t1) |
|
2 |
2 |
2 |
|
|
6 a 2 b 6 c b , |
(t0 ) |
|||
1 |
1 |
1 |
2 |
|
8 a |
3 b 8 c |
0, |
(t1) |
|
2 |
2 |
2 |
|
|
8 a 3 b 8 c c . |
(t0 ) |
|||
1 |
1 |
1 |
2 |
|
Частное решение для кратного корня |
=1 принимает вид: |
|||
x |
1(t) |
(c |
c |
c |
t) et |
; x |
1(t) 3 c et |
; |
1 |
|
1 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
et. |
|
|
(2.12) |
x |
1(t) |
(c |
c t) |
|
|
|
||
3 |
|
1 |
2 |
|
|
|
|
|
Общим решением исходной системы будет сумма решений (2.11), умноженного на с3, и (2.12):
x1(t) x1 |
1(t) x1 |
2 (t) (c1 |
c2 c3 t) et c3 e2t ; |
||
x2 (t) x2 |
1(t) x2 |
2 (t) 3 c2 et 2 c3 e2t ; |
|||
x3(t) x3 |
1(t) x3 |
2 (t) (c1 |
c2 t) et 2 c3 e2t , |
||
где c1, c2 , c3 , – постоянные интегрирования, находящиеся из начальных условий.
Пример 3
Найти решение системы дифференциальных уравнений
|
|
dx1 |
|
5 x1 |
x2 |
|
|
|
dt |
|
|
||
|
|
|
|
|
|
|
|
dx2 |
|
x1 |
5 x2 |
|
|
|
|
dt |
|
|
||
|
|
|
|
|
|
|
с начальными условиями X0 |
x0,1 . |
|||||
|
|
|
|
|
|
x0,2 |
Решение
1.Составляем матрицу коэффициентов:
83

A5 1 .
1 5
2.Составляем лямбда-матрицу (А- Е):
|
|
|
|
|
|
A |
5 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
1 |
5 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Составляем и решаем характеристическое уравнение: |
|
|||||||||||
|
|
|
|
|
|
2 |
10 |
26 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1,2 |
5 |
i |
(корни комплексно сопряженные). |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Для |
корня |
|
5 |
i |
найдем |
собственный |
вектор |
h(1) . |
||||
Для этой цели |
делаем подстановку в матрицу ( A |
E) |
значения этого |
||||||||||
корня и получаем систему уравнений: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
i |
h11 |
h12 |
0 |
|
|
|
|
|
|
|
|
|
|
h11 |
i |
h12 |
0 . |
|
|
|
|
Эти |
два |
уравнения |
линейно |
зависимы. |
Поэтому |
для нахождения |
|||||||
h11 и h12 можно |
воспользоваться любым уравнением системы. |
Пусть |
|||||||||||
h11 |
1. Тогда из первого уравнения h12 |
i . |
|
|
|
|
|||||||
5. Частное решение запишется следующим образом (последние преобразования по формуле Эйлера):
x1(t) |
1 e(5 i) t |
h1 e(5 i)t |
e5t |
eit |
e5t |
(cos(t) i |
sin(t)) ; |
x2 (t) |
h2 e(5 i)t |
i e(5 i) t |
i |
e5t |
eit |
e5t (sin(t) |
i cos(t)) . |
Так как данная система имеет вещественные коэффициенты, то решение, соответствующее корню 5 i , можно не искать – оно будет комплексно сопряженным с найденным решением.
6.Записываем решение в вещественной форме. Для этой цели вы-
деляем в комплексном решении x1 и x2 два вещественных линейнонезависимых решения, отделяя в них вещественную и мнимую части:
84

x |
Re(x ) |
e5t |
cos(t) |
|
|
11 |
1 |
|
|
|
(первое частное решение); |
|
|
e5t |
|
|
|
x |
Re(x ) |
sin(t) |
|
||
12 |
2 |
|
|
|
|
x |
Im(x ) |
e5t |
|
sin(t) |
|
21 |
1 |
|
|
|
(второе частное решение). |
|
|
e5t |
|
||
x |
Im(x ) |
cos(t) |
|
||
22 |
2 |
|
|
|
|
7. Общее решение выражается через два найденных линейнонезависимых решения (с1 и с2 определяются вектором начальных условий):
|
|
|
|
x1 |
c1 |
x11 |
c2 |
x12 |
e5t (c1 cos(t) |
c2 sin(t)); |
|
|
|||||||||
|
|
|
|
x2 (t) c1 |
x12 |
|
c2 |
x22 |
e5t (c1 sin(t) |
c2 cos(t)). |
|
|
|||||||||
|
|
|
|
|
|
Задания практического занятия № 5 |
|
|
|||||||||||||
Дана система дифференциальных уравнений: |
|
|
|
|
|
|
|||||||||||||||
|
|
dx1 |
|
a11 x1 |
a12 |
x2 |
a13 x3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dx2 |
|
a21 x1 |
a22 |
x2 |
a23 x3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dx3 |
|
a31 x1 |
a32 |
x2 |
a33 x3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x10 |
|
|
|
|
|
|
|
|
|
|
|
||
с начальными условиями x20 . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x30 |
|
|
|
|
|
|
|
|
|
|
|
||
Требуется: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
решить систему уравнений и построить графики зависимостей |
|
|
|||||||||||||||||||
x1(t), x2 (t) |
x3(t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Варианты практического занятия № 5 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вари- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анты |
|
a11 |
a12 |
|
а13 |
|
a21 |
|
а22 |
|
а23 |
а31 |
а32 |
а33 |
|
x10 |
|
x20 |
x30 |
||
зада- |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
-4 |
-3 |
|
-2 |
|
0 |
|
0 |
|
1 |
6 |
5 |
2 |
|
1 |
|
1 |
2 |
|||
2. |
8 |
|
2 |
|
-1 |
|
0 |
|
1 |
|
-1 |
-6 |
-4 |
1 |
|
1 |
|
2 |
0 |
||
3. |
-2 |
2 |
|
-1 |
|
0 |
|
-5 |
|
-1 |
-6 |
-4 |
1 |
|
1 |
|
2 |
0 |
|||
85
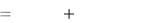
Варианты практического занятия № 5 (продолжение)
Вари- |
|
|
|
|
|
|
|
|
|
|
|
|
|
анты |
a11 |
a12 |
а13 |
a21 |
а22 |
а23 |
а31 |
а32 |
а33 |
x10 |
x20 |
x30 |
|
зада- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ния |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
-2 |
2 |
-1 |
6 |
0 |
-1 |
2 |
-4 |
1 |
1 |
2 |
0 |
|
5. |
-4 |
-3 |
-2 |
0 |
0 |
1 |
6 |
5 |
2 |
1 |
0 |
2 |
|
6. |
9 |
2 |
1 |
-6 |
5 |
1 |
7 |
-4 |
1 |
1 |
1 |
2 |
|
7. |
-1 |
0 |
4 |
3 |
2 |
1 |
1 |
1 |
6 |
1 |
0 |
2 |
|
8. |
1 |
2 |
-1 |
8 |
1 |
-1 |
1 |
-4 |
1 |
1 |
0 |
0 |
|
9. |
2 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
2 |
1 |
0 |
2 |
|
10. |
-8 |
-2 |
1 |
0 |
-1 |
1 |
6 |
4 |
-1 |
0 |
0 |
2 |
|
11. |
-4 |
-3 |
-2 |
0 |
0 |
1 |
6 |
5 |
2 |
1 |
0 |
2 |
|
12. |
-2 |
2 |
1 |
0 |
-5 |
-1 |
-6 |
-4 |
1 |
1 |
0 |
1 |
|
13. |
-2 |
2 |
-1 |
6 |
0 |
-1 |
2 |
-4 |
1 |
2 |
1 |
2 |
|
14. |
-1 |
0 |
4 |
3 |
2 |
1 |
1 |
1 |
6 |
1 |
1 |
2 |
|
15. |
-8 |
-2 |
1 |
0 |
-1 |
1 |
6 |
4 |
-1 |
1 |
1 |
2 |
|
16. |
2 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
2 |
2 |
1 |
2 |
|
17. |
1 |
2 |
-1 |
8 |
1 |
-1 |
1 |
-4 |
1 |
1 |
1 |
2 |
|
18. |
9 |
2 |
1 |
-6 |
5 |
1 |
7 |
-4 |
1 |
1 |
2 |
1 |
|
19. |
-2 |
2 |
-1 |
6 |
0 |
-1 |
2 |
-4 |
1 |
1 |
2 |
1 |
|
20. |
8 |
2 |
-1 |
0 |
1 |
-1 |
-6 |
-4 |
1 |
1 |
2 |
1 |
2.2. РЕШЕНИЕ НЕОДНОРОДНОЙ СИСТЕМЫ ДИФФЕРНЦИАЛЬНЫХ УРАВНЕНИЙ
Практическое занятие № 6
Основные положения
Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид:
|
dX |
AX (t) G(t). |
(2.13) |
|
|
|
|
|
dt |
|
|
|
|
|
|
Решение системы (2.13) состоит |
из суммы двух решений: |
||
общего решения однородной системы уравнений (см. раздел 2.1) и частного решения. Рассмотрим методы нахождения частного решения системы дифференциальных уравнений.
86

Метод вариации произвольных постоянных (метод Лагранжа)
Этим методом можно построить общее решение неоднородной системы (2.13) , исходя из фундаментальной системы решений соответствующей однородной системы.
Согласно методу Лагранжа частное решение системы (2.13) получается в виде:
X (t) e A t X |
0 |
t e A(t ) |
G( ) d . |
(2.14) |
|
0 |
|
|
|
|
|
|
|
Полученный результат рассматривается как сумма решений соответствующей однородной системы дифференциальных уравнений и частного решения неоднородной системы.
Метод неопределенных коэффициентов
Частное решение неоднородной линейной системы возможно получить этим методом, если функция G(t) представлена в виде произве-
дения экспоненциальной функции на алгебраический полином (или на гармоническую функцию).
1. Элементы вектора G(t) можно представить в виде произведения полинома степени m на экспоненциальную функцию:
|
|
|
g |
k |
(t) Pmk ev t , (k 1, 2, , n) , |
|
|||||
|
|
|
|
|
|
k |
|
|
|
|
|
где |
Pmk (t) |
a |
a |
|
t |
a |
tmk |
(k |
1, 2, , n) полином степе- |
||
|
k |
0k |
|
1k |
|
mk |
|
|
|
|
|
ни m. |
|
|
|
|
|
|
|
|
|
|
|
Частное решение в этом случае отыскивается в виде: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
(2.15) |
|
|
xkчастн (t) |
|
|
Qkz |
s (t) ev t |
(k |
1, 2, |
, n) , |
|
|
где Qz |
s (t) – полиномы степени (m+s) с неизвестными коэффициен- |
||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
тами; |
z m a x (m |
) |
|
k( |
1, 2 , n ,– максимальная) |
степень полинома |
|||||
|
|
k |
|
|
|
|
|
|
|
|
|
gk (t) ; |
v – экспоненциальная степень полинома gk (t) ; s –коэффициент. |
||||||||||
Величина s находится из следующих условий:
87

а) s =0 , если v не является корнем характеристического уравнения однородной системы;
б) s= k (k – кратность корня), если v является корнем характеристического уравнения однородной системы.
Неизвестные коэффициенты полиномов определяются путем подстановки выражения (7) в систему (6) и приравниванием коэффициен-
тов при подобных членах уравнений. |
|
||||
2 . Элементы вектора G(t) |
представлены в виде |
произведения поли- |
|||
номов степени mk ,nk на гармонические функции: |
|
||||
g |
k |
(t) |
e t Rmk (t) cos( |
t) W nk (t) sin( t) . |
(k 1, 2, , n) |
|
|
k |
k |
|
|
Частное решение запишется в этом случае:
|
частн |
(t) e |
t |
z |
s |
(t) |
z |
s |
(t) |
sin( t) , |
(2.16) |
|
|
xk |
|
Pk |
|
cos( t) Qk |
|
|
|||||
где Pz |
s , Qz |
s |
– полиномы степени (z+s) с неизвестными |
коэффици- |
||||||||
k |
k |
|
|
|
|
|
|
|
|
|
|
|
ентами; z max (mk |
|
n, k ) |
|
k( |
1, 2, n , –)максимальная степень поли- |
|||||||
нома gk (t) ; |
( |
i ) |
– экспоненциальная степень полинома |
gk (t) ; s – |
||||||||
коэффициент. |
|
|
|
|
|
|
|
|
|
|
|
|
Величина s находится из следующих условий: |
|
|||||||||||
а) |
s =0 |
, |
если |
|
|
i |
не является корнем характеристического |
|||||
уравнения однородной системы; |
|
|
|
|
||||||||
б) s= k (k – кратность корня), если |
|
i |
является корнем характе- |
|||||||||
ристического уравнения однородной системы.
Неизвестные коэффициенты полиномов определяются путем подстановки выражения (2.15) или (2.16) в систему дифференциальных уравнения (2.13) и приравниванием коэффициентов при подобных членах уравнений.
Пример 1
Найти общее решение системы методом Лагранжа
dx1 |
|
2 |
X 2 |
3 t |
||
dt |
||||||
|
|
|
||||
|
dx2 |
2 |
X1 |
4 |
||
|
dt |
|||||
|
|
|
|
|||
88
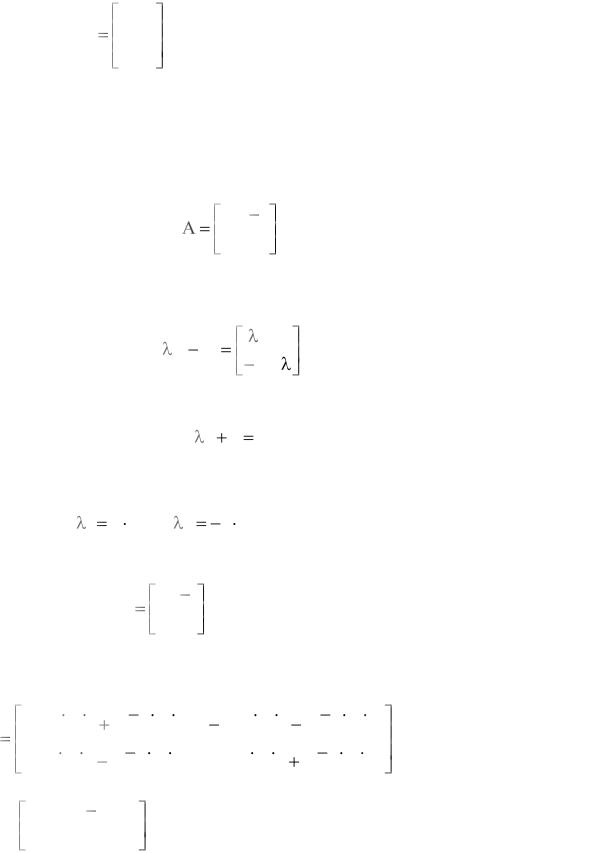
с нач. усл.: X0 |
x1,0 . |
|
x2,0 |
Решение
1. Находим общее решение однородной системы уравнений: а) матрица коэффициентов
0 2 ;
2 0
б) характеристическая матрица:
|
|
|
|
|
E |
A |
|
2 |
; |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
в) характеристическое уравнение: |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
2 |
4 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) корни характеристического уравнения: |
|
||||||||||
|
1 |
2 i ; |
|
|
2 |
|
2 i |
(корни мнимые); |
|
||
|
|
|
|
|
|
|
|
|
|||
д) модальная матрица: |
|
|
|
|
|
|
|
|
|||
|
|
H |
i |
i |
; |
|
|
|
|
||
|
|
|
1 |
1 |
|
|
|
|
|
||
е) фундаментальная матрица: |
|
|
|
|
|
||||||
Ф(t) |
i(e(2 i) t |
e( 2 i) t ) |
|
(e(2 i) t |
e( 2 i) t ) |
= |
|||||
(e(2 i) t |
e( 2 i) t ) |
i(e(2 i) t |
e( 2 i) t ) |
||||||||
|
|
||||||||||
= |
cos2t |
sin 2t |
; |
|
|
|
|
|
|
|
|
|
sin 2t cos2t |
|
|
|
|
|
|
|
|
||
89

ж) общее решение однородной системы:
|
x1,0 cos 2t |
x2,0 sin 2t |
|
общ |
(t) |
|
. |
|
x1,0 |
sin 2t |
x2,0 cos 2t |
2. Находим частное решение системы по формуле (2.14), преобразовывая ее следующим образом:
t
X (t) (t) Ф 1( ) G( )d .
0
Для этого производим следующие операции: а) обращаем матрицу Ф(t):
|
|
1(t) |
cos 2 |
sin 2 |
; |
|
|
||
|
|
|
sin 2 |
cos 2 |
|
|
|||
|
|
|
|
|
|
|
|||
б) перемножаем матрицы Ф-1(t) и G(t): |
|
|
|
||||||
1( ) G( ) |
cos2 |
sin 2 |
3 |
3 cos2 |
4 sin 2 |
; |
|||
sin 2 |
cos2 |
4 |
3 sin 2 |
4 cos2 |
|||||
|
|
||||||||
в) берем интеграл от полученного вектор-столбца (по частям):
t |
t |
|
( ) G( )d |
0 |
0 |
|
|
|
|
3 |
|
t cos 2t |
|
5 |
cos 2t |
|
||
3 |
cos 2 |
4 sin 2 |
d |
2 |
|
|
4 |
; |
||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||
3 |
sin 2 |
4 cos 2 |
|
3 |
|
5 |
|
|
|
|||
|
cos 2t |
|
sin 2t |
|
||||||||
|
|
|
|
2 |
4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
г) умножаем фундаментальную матрицу на полученный интегрированием вектор и вычисляем частное решение системы:
|
t |
|
|
|
5 |
cos 2t |
3 |
sin 2t |
5 |
||||
|
|
cos 2t |
sin 2t |
4 |
2 |
4 |
|||||||
x (t) eAt |
e A |
g( ) d |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
част |
|
|
sin 2t |
cos 2t |
5 |
|
3 |
|
|
||||
|
|
|
|
cos 2t |
|
||||||||
|
0 |
|
|
|
|
4 sin 2t |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90
