
Posobb
.pdf
Следовательно, существует достаточно малая окрестность точки =с с радиусом , в которой нули dk и qk, k=N, N+1, N+2,…, совпадают, функция () не имеет в этой окрестности полюсов и является аналитической.
С другой стороны, при k<N нули dk и qk лежат вне окрестности точки =с с радиусом , их конечное число, они не совпадают и точки = dk k=1,2,…,N-1 являются изолированными полюсами функции ( ).
3.3. Устойчивые квазимногочлены
Определение 3.11. Квазимногочлен D() называют устойчивым, если все его нули = , =1,2,..., расположены на комплексной плоскости слева от мнимой оси, то есть
|
|
Re 0, |
1,2,..., |
|
|
|
|
Определение 3.12. Если для квазимногочлена |
|||
D( ) A () n A () n 1 |
... A () , |
A () 0 |
|
0 |
1 |
n |
0 |
существует такое действительное число , что имеет место
|
lim |
D( ) |
ca const , <M< , |
|
|||
|
|
|
|||||
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то число будем называть приращением степени квазимногочлена D( )
при | |, <M< , .
Заметим, что определение приращения степени квазимногочлена при
| | будем понимать в асимптотическом смысле. Обозначим =+i и положим < , | |. Тогда
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
2 |
|
2 |
e |
i при , < . |
|||||||||
|
|||||||||||||||
|
|
exp arctg |
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Принимая =i, получаем |
lim |
D(i) |
const . Определение значения |
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
(i)n |
|
|||||
сводится к вычислению и построению на ПЭВМ частотного годографа
D(i ) |
и выбору такого действительного числа |
, при котором |
|
|
|||
(i )n |
|||
|
|
||
D(i) |
const при . |
|
|
|
|
||
(i)n |
|
||
|
|
Определение 3.13. Если в квазимногочлене D() положить =i , то выражение
D(i ) u() iv() A0 (i )(i )n A1(i )(i )n 1 ... An (i)
называют частотной характеристикой квазимногочлена D( ).
Определение 3.14. Частотным годографом квазимногочлена D( ) называют кривую L, которую описывает конечная точка вектора
61
D(i ) u() iv() на комплексной плоскости (u, iv) при монотонном
возрастании от - до +.
Теорема 3.5 (теорема об устойчивых квазимногочленах)
Пусть переменные коэффициенты Aj( ), j=0,1,...,n |
квазимногочлена |
||
D( ) A () n A () n 1 |
... A () , |
A () 0 , |
|
0 |
1 |
n |
0 |
являются аналитическими функциями в правой половине и на мнимой оси комплексной плоскости =+i и выполняются условия:
существует действительное число такое, что
0 : lim |
D( ) |
Ca 0; |
(3.43) |
|||
|
|
|||||
|
n |
|||||
|
|
|
|
|
|
|
( , ) : D(i) u( ) iv( ) 0, u( ) u( ), v( ) v( ) (3.44)
Тогда, если при монотонном возрастании от 0 до вектор D(i ) по-
вернётся на комплексной плоскости (u, iv) от положительной действитель- |
||||||
|
i |
|
|
ной полуоси u в положительном направлении на угол |
||
|
|
|
||||
|
|
|
(n ) , то все нули квазимногочлена |
D() будут |
||
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
r |
|
|
расположены на комплексной плоскости |
слева от |
|
|
|
|
мнимой оси. |
|
||
|
|
|
|
|
||
|
|
|
|
|
Доказательство. Возьмём на комплексной плоско- |
|
0 |
|
|
|
|||
|
сти |
=+i открытую область G, ограниченную за- |
||||
|
G |
|
|
|||
|
|
|
мкнутым контуром (рис. 3.6) S=S1+S2, где S1 - полу- |
|||
S2 |
|
|
|
|||
S1 |
|
|
окружность с центром в точке О и радиусом r в правой |
|||
|
|
|
||||
|
|
|
полуплоскости; S2 - отрезок [-ir; ir]. |
|
||
|
|
|
|
|
||
|
Рис. 3.6 |
|
|
|
По условиям теоремы функция D() аналитична в |
|
|
|
|
области G и при r не имеет нулей на контуре S. |
|||
|
|
|
|
|||
Следовательно, согласно принципу приращения аргумента при однократном полном обходе точкой контура S против часовой стрелки функция D() получает приращение аргумента
lim S arg D( ) |
lim S arg D() |
lim S 2 arg D() 2 N |
(3.45) |
|||||||
r |
r |
1 |
r |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где N – число нулей функции D() в правой половине комплексной плоскости.
С учётом (3.43) имеем
|
|
lim S |
arg D( ) |
|
lim |
|
S arg |
|
|
n D() |
|
|
|
lim S arg |
n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
r |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
S |
|
D() |
|
|
|
|
|
)(S |
arg ) S |
|
|
|
D() |
||||||||||||||||||||||||
lim |
arg |
|
|
|
|
|
|
|
|
lim (n |
arg |
lim |
|
|
|
|||||||||||||||||||||||||
|
|
n |
|
|
|
n |
|
|||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
1 |
|
|
|
|
|
|
r |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(n ) S |
arg ca |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
S |
arg D() (n ) |
|
|
|
(3.46) |
|||
r |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как S2 : |
i , |
то с учётом условия (см. (3.44)) |
u(-)=u( ), |
||||||
v(-)=–v(), запишем |
|
|
|
|
|
|
|||
lim |
S |
arg D( ) lim arg D(i) |
|
|
|
||||
r |
|
2 |
|
r |
r r |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
lim arg D(i ) lim arg D(i ) lim 2arg D(i) |
(3.47) |
||||||||
r |
r |
r |
|
r |
r r |
|
r |
0 r |
|
|
|
|
|
|
|
||||
2 arg D(i) |
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
Подставляя (3.46), (3.47) в (3.45) и принимая N=0, получаем условие |
|||||||||
расположения нулей (корней) квазимногочлена D() на комплексной плос- |
|||||||||
кости слева от мнимой оси, то есть усло- |
|
iv |
|
||||||
вие устойчивости квазимногочлена D( ) |
=r |
|
=0 |
||||||
arg D(i ) (n ) |
|
|
|
|
|||||
|
(3.48) |
|
|
||||||
|
|
|
|
||||||
0 |
|
|
2 |
|
|
|
|
|
|
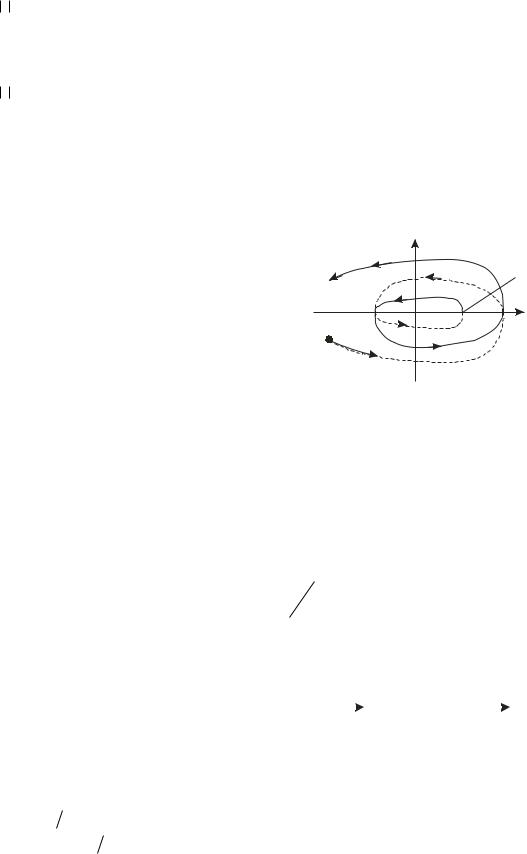
Пояснение. |
Геометрический |
смысл |
|
|
u |
||||
равенства |
|
|
|
|
|
= -r |
|
|
|
arg D(i ) 2 arg D(i) |
|
|
|
|
|||||
|
|
|
|
|
|||||
r r |
|
0 r |
|
|
|
Рис. 3.7 |
|
||
показан на рис. 3.7 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||
3.4. Физически возможные квазирациональные дроби
Пусть некоторая одномерная линейная стационарная динамическая система Ф преобразует входную функцию x(t) в выходную функцию y(t).
Динамическая система Ф задана передаточной функцией в форме ква-
зирациональной дроби
() Q() D()
На рис. 3.8 приведена структурная схема данной линейной одномерной
КДС, где x() и y( ) – Лапласовы изобра- |
|
|
|
||||
жения функций x(t) и y(t) соответственно. x( ) |
|
y( ) |
|||||
( ) |
|||||||
Определение |
3.15. Передаточная |
|
|
|
|||
|
|
||||||
функция называется обобщенной, если она |
|
|
|
||||
|
|
|
|||||
представлена в |
виде квазирациональной |
Рис. 3.8 |
|||||
дроби. |
|
|
|
|
|
|
|
Определение |
3.16. |
Если |
|
|
|
||
( ) Q( ) D( ) есть квазирациональная дробь, то выражение |
|||||||
Ф(i ) Q(i ) D(i) ReФ(i) ImФ(i) |
(3.49) |
||||||
|
|
|
|
63 |
|||
будем называть частотной характеристикой квазирациональной дроби Ф().
Замечание 3.5. Согласно данному определению, частотная характеристика квазирациональной дроби является обобщенной частотной характеристикой соответствующей комбинированной динамической системы.
Пусть x(t) и y(t) абсолютно интегрируемые функции на интервале (- ,+ ). Тогда спектральная характеристика y(i ) выходной функции y(t) имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(i ) (i )x(i ) , где x(i ) x(t)e i t dt |
|
(3.50) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя обратное интегральное преобразование Фурье, находим |
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
|
Ф(i )x(i )ei t d |
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
ReФ(i )cos t ImФ(i )sin t |
|
Re x(i) |
|
||||||||
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ReФ(i )sin t ImФ(i )cos t |
Im x(i ) |
d |
|||||
|
|
|
|
i |
|
|
|
|
|
ReФ(i )cos t ImФ(i )sin t |
Im x(i) |
|
||||||||
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ReФ(i )sin t ImФ(i )cos t |
Re x(i ) |
|
d |
|
|||||||||||||||
В физически возможной системе выходная функция y(t) должна быть вещественной функцией от вещественной переменной t. Для этого достаточно, чтобы
ReФ(i) ReФ(i), |
ImФ(i) ImФ(i) |
При этих условиях в первом интеграле предыдущего выражения подынтегральная функция есть четная функция от , а во втором интеграле
– нечетная функция от , и второй интеграл равен нулю. Следовательно,
y(t) |
1 |
|
|
|
Re (i )cost Im (i )sin t |
|
Re x(i) |
|
||||
2 |
|
|
||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Re (i )sin t Im (i )cost |
|
|
Im x(i ) |
|
d |
||
Положим, что x(t) (t), где (t) – дельта-функция Дирака. Тогда
Re x(i ) Re (i ) 1, Im x(i ) Im (i) 0,
64

|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) q(t) |
|
ReФ(i )cos t ImФ(i )sin t d |
|
|
|
||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исходя из условия q(-t)=0, имеем |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Re (i )cos td Im (i )sin td |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
q(t) |
|
Re (i )cos td |
Re (i )cos td , t 0. |
|
(3.51) |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
Пусть |
|
|
существуют |
|
|
действительные числа |
|
и |
|
такие, что |
|||||||||||
|
lim |
D() |
с |
const , |
lim |
Q() |
с |
const , где |
n, |
m, |
и , |
– |
соответ- |
|||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
n |
|
|
a |
|
|
|
|
|
|
m |
b |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ственно степени и приращения степеней квазимногочленов D() и Q() при |
||||||||||||||||||||||||
. |
|
В |
физически возможной |
дискретно-континуальной |
системе |
|||||||||||||||||||
начальное значение импульсной переходной функции равно нулю, то есть
lim q(t) 0
t 0
Так как q() ( ) Q( )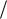 D( ) , то по известной из операционного
D( ) , то по известной из операционного
исчисления формуле начального значения оригинала должно выполняться равенство
lim q(t) lim q( ) lim |
Q( ) |
lim m n 1 |
Q() m |
|
|||||||||||||
D() |
D() n |
||||||||||||||||
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||||
cb lim m n 1 0
ca
Следовательно, n + > m + + 1, |cb| < , ca 0 |
(3.52) |
|
Предложение 3.5. Если выполняются условия |
|
|
ReQ(-i)=ReQ(i), |
ImQ(-i)= –ImQ(i), |
|
ReD(-i)=ReD(i), |
ImD(-i)= –ImD(i), |
|
то следует (проверьте)
Re (-i)=Re (i), Im (-i)= –Im (i),
Определение.3.17. Всякую квазирациональную дробь ( ) Q( )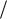 D( ) будем называть физически возможной, если
D( ) будем называть физически возможной, если
Re (-i)=Re (i), Im (-i)= –Im (i), n + > m + + 1, |cb| < , ca 0
65

3.5. Устойчивые квазирациональные дроби
Определение 3.18. Импульсной переходной функцией q(t) физически возможной квазирациональной дроби Ф( ) будем называть выражение
q(t) |
1 0 |
i e t ()d |
, |
|
a, |
t 0, |
(3.53) |
|
|
|
0 |
||||||
|
2i |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
|
где a – абсцисса абсолютной сходимости интеграла Лапласа (1.33). Определение 3.19. Весовой функцией квазирациональной дроби Ф()
будем называть выражение
q(t ) |
1 0 |
i e (t ) ()d |
, |
|
a, |
t 0 |
|
|
|
0 |
|||||
|
2i |
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
i |
|
|
|
|
|
Определение 3.20. Квазирациональная дробь называется устойчивой (неустойчивой), если ее импульсная переходная функция q(t) удовлетворяет (не удовлетворяет) условию
(3.54)
Определение 3.21. Квазирациональная дробь называется асимптотически устойчивой, если ее импульсная переходная функция q(t) удовлетворяет условиям
t 0 : |
|
q(t) |
|
M , |
lim q(t) 0 |
(3.55) |
|
|
|||||
|
|
|
|
|
t |
|
Теорема 3.6. Всякая физически возможная квазирациональная дробь ( )=Q( )/D() является асимптотически устойчивой, если квазимногочлен D() устойчивый, а квазимногочлен Q( ) аналитичен на мнимой оси и в правой половине комплексной плоскости ( ).
Доказательство. Пусть квазимногочлен D() устойчивый, и все его нули расположены слева от мнимой оси на комплексной плоскости ( ). В силу этого все особенности функции e t ( ) лежат слева от мнимой оси и путь интегрирования в формуле Меллина (3.53) проходит по мнимой оси, то есть полагаем 0=0 и =i. Следовательно, из (3.53) имеем
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
q(t) |
|
|
|
(i ) ei t d |
|
|
|
(i ) |
|
d , |
t0 |
(3.56) |
||
|
|
|
||||||||||||
|
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как () по условию теоремы является физически возможной квазирациональной дробью, то с учетом (3.52) получаем
|
lim |
|
(i) |
|
lim |
|
Q(i ) |
|
|
cb |
|
|
lim |
|
1 |
0 , |
(3.57) |
||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
D(i ) |
ca |
|
i |
|
n m |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+–m–>1
Заметим, что функция () не имеет особенностей на мнимой оси. Следовательно,
66

(i) |
|
|
(3.58) |
|
|||
|
|
|
|
Легко видеть, что в соответствии с (3.57) и (3.58) функция (i) абсолютно интегрируема, то есть существует такое M>0, что
1 |
|
|
|
|
|
|
(i ) |
d M |
(3.59) |
||
2 |
|||||
|
|
||||
|
|
|
|
|
Всилу абсолютной интегрируемости функции (i ) по лемме Римана
[18]имеем
lim (i ) ei t d 0
t
Из (3.56), (3.59), (3.60) следует
t 0 : |
|
q(t) |
|
M , |
lim |
|
q(t) |
|
0 |
(3.60) |
|
|
|
|
|||||||
|
|
|
|
|
t |
|
|
|
|
|
и квазирациональная дробь () согласно определению 3.21 асимптотически устойчивая. Что и требовалось доказать.
Теорема 3.7. Если в квазирациональной дроби ( )=Q( )/D( ) квазимногочлен D() имеет в правой половине комплексной плоскости () хотя бы один корень, не совпадающий с корнями квазимногочлена Q(), то квазирациональная дробь () неустойчивая.
Доказательство. Предположим противное, то есть D() имеет в правой половине комплексной плоскости ( ) корень, не совпадающий с корнями Q(), и при этом квазирациональная дробь () устойчивая. Так как ( ) устойчива, то ее импульсная переходная функция q(t) должна удовлетворять условию
t 0 : |
|
q(t) |
|
M |
(3.61) |
|
|
Следовательно, функция (), являющаяся изображением Лапласа оригинала q(t), аналитична при Re >0 (согласно теореме о существовании интеграла Лапласа). Однако в силу того, что знаменатель D() имеет в правой половине плоскости ( ) корень, отличный от корней числителя Q(), квазирациональная дробь ( )=Q( )/D() имеет в правой полуплоскости ( ) особенности. Но это противоречит предположению (3.61). Теорема доказана.
Теорема 3.8. Пусть импульсная переходная функция q(t) и ее производные q(1)(t), q(2)(t),…,q(k)(t) являются оригиналами, а физически возможная квазирациональная дробь ( )=Q( )/D() есть изображение оригинала q(t), и пусть Q(0)0.
Тогда: 1) если один и только один корень квазимногочлена D() равен нулю и остальные его корни расположены на комплексной плоскости () слева от мнимой оси, то квазирациональная дробь () устойчивая, но не асимптотически;
67
2) если два или более корней квазимногочлена D() равны нулю и остальные его корни расположены на комплексной плоскости ( ) слева от мнимой оси, то квазирациональная дробь () неустойчива.
Доказательство. Пусть квазимногочлен D() имеет k нулевых корней, то есть =0 есть ноль k-го порядка
D() k D (), |
D (0) 0, k1 |
(3.62) |
k |
k |
|
Так как q(t), q(1)(t), q(2)(t),…, q(k)(t) являются оригиналами, а () есть изображение оригинала q(t), то справедлива формула изображения k-той производной
q(k ) (t)e t dt k ( ) q(0) k 1 q(1) (0) k 2 ... q(k 1) (0)
0
При 0 имеем
lim q(k )
0
0
(t)e t dt lim k ( ) q(k 1) (0)
0
В силу равномерной сходимости по интеграла в левой части данного равенства перейдем к пределу под знаком интеграла
q(k ) (t)dt lim k ( ) q(k 1) (0)
0
0
В силу аналитичности функции k() при Re >0 интеграл
левой части равенства (3.63) существует. Следовательно,
|
|
t |
|
|
|
|
|
|
|
|
|
q(k ) (t)dt lim |
q(k ) (t)dt limq(k 1) |
(t) q(k 1) (0) |
|||||||||
0 |
t |
|
t |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Из равенств (3.63), (3.64) с учетом (3.62) имеем |
|
|
|
||||||||
q(k 1) () lim q(k 1) (t) lim k () lim k |
|
Q() |
|
|
Q(0) |
, |
|||||
|
k |
Dk ( ) |
|
||||||||
|
t |
0 |
0 |
|
|
Dk (0) |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
0< Q(0) < , 0< Dk(0) < , k 1
(3.63)
q( k ) (t)dt в
0
(3.64)
(3.65)
Пусть квазимногочлен D() имеет только один нулевой корень, то есть k=1. Тогда
q() lim q(t) |
Q(0) |
const 0 |
(3.66) |
|
D1(0) |
||||
t |
|
|
||
|
|
|
Так как квазирациональная дробь ( ) имеет в точке =0 полюс и является изображением оригинала q(t), то существует такое M>0 и a>0, что
t 0 : |
|
q(t) |
|
Meat , |
a 0 |
(3.67) |
|
|
68

Следовательно, согласно (3.66), (3.67) и в соответствии с определениями 3.20 и 3.21 при k=1 квазирациональная дробь () является устойчивой, но не асимптотически.
Пусть k 2, то есть D() имеет два или более нулевых корней. Тогда согласно (3.65) при t установится постоянное значение (k-1)-ой
производной q(k 1) () Q(0) const 0 . Следовательно,
Dk (0)
q() |
|
lim |
|
q(t) |
|
lim |
|
Q(0) |
|
tk 1 |
|
... , |
k2 |
|
|
|
|
||||||||||
|
|
|
|
D (0) |
(k 1)! |
||||||||
|
|
t |
|
|
|
t |
|
|
|
|
|||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
и при k 2 |
|
квазирациональная дробь () является неустойчивой. Теорема |
|||||||||||
доказана. |
|
|
|
|
|
|
|
|
|
|
|
||
3.6. Параметрический синтез квазирациональных дробей
Если квазирациональная дробь асимптотически устойчива, то параметрический синтез этой дроби можно осуществить по ее вещественной частотной характеристике.
Пусть линейная стационарная комбинированная динамическая система задана асимптотически устойчивой физически возможной квазирациональ-
ной дробью
() Q() / D()
с импульсной переходной функцией (3.51)
|
2 |
|
|
|
q(t) |
ReФ(i ) costd , |
t0 , которая следует также из (3.53) при |
||
|
||||
|
0 |
|
0=0 и =i.
Положим, что на систему действует возмущение в виде единичной ступенчатой функции Хевисайда x(t) 1(t) .
Тогда реакцию системы называют переходной функцией и вычисляют по формуле
t |
2 |
|
sint |
|
|
h(t) q(t)dt |
ReФ(i ) |
d |
|||
|
|
||||
0 |
|
0 |
|
||
Определение 3.22. Переходной функцией h(t) физически возможной асимптотически устойчивой квазирациональной дроби ( )=Q( )/D() будем называть выражение
|
2 |
|
sin t |
|
|
|
h(t) |
Re (i ) |
d |
(3.68) |
|||
|
|
|||||
|
|
0 |
|
|
||
Выбираем желаемую вещественную частотную характеристику квазирациональной дроби в виде
69
Re * (i) |
|
1 2 2 |
|||
|
2 2 |
|
2 2 2 2 |
||
|
|||||
|
1 |
|
|||
которой соответствует согласно (3.68) желаемая переходная функция h*(t), имеющая экспоненциальный характер и время переходного процесса не более 3.
Пусть вещественная частотная характеристика Re Ф(i, T1, T2,…, Ts) зависит от параметров T1, T2,…, Ts с ограничениями Tj[aj , bj], j=1, 2,…, s. Введем в рассмотрение интеграл
|
Re (i ,T ,T ,...T ) Re * (i ) 2 d |
|
||
|
(3.69) |
|||
|
1 2 s |
|
|
|
0 |
|
|
|
|
Осуществляя многомерную минимизацию интеграла (3.69), выбираем значения параметров T1*, T2*,…, Ts*, при которых интеграл достигает минимума. Далее вычисляется переходная функция hс(t) прошедшей параметрический синтез физически возможной квазирациональной дроби
|
2 |
|
sin t |
|
|
|
hc (t) |
Re (i ,T1*,T2*,...Ts* ) |
d |
(3.70) |
|||
|
|
|||||
|
0 |
|
|
|||
и проводится анализ полученной переходной функции hс(t). При этом характеристический многочлен D*( , T1*, T2*,…, Ts*) прошедшей параметрический синтез квазирациональной дроби должен удовлетворять теореме 3.5, то есть должен быть устойчивым.
3.7. Динамическое моделирование упругого звена манипулятора
Ранее во второй главе была получена математическая модель (2.20) – (2.23) упругого звена манипулятора [9]. Если выражения (2.20) заменить выражениями (2.24), то получаем математическую модель упругого звена манипулятора с квазистатической моделью стержня. Если же функции
ij( ), i,j=1,2,3 из (2.20) заменить их |
пределами при 0, то есть принять |
|||||
|
lim () a(0) |
(0) , i,j=1,2,3, где |
a(0) |
– известны из (2.24), то получаем |
||
ij |
0 |
ij |
ij |
|
ij |
|
|
|
|
|
|
|
|
математическую модель упругого звена манипулятора с предельной квазистатической моделью стержня.
На первом этапе примем модель звена без груза на конце стержня m2=J2=0 с параметрами J0=7,1 10-3; k0=1,5 10-2; =4,8 10-3 ; p=31,5 и коррек-
тирующим устройством
70
