Лекции №26-27 Векторное (линейное) пространство над полем к

Определение. Линейным пространством над числовым полем К называется множество R элементов, которые будем называть векторами и обозначать ,,и так далее, если:

1. Указан закон, согласно которому любой паре векторов ,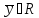однозначно ставится в соответствие вектор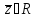, называемый суммой векторов().

2. Указан закон, согласно которому каждому числу из поляК при однозначно ставится в соответствие вектор. Вектор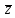называется произведениеми обозначается( или).

3. Введенные в п.1 и п.2 операции сложения векторов и умножения вектора на число удовлетворяют следующим аксиомам:

• ,

• ,

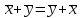• Существует элемент такой, что,

• . Вектор называется противоположным вектору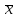и обозначается «»,

• , ,

• 

• ,

• =

Из этих аксиом следует, что :

1. В линейном пространстве существует единственный нулевой вектор.

2. В линейном пространстве каждый вектор имеет единственный противоположный вектор.

3. справедливо равенство

Линейные оболочки

Определение. Линейной оболочкой семейства векторов называется множество их всевозможных линейных комбинаций в линейном пространстве L.

Легко проверить, что линейная оболочка является линейным пространством в L.

Линейную оболочку также называют подпространством, натянутым на векторыили порожденным векторами семействаЕе можно определить еще как пересечение всех подпространств вL, содержащих все Рангом семейства векторов называется размерность его линейной оболочки.

Первое характеристическое свойство базиса: его линейная оболочка совпадает со всем L.

Подпространства

Определение. Линейное подпространство или векторное подпространство – это непустое множество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространство обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

1. ,

2. для всякого вектора , вектортакже принадлежалK, при любом ,

3. для векторов , вектортакже принадлежалK.

Последние два утверждения эквивалентны следующему :

• для всяких векторов , вектортакже принадлежалK для любых

В частности, пространство, состоящее из одного элемента является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называютсобственными или нетривиальными.

Свойства подпространств

1. Пересечение любого семейства подпространств – снова подпространство;

2. Сумма конечного семейства подпространств – снова подпространство.

3. Сумма подпространств определяется как множество, содержащее всевозможные суммы элементов:

В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.

Линейная зависимость векторов

Определение. Семейство векторов называется линейнонезависимым, если никакая нетривиальная линейная комбинация не равна нулю, то есть из

следует, что все 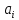= 0. В противном случае оно называется линейнозависимым. Линейная независимость семейства означает, чтонулевой вектор однозначно представляется в виде линейной комбинации элементов семейства. Тогда любой другой вектор имеет либо единственной представление, либо ни одного. Действительно, сравнивая два представления

Отсюда следует второе характеристическое свойство базиса: его элементы линейно независимы. Определение этих двух свойств равносильно первоначальному определению базиса.

Заметим, что семейство векторов линейно независимо тогда и только тогда, когда оно образует базис своей линейной оболочки.

Семейство заведомо линейно зависимо, если среди векторовесть нулевой или два одинаковых.

Лемма 1. Семейство векторов линейно зависимо тогда и только тогда, когда хотя бы один из векторовявляется линейной комбинацией остальных.

Доказательство.

Если и

Наоборот, если , то

Лемма 2. 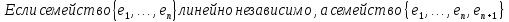линейно зависимо, то является линейной комбинацией.

Доказательство.

Если 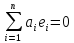не всеравны, то обязательно, иначе мы получили бы нетривиальную зависимость междуПоэтому

Лемма доказана.