Лекции 7-8 Системы линейных алгебраических уравнений

Cистема имеет вид:

(1)

Коэффициенты при неизвестных составляют матрицы

Решением системы линейных уравнений (1) называется такая система п чисел , что каждое из уравнений (1) обра­щается в тождество после замены в нем неизвестных соответ­ствующими числами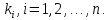

Система линейных уравнений может не иметь ни одного реше­ния и тогда она называется несовместной. Такова, например, си­стема

Если же система линейных уравнений обладает решениями, то она называется совместной. Совместная система называется опре­деленной , если она обладает одним-единственным решением — лишь такие системы допускаются к рассмотрению в элементарной алгебре,— и неопределенной, если решений больше чем одно; как мы узнаем позже, их будет в этом случае даже бесконечно много. Так, система

определенна: она имеет решение и, как легко про­веряется методом исключения неизвестного, это решение будет един­ственным. С другой стороны, система

неопределенна, так как имеет бесконечно много решений вида

(2)

где число k произвольно, причем решениями, получающимися по формулам (2), исчерпываются все решения нашей системы.

Задача теории систем линейных уравнений состоит в разработке методов, позволяющих узнать, совместна ли данная система уравне­ний или нет, в случае совместности установить число решений, а также указать способ найти все эти решения.

Рассмотрим систему линейных уравнений (1).

Как мы знаем, прежде всего следует решить вопрос о сов­местности этой системы. Для этой цели возьмем матрицу A из коэф­фициентов системы и «расширенную» матрицу , полученную при­соединением к А столбца из свободных членов,

A =,=,

и вычислим ранги этих матриц. Легко видеть, что ранг матрицы либо равен рангу матрицы А, либо на единицу больше последнего.В самом деле, берем некоторую максимальную линейно независимую систему столбцов матрицы А. Она будет линейно независимой и в ма­трице .Если она сохраняет и свойство максимальности, т. е. столбец из свободных членов через нее линейно выражается, то ранги матрицыА и равны; в противоположном случае, присоединяя к этой системе столбец из свободных членов, мы получаем линейно неза­висимую систему столбцов матрицы, которая будет в ней макси­мальной.

Вопрос о совместности системы линейных уравнений полностью решается следующей теоремой.

Теорема Кронекера — Капелли.

Система линейных урав­нений (1) тогда и только тогда совместна, когда ранг расши­ренной матрицы равен рангу матрицыА.

Рассмотрим основные способы решения Решение систем линейных алгебраических уравнений.

1. Решение систем линейных алгебраических уравнений по правилу Крамера.

Пусть дана система n-линейных алгебраических уравнений с n неизвестными:

Запишем главный определитель системы:

∆ = .

Выпишем вспомогательные определители, заменяя 1, 2, n-ый столбец столбцом из свободных членов:

∆.

∆= .

∆= .

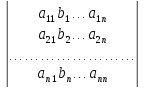Правило Крамера:

Если главный определитель системы отличен от нуля, то система имеет решение, это решение единственное и находится по формулам:

= ,=,=.

Пример.

Решить систему линейных алгебраических уравнений по правилу Крамера:

Решение:

Составим главный определитель системы:

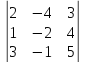∆ = = – 20 – 48 – 3 + 18 + 8 + 20 = – 25.

Выпишем вспомогательные определители:

∆x = = – 10 – 32 – 9 + 12 + 4 + 60 = 25.

∆y = = 30 + 12 + 6 – 27 – 16 – 5 = 0.

∆z = = – 8 – 36 – 1 + 6 + 6 + 8 = – 25.

Используя формулы, приведенные выше, найдем решение данной системы:

x =