
- •II.Элементы функционального и комплексного анализа.
- •Решение задачи:
- •6. Формула включений и исключений.
- •Упражнения и задачи по теории множеств
- •III. Введение в математический анализ. Дифференциальное исчисление функции.
- •Тема 1. Введение в математический анализ. Область определения функции совпадает с одз (областью допустимых значений) правой части, т.Е. С множеством всех значений х, при которыхвычисляется.
- •Вопросы для самопроверки:
- •Тема 2. Пределы
- •Вопросы для самопроверки:
- •Тема 3. Дифференциальное исчисление
- •Вопросы для самопроверки:
- •Тема 4. Приложения дифференциального исчисления
- •Вопросы для самопроверки:
- •Тема 5. Функции нескольких переменных
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •IV. Интегральное исчисление функции одной переменной.
- •Тема 1. Неопределенный интеграл
- •Вопросы для самопроверки.
- •Тема 6. Определенный интеграл
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •V. Дифференциальные уравнения.
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •VI. Числовые и функциональные ряды. Числовые ряды
- •Функциональные ряды
- •VII. Элементы теории вероятностей. Случайные события
- •Вопросы для самопроверки:
Вопросы для самопроверки:
В чем заключается правило Лопиталя?
Каковы признаки возрастания и убывания функции?
Сформулируйте достаточные условия экстремума функции.
Как находятся интервалы выпуклости и вогнутости и точки перегиба кривой
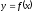 ?
?
Тема 5. Функции нескольких переменных
Основная проблема при изучении этой темы возникает в момент дифференцирования указанных функций. Это связано с тем, что при дифференцировании функции по одной переменной все другие переменные предполагаются постоянными величинами. Например,
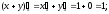
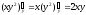

Задача
1.
Найти частные производные функции
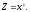
Решение:
Найдем производную функции Z
по переменной x.
В этом случае, при дифференцировании
величина y
считается постоянной и поэтому:
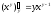
Аналогично
найдем производную функции по y,
считая величину x
постоянной:
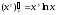
Вопросы для самопроверки:
Что называется функцией двух переменных?
Дайте определения частных производных.
Как находится экстремум функции нескольких переменных?
В чем состоит способ наименьших квадратов построения эмпирических формул?
Задачи для самоконтроля
Задание 1. Вычисление пределов
1.а)
 ;
б)
;
б)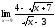 ;
;
в)
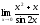 ;
г)
;
г)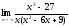 .
.
2.
а)
 ;
б)
;
б)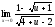 ;
;
в)
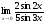 ;
г)
;
г)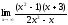 .
.
3.
а)
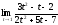 ;
б)
;
б)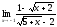 ;
;
в)
 ;
г)
;
г)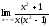 .
.
4.
а)
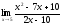 ;
б)
;
б) ;
;
в)
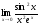 ;
г)
;
г)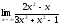 .
.
5.
а)
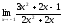 ;
б)
;
б)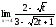 ;
;
в)
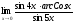 ;
г)
;
г)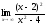 .
.
6.
а)
 ;
б)
;
б)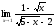 ;
;
в)
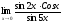 ;
г)
;
г)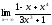 .
.
7.
а)
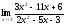 ;
б)
;
б)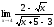 ;
;
в)
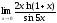 ;
г)
;
г)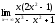 .
.
8.
а)
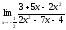 ;
б)
;
б)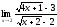 ;
;
в)
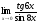 ;
г)
;
г) .
.
9.
а)
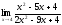 ;
б)
;
б)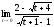 ;
;
в)
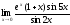 ;
г)
;
г)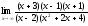 .
.
10.
а)
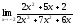 ;
б)
;
б)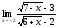 ;
;
в)
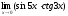 ;
г)
;
г) .
.
Задание 2. Дифференциальное исчисление
Найти производную и дифференциал функций:
11.
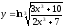 ;
16.
;
16. ;
;
12.
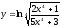 ;
17.
;
17.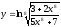 ;
;
13.
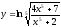 ;
18.
;
18.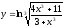 ;
;
14.
 ;
19.
;
19.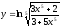 ;
;
15.
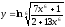 ;
20.
;
20.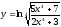 .
.
Найти
производную

21.
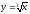 ;
26.
;
26. ;
;
22.
 ;
27.
;
27. ;
;
23.
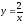 ;
28.
;
28.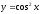 ;
;
24.
 ;
29.
;
29.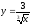 ;
;
25.
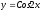 ;
30.
;
30.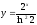 .
.
Найти пределы функций с помощью правила Лопиталя:
31.
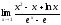 ;
36.
;
36.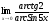 ;
;
32.
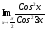 ;
37.
;
37.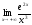 ;
;
33.
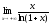 ;
38.
;
38.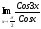 ;
;
34.
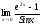 ;
39.
;
39.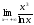 ;
;
35.
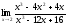 ;
40.
;
40.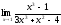 .
.
Исследовать функцию и построить график :
41.
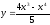 ;
46.
;
46. ;
;
42.
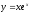 ;
47.
;
47.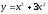 ;
;
43.
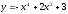 ;
48.
;
48.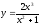 ;
;
44.
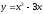 ;
49.
;
49.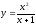 ;
;
45.
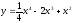 ;
50.
;
50.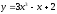 .
.
Задание 4. Функции нескольких переменных.
Найти частные производные функции Z = Z(x,y)
61. Z = 2x3-3xy2+y5;
62. Z = x4+2x2-xy3 ;
63. Z = 5x-2x3y2+2y4;
64. Z = -x2+5xy5-2y3x;
65. Z = x3-3x2y+xy2-y3;
66. Z = 4x-7x4y+3y5;
67. Z = x4+2x2y2+y4;
68. Z = x3+3x2y+3xy2+y3;
69. Z = 6x3-5x2y3+x3y2;
70. Z = x6+2x3y2+y4.
Найти экстремумы функций:
71. Z = x3+8y3+6xy+5;
72. Z = x2+xy+y2-3x-6y;
73. Z = x2+y2+8x-2;
74. Z = y2+yx+x2-6y-9x;
75. Z = x2-xy+y2+9x-6y+20;
76. Z = 3x2-y2+4y+5;
77. Z = x2-4x+y2;
78. Z = x2+xy+2y2-x+y;
79. Z = 3x2-6x-y2+4y+8;
80. Z = x2+xy+x+2y2+2y.
IV. Интегральное исчисление функции одной переменной.
Тема 1. Неопределенный интеграл
[1, гл IX, § 9.1 – 9.3],[4, гл VII]
Эффективным способом интегрирования функций является замена переменной. Его целью является получение с помощью новой переменной более простого интеграла.
Задача
1.
Найти
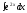
Решение:
Сделаем замену 2x=t. Для нахождения dx через t продифференцируем обе части уравнения:
 .
Теперь
.
Теперь

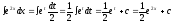 .
.
Задача
2.
Найти
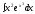 .
.
Решение: 1-й способ. Сделаем замену
э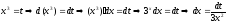
Очевидно,
выразить dx
только через t
рациональным способом не удается.
Однако после подстановки полученных
выражений для
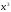 иdx
через t
исходный интеграл принимает вид:
иdx
через t
исходный интеграл принимает вид:
 .
Можно было поступить по-другому. Нетрудно
видеть, что в равенстве
.
Можно было поступить по-другому. Нетрудно
видеть, что в равенстве
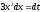 левая часть содержит часть подынтегрального
выражения, а именно
левая часть содержит часть подынтегрального
выражения, а именно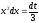 .
Поэтому
.
Поэтому и т.д.
и т.д.
2-й способ. Сделаем другую замену:
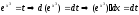
 и
подынтегральное выражение сразу очень
просто выражается через t:
и
подынтегральное выражение сразу очень
просто выражается через t:
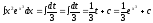 .
.
