
КомпГр_ЛР1_Заболотников_Петрова_Романова_9373
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра Информационных систем
ОТЧЁТ по лабораторной работе №1
по дисциплине «Компьютерная графика» Тема: Исследование математических методов представления и
преобразования графических объектов на плоскости и в пространстве.
Студент гр. 9373 |
_______________ |
Заболотников М. Е. |
Студентка гр. 9373 |
_______________ |
Петрова С. В. |
Студентка гр. 9373 |
_______________ |
Романова Е. С. |
Преподаватель |
_______________ |
Матвеева И.В. |
Санкт-Петербург
2022
Цель работы.
Сформировать отрезок, касательный к двум заданным окружностям с внешней стороны, определив предварительно координаты точек касания.
Необходимо предусмотреть возможность редактирования положения и параметры окружностей.
Задание на работу.
Необходимо написать программу, которая рисует отрезок, касательный к двум заданным окружностям с внешней стороны.
Общие сведения.
Для выполнения данной работы будут использоваться следующие
теоретические сведения.
Пусть даны две точки 1 и 2 в декартовой системе координат, которые
имеют координаты ( 1, 1) и ( 2, 2), |
и необходимо вычислить расстояние |
|||||
между ними. Данное расстояние находится по следующей формуле: |
|
|||||
|
|
|
|
|
|
|
= √( |
− |
)2 + ( |
− )2 |
(1) |
||
2 |
1 |
2 |
1 |
|
|
|
Пусть даны две точки 1 и 2 в декартовой системе координат, которые имеют координаты ( 1, 1) и ( 2, 2) и через которые требуется провести прямую. В этом случае уравнение такой прямой – через координаты данных точек – будет иметь вид:
|
|
− 1 |
= |
− 1 |
|
(2) |
|||
|
|
|
|
− |
|||||
|
|
|
− |
|
|||||
2 |
1 |
|
2 |
1 |
|
|
|
||
Если провести алгебраические преобразования, то можно представить |
|||||||||
данное уравнение в следующем виде: |
|
|
|
|
|
||||
= |
(2 − 1) + 2 1 − 1 2 |
, |
(3) |
||||||
|
|||||||||
|
|
|
2 − 1 |
|
|||||
или |
|
|
|
|
|
|
|
||
|
|
|
= + , |
(4) |
|||||
|
|
|
2 |
|
|
|
|
|
|
где = |
2− 1 |
– тангенс угла наклона прямой, а = |
2 1− 1 2 |
– свободный |
|||
− |
1 |
− |
1 |
||||
|
|
|
|||||
|
2 |
|
2 |
|
|||
коэффициент.
Далее рассмотрим процесс "поворота" прямой относительно некоторой точки, лежащей на этой прямой. Пусть имеются всё те же две точки 1 и 2,
которые лежат на нашей прямой, и мы хотим "повернуть" прямую вокруг точки 1 на некоторый угол . Данную задачу можно рассматривать как задачу поворота какой-либо другой точки прямой вокруг точки 1. Поэтому мы можем взять в качестве такой точки нашу точку 2. В таком случае её новые координаты ( , ) будут выражаться следующим образом:
|
|
|
|
cos( ) |
−sin( ) |
2 |
− 1 |
1 |
(5) |
|
|
|
( ) = (sin( ) |
cos( ) ) ( 2 |
− 1) + |
( 1) |
|||
Далее по формуле (1) мы получим новую прямую, проходящую через |
|||||||||
точки |
( |
, |
) и ′ ( , ). |
|
|
|
|
|
|
1 |
1 |
1 |
2 |
|
|
|
|
|
|
И в конце рассмотрим механизм параллельного переноса прямой на |
|||||||||
заданное расстояние . |
Пусть |
у нас имеется прямая = + , |
которую |
||||||
необходимо перенести. Тогда уравнение новой прямой, параллельной данной,
выраженное через уравнение старой, будет иметь вид: |
|
||
= + ± |
|
, |
(6) |
|
|||
cos( ) |
|||
где – угол наклона прямой, тангенс которого равен .
3
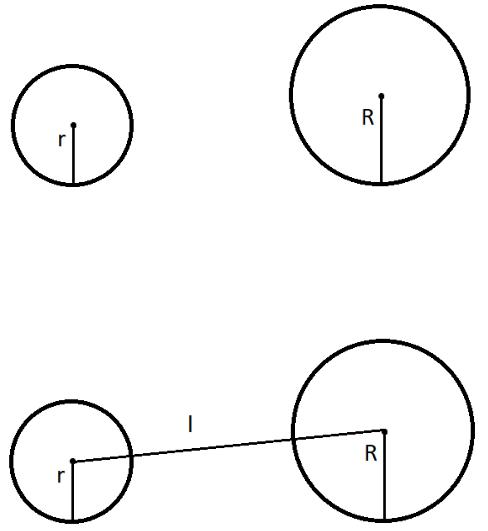
Ход работы.
Рассмотрим две окружности, расположенные в координатной плоскости произвольным образом (см. рис. 1).
Рисунок 1 – Две окружности Для простоты рассуждений будем полагать, что малая из двух
окружностей имеет радиус , а большая – радиус ( > ). Первым делом, по формуле (1), найдем расстояние между центрами окружностей (см. рис. 2).
Рисунок 2 – Расстояние Здесь 1 и 1 – это координаты центра малой окружности, а 2 и 2
– координаты центра большей окружности.
Далее изобразим касательную к двум окружностям. Будем работать с уравнениями исследуемых прямых. Теперь необходимо "повернуть" нашу прямую на угол так, чтобы она стала параллельна нашей будущей касательной (см. рис. 3).
4
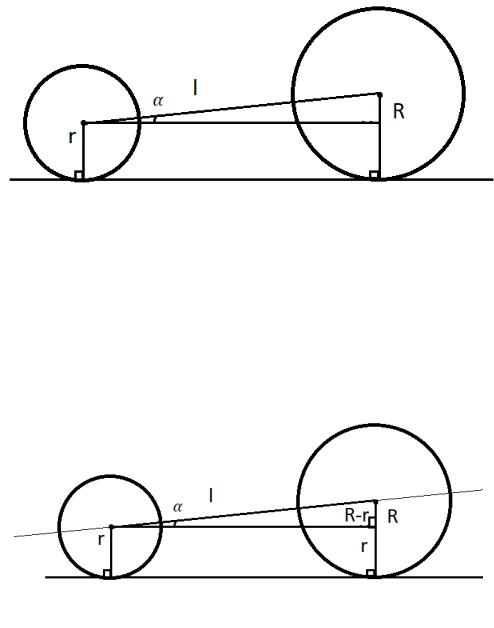
Рисунок 3 – Касательная к двум окружностям Для выполнения поворота прямой с последующим нахождением её
уравнения рассмотрим задачу о повороте центра большей окружности вокруг
центра малой на угол . Тогда новые координаты данной точки ′ |
|
( , ) |
|||||
|
|
|
|
|
|||
|
− |
|
|
|
|
||
найдутся по формуле (5), где sin( ) = |
, а cos( ) = √1 − (sin( ))2 |
(см. рис. |
|||||
|
|||||||
|
|
|
|
||||
4). |
|
|
|
|
|
|
|
Рисунок 4 – Поворот прямой
Теперь, зная две точки |
и ′ |
, можно построить уравнение прямой |
|
|
|
, по формуле (2), и привести его к виду (формула (4)). Так как прямая параллельна касательной (прямой ), то их углы наклона равны. Далее осуществляется перенос прямой до прямой на расстояние радиуса малой окружности (см. рис. 5). Такой подход имеет место быть, потому что мы знаем,
что касательная перпендикулярна радиусу, проведённому в точку касания.
5
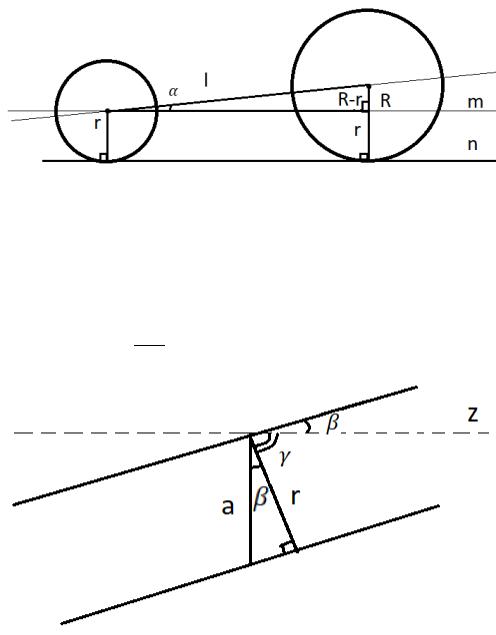
Рисунок 5 – Параллельные прямые Теперь, имея уравнение прямой , по формуле (6), построим уравнение
нашей касательной . Угол – это угол наклона прямой, причём = arctg( ).
Расстояние для переноса параллельной прямой будет расчитываться следующим способом: = .
Рисунок 6 – Расстояние между параллельными прямыми (здесь –
некоторая прямая, параллельная оси абсцисс)
Итак, уравнение прямой : = + . Таким образом, уравнение для касательной будет иметь вид: = + 1, где 1 = ± . Знак зависит оттого, поднимаем мы прямую или нет.
Есть случаи, когда касательная параллельна оси ординат и не находится, так как (90°) не определён (см. рис. 5), тогда уравнение прямой для касательной будет иметь вид: = . В этом случае касательная будет строиться иначе.
6
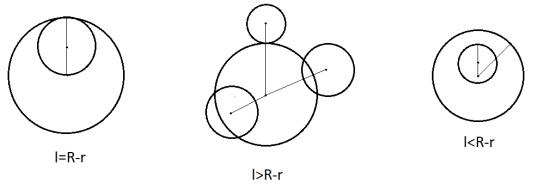
Рассмотрим работу программы.
В начале программа найдет расстояние между центрами и проверит,
существует ли между двумя окружностями касательная (см. рис. 7).
Рисунок 7 – Варианты расположения окружностей Из рис. 7 понятно, если расположение окружностей друг относительно
друга таково, что < − , то в этом случае малая окружность лежит внутри большей. Такие окружности не имеют общей касательной. В случае, когда =− , окружности касаются внутренним образом, что означает, что точка касания прямой для этих окружностей – общая для них обеих.
Если касательной нет, то программа не будет проводить дальнейшие вычисления, а если есть, то будет проверять условия ( 2,
1, 2, 1, , ):
1. Если |
+ |
|
= |
+ |
и |
> |
|
, |
то |
прямая |
будет |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
строиться |
по |
точкам: |
|
= ( |
|
+ |
|
, |
|
+ |
|
) и |
= |
||
|
|
|
|
1 |
|
|
|
|
|
|
2 |
||||
( + , + ).
2.Если − = − и < , то прямая будет строиться по точкам: 1 = ( − , − ) и 2 = ( −
, + ).
Если ни одно из первых двух условий не выполняется, то рассматриваются другие. Для нижеописанных условий уже известен угол поворота , был совершен поворот центра большой окружности относительно малой, найдено уравнение прямой : = + , также найдено расстояние
, на которое необходимо подвинуть эту прямую. Рассмотрим эти условия:
7
3.Если + > + и > , или − >− и = , или − > − и <
– тогда 1 для уравнения прямой касательной будет рассчитываться так: 1 = − .
4.Если − < − и < , или + <
|
+ |
|
и |
= |
, или |
+ |
< |
|
+ |
и |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
– |
тогда |
|
для |
уравнения прямой |
касательной |
будет |
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
рассчитываться так: 1 = + .
Выполнение работы.
Ссылка на видео с демонстрацией работы программы:
https://youtu.be/8e53HewyKmw
Программа была написана в приложении Qt на языке C++ с
использованием графических библиотек. Полный код программы представлен в приложении А.
Для работы с программой необходимо ввести координаты центров окружностей и радиусы, а затем нажать на кнопки «Обновить» и «Построить прямую».
8
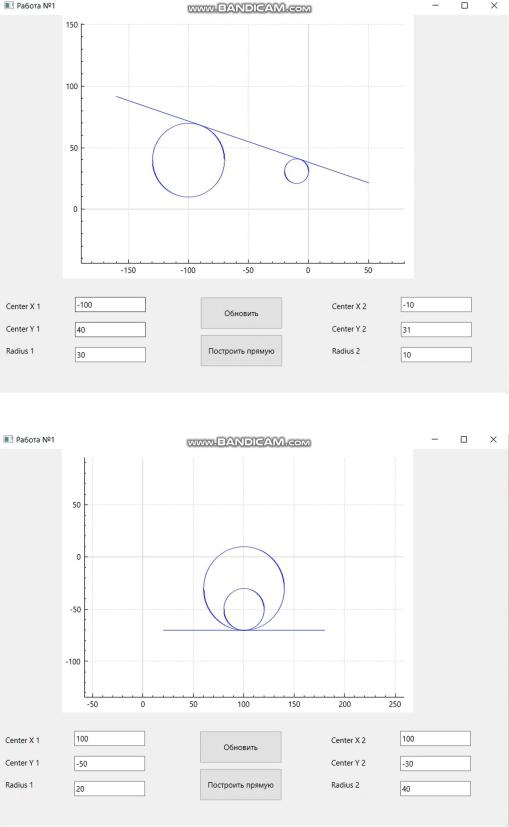
Тесты работы программы.
На рис. 8 – 11 представлены результаты выполнения работы программы:
Рисунок 8 – Касательная к окружностям под наклоном
Рисунок 9 – Окружности касаются внутренним образом
9
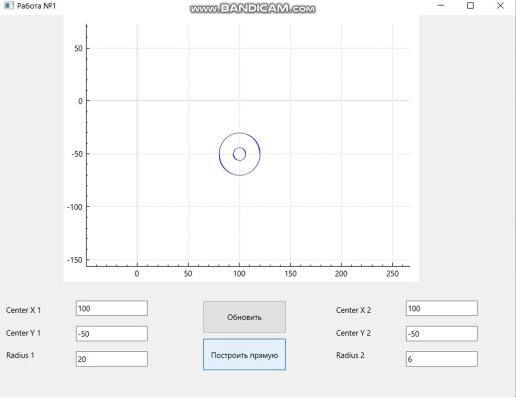
Рисунок 10 – Отсутствие касательной
10
