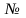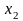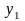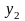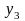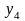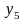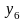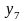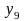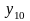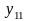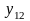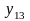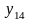- •Основы компьютерной арифметики и логики
- •Предисловие
- •Глава 4, подготовленная доцентом о.П. Шафеевой, посвящена вопросам разработки алгоритмических моделей выполнения арифметических операций и моделирования на пэвм спроектированных алгоритмов.
- •Основы двоичной компьютерной арифметики
- •1.1. Позиционные системы счисления
- •Десятичная позиционная система счисления
- •Двоичная позиционная система счисления
- •1.1.3. Восьмеричная позиционная система счисления
- •1.1.4. Шестнадцатеричная позиционная система счисления
- •Сложение Вычитание
- •Перевод чисел из одной позиционной системы счисления в другую
- •1.2.1. Перевод целых чисел
- •1.2.2. Перевод правильных дробей
- •1.2.3. Перевод неправильных дробей из одной системы счисления в другую
- •1.2.4. Частный случай перевода чисел из одной системы счисления в другую
- •1.2.5. Перевод чисел из одной системы счисления в другую с использованием промежуточной двоично-десятичной системы
- •1.3. Представление чисел с фиксированной запятой (точкой)
- •1.4. Представление чисел с плавающей запятой (точкой)
- •1.5. Коды двоичных чисел
- •1.5.1. Прямой код
- •1.5.2. Обратный код
- •1.5.3. Модифицированный обратный код
- •1.5.4. Дополнительный код
- •2.1.1. Алгебраическое сложение чисел в дополнительном коде
- •2.1.2. Алгебраическое сложение чисел в обратном коде
- •2.1.3. Переполнение разрядной сетки при сложении чисел
- •2.2. Сложение (вычитание) двоичных чисел с плавающей запятой
- •2.2.1. Метод ускоренного сложения двоичных чисел с запоминанием переносов
- •2.3. Умножение двоичных чисел с фиксированной запятой
- •2.4. Машинные технологии выполнения операции умножения двоичных чисел с фиксированной запятой
- •2.5. Умножение двоичных чисел с плавающей запятой
- •2.6. Методы ускоренного выполнения операции умножения двоичных чисел
- •2.6.1. Метод пропуска такта суммирования
- •2.6.2. Метод анализа сомножителей
- •2.6.3. Метод расшифровки и одновременного умножения на два разряда множителя
- •2.6.4. Метод ускоренного умножения Мак-Сорли
- •2.6.5. Метод ускоренного умножения Лемана
- •2.6.6. Метод умножения с расшифровкой пар разрядов множителя и запоминанием переносов
- •2.7. Деление двоичных чисел с фиксированной запятой
- •2.8. Деление двоичных чисел с плавающей запятой
- •3. Основы десятичной компьютерной арифметики
- •3.1. Машинное кодирование десятичных чисел
- •3.2. Выполнение арифметических операций с десятичными числами
- •3.2.1. Сложение десятичных чисел в эвм
- •3.2.2. Умножение десятичных чисел в эвм
- •3.2.3. Ускорение умножения в -кодах
- •Деление десятичных чисел в эвм
- •4.2. Моделирование алгоритма сложения двоичных чисел
- •Различные случаи ненормализованных мантисс
- •4.3. Проектирование алгоритма умножения чисел
- •4.5. Проектирование алгоритма деления чисел
- •4.7. Разработка алгоритма вычисления квадратного корня
- •Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств
- •Свойства отношений
- •Эквивалентность
- •Толерантность
- •Отношения порядка
- •Самодвойственные функции
- •Монотонные функции
- •Линейные функции
- •Функции, сохраняющие константу
- •5.2.7. Минимизация булевых функций
- •Метод Блейка
- •Метод Квайна-Мак-Класки
- •Минимизация с использованием карт Карно
- •Дана функция четырех переменных (рис. 5.13):
- •Минимизация не полностью определенных булевых функций
- •Минимизация систем булевых функций
- •5.3. Методика синтеза комбинационных схем на логических элементах
- •5.3.1. Логические элементы
- •5.3.2. Общий алгоритм построения комбинационных схем
- •5.3.3. Синтез кс в классическом базисе
- •5.3.4. Синтез кс в базисах «и-не», «или-не»
- •5.3.5. Реализация кс в базисе Жегалкина
- •5.3.6. Синтез составных кс
- •Заключение
- •Библиографический список к главам 1, 2, 3, 4
- •Библиографический список к главе 5
Отношения порядка
Определение 18. Строгим порядком называют отношения, которые одновременно антирефлексивны и транзитивны, т.е.
(
строгий
порядок )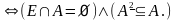
Например,
отношение «меньше» антирефлексивно,
т.к. условие
не выполняется ни при каком значении
,
и транзитивно (условие
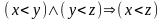 выполняется при любых значениях
выполняется при любых значениях
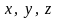 ),
следовательно, это строгий порядок.
Другие примеры отношений строгого
порядка: «больше», «старше», «сильнее»,
«правее», «ниже», «быть предком», «быть
потомком» и т.д.
),
следовательно, это строгий порядок.
Другие примеры отношений строгого
порядка: «больше», «старше», «сильнее»,
«правее», «ниже», «быть предком», «быть
потомком» и т.д.
Отношение «быть меньше ровно на единицу» строгим порядком не является, т.к. оно не транзитивно, но его транзитивное замыкание (отношение «меньше») есть строгий порядок.
Теорема 8. Отношение строгого порядка асимметрично, т.е.
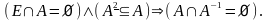
Доказательство.
Предположим противное. Пусть
.
Тогда существует пара

 .
Откуда
и
или
.
Откуда
и
или
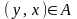 ,
т.е. выполняется условие
,
т.е. выполняется условие
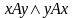 ,
из которого на основании свойства
транзитивности следует выполнение
условия
,
из которого на основании свойства
транзитивности следует выполнение
условия
 ,
т.е.
,
т.е.
 ,
но это противоречит свойству
антирефлексивности отношения
.
Данное противоречие и доказывает, что
.
Теорема доказана.
,
но это противоречит свойству
антирефлексивности отношения
.
Данное противоречие и доказывает, что
.
Теорема доказана.
Определение 19. Нестрогим порядком называют отношения, которые одновременно рефлексивны, антисимметричны и транзитивны, т.е.
нестрогий
порядок
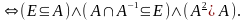
Примеры
отношений нестрогого порядка: «меньше
либо равно» (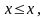
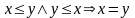 ,
,
 для любых
),
«не меньше», «не выше», «не хуже», «быть
подмножеством» (
для любых
),
«не меньше», «не выше», «не хуже», «быть
подмножеством» (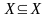 ,
,
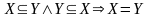 ,
,
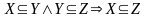 для любых множеств
для любых множеств
 ).
).
Множество
,
на котором задано отношение
порядка (строгого или нестрогого),
называется полностью
упорядоченным,
если для любых отличных друг от друга
элементов
и
этого множества будет выполняться либо
условие
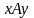 ,
либо условие
,
либо условие
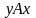 .
.
Примерами полностью упорядоченных множеств являются все числовые множества, т.к. любые два различных числа можно сравнить и определить наибольшее (наименьшее).
Определение
20.
Множество
называется частично
упорядоченным,
если на нем задано отношение
порядка (строгого или нестрогого), но
не для любых его элементов
и
выполняется условие
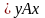 ,
а само это отношение называется частичным
(строгим или нестрогим) порядком.
,
а само это отношение называется частичным
(строгим или нестрогим) порядком.
Например,
отношение «быть подмножеством», является
частичным нестрогим порядком, а
совокупность множеств, на которой он
задан, будет частично упорядоченным
множеством. В этой совокупности не любые
множества сравнимы между собой. В
частности, отрезок
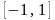 действительной оси не сравним с отрезком
действительной оси не сравним с отрезком
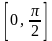 (отрезок
не является подмножеством отрезка
,
а
(отрезок
не является подмножеством отрезка
,
а
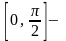 подмножеством
,
что означает их несравнимость).
подмножеством
,
что означает их несравнимость).
Примером частичного порядка является также отношение «подчиненности», определенное на множестве сотрудников некоторого учреждения (директору подчиняется начальник отдела, но начальники разных отделов друг другу не подчиняются).
Отношения порядка (а к ним относится еще и не рассмотренный здесь древесный порядок [7]) не менее эквивалентности важны в научных исследованиях. Все наши знания, да и вся человеческая деятельность, по крайней мере частично упорядочены. Такова природа процесса познания реального мира. Процесс познания мира математики задается отношением «определяться через более широкое понятие». В частности, изложение материала в настоящем пособии идет в соответствии с тем порядком, который задается данным отношением. Отталкиваясь от понятия абстрактного множества, мы дали четкие математические определения подмножеству, разбиению, соответствию, логической функции, отношению и многим другим математическим объектам (эйдосам). Такая последовательность изложения продиктована самой природой мира математики, который, как теперь выяснилось, является упорядоченным множеством математических понятий.
Вопросы для самоконтроля
Докажите, что противоположным отношению строгого порядка будет нестрогий порядок.
На множестве всех определенных выше математических объектов задано отношение «определяется через». Задайте данное отношение в виде графа.
5.2. Булевы функции
Особое место в математике занимают логические функции, аргументами которых являются двузначные логические переменные, т.е. в самом общем виде эти функции суть однозначное соответствие вида
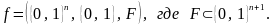 (5.18)
(5.18)
Здесь
число независимых переменных, от которых
зависит функция
 (
=1,
2, …);
(
=1,
2, …);
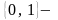 область изменения этих переменных
(такие переменные называют булевыми),
а также и область значений
-арной
булевой
функции
область изменения этих переменных
(такие переменные называют булевыми),
а также и область значений
-арной
булевой
функции
 ,
график которой определяется множеством
,
представляющим собой
-мерную
«гиперкривую» в гиперплоскости
,
график которой определяется множеством
,
представляющим собой
-мерную
«гиперкривую» в гиперплоскости
 .
.
В технике существует эквивалентное название – переключательные функции (ПФ). Данное название указывает на то, что переключательные функции реализуются схемами с использованием вентильных элементов (т.е. логических элементов, представляющие собой схемы переключения электрических сигналов).
Обратим
внимание, что областью отправления
соответствия (5.18) является единичный
-мерный
гиперкуб. Гиперкуб
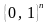 - это множество из
- это множество из
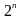 элементов, а булеан гиперкуба (множество
всех его подмножеств) будет содержать
уже
элементов, а булеан гиперкуба (множество
всех его подмножеств) будет содержать
уже
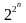 элементов.
Согласно (5.18) любая булева функция
определяет разбиение гиперкуба на две
области (истинности и ложности). Поэтому
число различных функций
равно
элементов.
Согласно (5.18) любая булева функция
определяет разбиение гиперкуба на две
области (истинности и ложности). Поэтому
число различных функций
равно
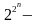 числу различных подмножеств гиперкуба
.
числу различных подмножеств гиперкуба
.
Поскольку
области значений таких функций и их
переменных полностью совпадают, то это
дает возможность в качестве аргумента
булевой функции использовать булеву
функцию и тем самым получить новую
булеву функцию. Иначе говоря, на множестве
булевых функций задана операция
композиции
 ,
позволяющая из функций
,
позволяющая из функций
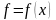 и
и
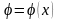 сконструировать еще одну булеву функцию
сконструировать еще одну булеву функцию
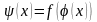 .
.
Следовательно, на множестве булевых функций можно найти минимальный набор самых простейших (изначальных) функций, из которых, с помощью применения операции композиции произвольное число раз, можно будет получить все остальные булевы функции. Видимо и в мире булевых функций существует неравнозначность, удерживаемая некоторым порядком, который нам предстоит открыть. Этим и займемся.
5.2.1. Логические операции соединения
Сначала
рассмотрим множество бинарных
булевых функций, т.е. функций
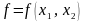 двух (
двух (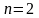 )
булевых переменных
и
)
булевых переменных
и
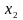 .
Бинарные булевы функции еще называют
логическими
операциями соединения.
Их общее число равно
.
Бинарные булевы функции еще называют
логическими
операциями соединения.
Их общее число равно
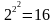 .
Столько подмножеств имеет единичный
квадрат
.
Столько подмножеств имеет единичный
квадрат
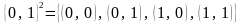 ,
изображенный на рис.
5.7 и 5.8.
,
изображенный на рис.
5.7 и 5.8.
Полный перечень бинарных булевых функций представлен в табл. 5.1.
В
данной таблице в крайнем левом столбце
указаны булевы переменные (
и
)
и функции (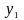 ,
,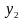 ,
…,
,
…,
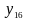 )
как обозначение соответствующих строк
таблицы. В последующих четырех столбцах
указаны области истинности соответствующих
функций. В первой строке этих столбцов
указаны номера вершин единичного
квадрата (рис. 5.7), а во второй и третьей
строках – координаты этих вершин (первая
и вторая компоненты соответственно).
)
как обозначение соответствующих строк
таблицы. В последующих четырех столбцах
указаны области истинности соответствующих
функций. В первой строке этих столбцов
указаны номера вершин единичного
квадрата (рис. 5.7), а во второй и третьей
строках – координаты этих вершин (первая
и вторая компоненты соответственно).
В
строках, помеченных символами
,
,
…,
,
в области этих столбцов стоят нули и
единицы. Единицы указывают, какие вершины
единичного квадрата принадлежат области
истинности соответствующей функции
.
Поскольку строка
содержит одни нули, то область истинности
данной функции (константы «ложь») –
пустое множество. В строке
только одна единица, соответствующая
вершине
 с номером 3 единичного квадрата
с номером 3 единичного квадрата
 ,
и, следовательно, областью истинности
для конъюнкции будет подмножество
,
и, следовательно, областью истинности
для конъюнкции будет подмножество
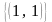 .
.
Таблица 5.1
|
0 |
1 |
2 |
3 |
Название функции |
Обозначение |
|
0 |
0 |
1 |
1 |
||
|
0 |
1 |
0 |
1 |
||
|
0 |
0 |
0 |
0 |
константа «ложь» |
0 |
|
0 |
0 |
0 |
1 |
конъюнкция (логическое умножение) |
|
|
0 |
0 |
1 |
0 |
запрет ( запрещает ) |
|
|
0 |
0 |
1 |
1 |
пустая операция над |
|
|
0 |
1 |
0 |
0 |
запрет ( запрещает ) |
|
|
0 |
1 |
0 |
1 |
пустая операция над |
|
|
0 |
1 |
1 |
0 |
сложение по модулю 2 |
|
|
0 |
1 |
1 |
1 |
дизъюнкция (логическое сложение) |
|
|
1 |
0 |
0 |
0 |
стрелка Пирса |
|
|
1 |
0 |
0 |
1 |
эквиваленция |
|
|
1 |
0 |
1 |
0 |
инверсия (отрицание ) |
|
|
1 |
0 |
1 |
1 |
импликация ( влечет ) |
|
|
1 |
1 |
0 |
0 |
инверсия (отрицание ) |
|
|
1 |
1 |
0 |
1 |
импликация ( влечет ) |
|
|
1 |
1 |
1 |
0 |
штрих Шеффера |
|
|
1 |
1 |
1 |
1 |
константа «истина» |
1 |














10
00
11
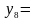
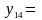
011
00
10
11
011

 1 3
1 3



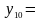




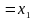
0 2 0 2

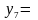


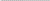
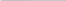

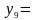
Рис. 5.7. Области истинности для Рис. 5.8. Области истинности
функций y2, y7, y8, y9 для функций y3, y10, y14
На
рис. 5.7 и 5.8 пунктирной линией показаны
границы областей истинности для
конъюнкции, сложения по модулю 2,
дизъюнкции, стрелки Пирса, импликации
,
эквиваленции и запрета
(сравните выделенные области с
соответствующими строками
,
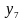 ,
,
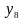 ,
,
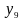 ,
,
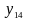 ,
,
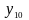 ,
,
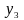 нашей таблицы).
нашей таблицы).
Собственно
бинарных функций в табл. 1 только десять,
т.к.
и
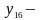 логические константы (0 и 1), а
логические константы (0 и 1), а
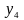 ,
,
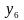 ,
,
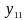 и
и
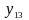 - унарные
функции,
т.е. функции одной переменной, из которых
практический интерес представляет лишь
одна унарная булева функция
- унарные
функции,
т.е. функции одной переменной, из которых
практический интерес представляет лишь
одна унарная булева функция
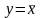 ,
называемая инверсией (отрицанием)
переменной.
,
называемая инверсией (отрицанием)
переменной.
Итак, в качестве простейших булевых функций мы получили две логические константы, одну унарную и десять бинарных функций. Ниже покажем, что изначальных булевых функций, из которых строятся все остальные, гораздо меньше.
Вопросы для самоконтроля
По табл. 5.1 определите области истинности для функций
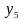 и
и
 .
.Область истинности какой функции равна объединению областей истинности конъюнкции и сложения по модулю два?
Область истинности какой функции равна пересечению областей истинности эквиваленции и дизъюнкции?
5.2.2. Булевы формулы
Полученные выше логические операции соединения можно выразить через три основные булевы функции: инверсию, конъюнкцию и дизъюнкцию, т.е. через те логические операции, которыми мы уже давно пользуемся при составлении сложных условий. Из табл. 5.1 следуют правила отрицания (инверсии), логического умножения (конъюнкции) и логического сложения (дизъюнкции), которые можно представить отдельной таблицей.
Таблица 5.2
-
1
1
0
0
1
1
1
0
0
1
0
1
0
1
1
0
0
1
0
0
1
1
0
0
Подставляя
в конъюнкции вместо переменной
ее инверсию (осуществляя композицию
конъюнкции и инверсии), получим новую
булеву функцию
.
Согласно табл. 5.2 областью истинности
данной функции будет множество
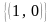 .
Только на вершине
.
Только на вершине
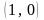 эта функция имеет значение единицы, а
на всех остальных вершинах единичного
квадрата она обращается в нуль. Но ту
же область истинности имеет и запрет
,
т.е. данные функции одно и то же. Поэтому
эта функция имеет значение единицы, а
на всех остальных вершинах единичного
квадрата она обращается в нуль. Но ту
же область истинности имеет и запрет
,
т.е. данные функции одно и то же. Поэтому
= = . (5.19)
Иначе говоря, мы выразили функцию через конъюнкцию и дизъюнкцию формулой (5.19). Аналогично можно выразить и другие булевы функции, область истинности которых содержит только одну вершину единичного квадрата. Получим
= = , (5.20)
= = . (5.21)
Замечание 1. Из полученных результатов следует очень простое правило получения формул, использующих операции инверсии и конъюнкции, для аналитического выражения булевых функций с областью истинности из одной вершины единичного квадрата. Формула эта строится по координатам той самой вершины:– единица заменяется соответствующей переменной, а нуль ее инверсией, и берется их конъюнкция.
5.2.3. Совершенные дизъюнктивные нормальные формы
Распространим
полученные результаты предыдущего
параграфа на
-арные
булевы функции. Функция
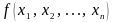 выделяет на гиперкубе
некоторое подмножество вершин – область
истинности этой функции.
выделяет на гиперкубе
некоторое подмножество вершин – область
истинности этой функции.
Если
эта область содержит только одну вершину
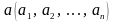 ,
то согласно установленному выше правилу
(замечание
1,
п. 5.2.2) формулу данной функции можно
построить по координатам данной вершины.
Такая формула будет представлять
конъюнкцию
булевых величин вида
,
то согласно установленному выше правилу
(замечание
1,
п. 5.2.2) формулу данной функции можно
построить по координатам данной вершины.
Такая формула будет представлять
конъюнкцию
булевых величин вида
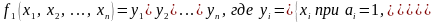 (5.22)
(5.22)
Такие формулы называются элементарными конъюнкциями длины .
Определение 21. Элементарная конъюнкция называется полной, если она является формулой для булевой функции (имеющей область истинности из одной только вершины гиперкуба). Длина полной элементарной конъюнкции всегда равна размерности гиперкуба. Если длина элементарной конъюнкции меньше , то она называется неполной.
Пусть
теперь некоторая функция
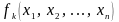 имеет область истинности, которая
состоит из
вершин гиперкуба
.
Координаты этих вершин можно записать
в матрице с числом строк
и числом столбцов
имеет область истинности, которая
состоит из
вершин гиперкуба
.
Координаты этих вершин можно записать
в матрице с числом строк
и числом столбцов
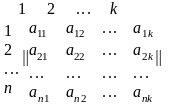
Такую матрицу называют булевой. Каждый из ее столбцов определяет координаты одной из вершин области истинности булевой функции . Тогда для данной функции можно построить следующую формулу:
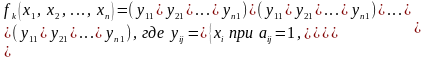 (5.23)
(5.23)
Определение 22. Формула (5.23) называется совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции . Она представляет собой дизъюнкцию всех полных конъюнкций для всех вершин области истинности этой функции.
Очевидно,
полная конъюнкция является частным
случаем совершенной ДНФ
(подобно тому, как столбец является
частным случаем матрицы). Поэтому можно
утверждать, что формулу (5.23) можно
построить для любой булевой функции,
имеющей непустую область истинности.
Иначе говоря, совершенная ДНФ существует
для любой булевой функции, кроме константы
«ложь». Однако эту константу можно
определить более простой формулой
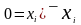 ,
использующей только две из трех основных
(теперь их так уже можно называть с
полным правом!) логических операций.
,
использующей только две из трех основных
(теперь их так уже можно называть с
полным правом!) логических операций.
Итак, основу мироздания булевых функций могут составлять всего лишь три простейшие логические операции – инверсия, конъюнкция и дизъюнкция. С помощью их различных композиций получаются любые другие булевы функции. Это означает, что система из данных трех логических операций является функционально полной системой булевых функций (см. далее).

111
011



Пример 5.9. Построить совершенную
ДНФ
для булевой функции
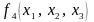 ,
001 101
,
001 101
область истинности которой есть передняя
 грань
куба
грань
куба
 (рис. 5.9). 010 110
(рис. 5.9). 010 110
Решение. Передняя грань содержит 4
вершины, координаты которых запишем в 000 100
булевой матрице
Рис.
5.9. Графическая интерпретация СДНФ

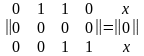 ,
,
которая, как показано выше, равна троичному вектору x0x, записанному здесь в виде вектор-столбца. Согласно (5.23) получим формулу
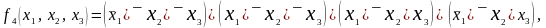
которая и будет ответом на поставленный вопрос.
Замечание 1. Для сокращения записи булевых формул допускается опускать символ дизъюнкции (подобно тому, как в элементарной алгебре опускается символ операции умножения).
Замечание 2. С помощью круглых скобок в алгебраических формулах задается порядок выполнения арифметических действий, а при отсутствии скобок порядок действий определяется согласно их приоритетам. Например, операция умножения имеет больший приоритет и выполняется раньше сложения. Так и конъюнкция (логическое умножение) имеет больший приоритет по отношению к дизъюнкции (логическому сложению). Потому в правой части равенства (5.23) круглые скобки можно опустить.
С учетом сделанных замечаний результат решения последнего примера может быть записан более компактно, а именно:
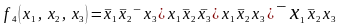 .
.
Будем придерживаться такой, более простой, формы записи булевых формул и дальше.
Пример 5.10. Найти совершенную ДНФ для булевой функции, областью истинности которой является первый слой куба (рис. 5.9).
Решение. Веса, равные единице, имеют следующие вершины данного куба: 001, 010, 100. Тогда по определению первым его слоем будет множество {001, 010, 100}. Составим для данной области булеву матрицу:
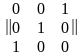 .
.
Первый
столбец данной матрицы задает полную
элементарную конъюнкцию –
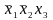 ,
второй –
,
второй –
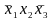 и третий –
и третий –
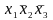 .
Тогда искомая ДНФ будет
.
Тогда искомая ДНФ будет
 .
.
Вопросы для самоконтроля
Определите совершенные ДНФ для двух функций, области истинности которых верхнее переднее и правое переднее ребра куба (рис. 5.8) соответственно. Затем получите ДНФ для функции с областью истинности, равной пересечению указанных выше ребер. Сравните полученные ДНФ.
Чему равна область истинности конъюнкции двух функций – объединению или пересечению их областей истинности?
Чему равна область истинности дизъюнкции двух функций – объединению или пересечению их областей истинности?
Что такое функционально полная система булевых функций?
Существуют ли такие булевы функции, которые нельзя выразить через дизъюнкцию, конъюнкцию и инверсию?
5.2.4. Булева алгебра
Данная
алгебра, носителем которой является
все множество булевых функций, а
сигнатурой
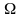 )
- три логические операции – инверсия,
конъюнкция и дизъюнкция, восходит к
трудам О. Де Моргана и Дж. Буля. Основные
же тождества этой алгебры непосредственно
следуют из табл. 5.1. Их можно использовать
при алгебраических преобразованиях
сложных булевых формул.
)
- три логические операции – инверсия,
конъюнкция и дизъюнкция, восходит к
трудам О. Де Моргана и Дж. Буля. Основные
же тождества этой алгебры непосредственно
следуют из табл. 5.1. Их можно использовать
при алгебраических преобразованиях
сложных булевых формул.
Пусть
,
и
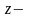 произвольные булевы функции. Тогда
тождества булевой алгебры будут иметь
следующий вид.
произвольные булевы функции. Тогда
тождества булевой алгебры будут иметь
следующий вид.
Свойства
коммутативности операций
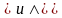 :
:
1а.
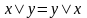 ,
1б.
,
1б.
 .
.
Свойства ассоциативности операций :
2а.
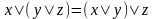 ,
2б.
,
2б.
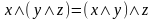 .
.
Свойства
дистрибутивности операций
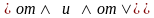 :
:
3а.
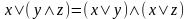 ,
,
3б.
 .
.
Свойства нуля и единицы:
4а.
 - определение
единицы,
- определение
единицы,
4б.
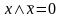 - определение
нуля,
- определение
нуля,
5а.
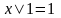 ,
5б.
,
5б.
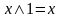 ,
,
6а.
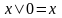 ,
6б.
,
6б.
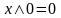 ,
,
7а.
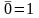 ,
7б.
,
7б.
 .
.
Свойства идемпотентности операций :
8а.
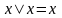 ,
8б.
,
8б.
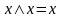 .
.
Законы поглощения:
9а.
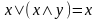 ,
9б.
,
9б.
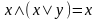 .
.
Законы Де Моргана:
10а.
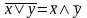 ,
10б.
,
10б.
 .
.
Сравнивая
эти тождества с тождествами алгебры
множеств, получаем полное их совпадение
(с точностью до обозначения операций).
Это совпадение объясняется тем, что
любая булева функция по существу есть
символ некоторого подмножества гиперкуба
,
которое является ее областью истинности.
При этом дизъюнкция двух булевых функций
будет означать операцию объединения
их областей истинности, а конъюнкция –
операцию пересечения этих областей.
Универсумом в данном случае является
гиперкуб
.
Булева функция, областью истинности
которой является весь гиперкуб, - это
константа «истина», т.е. 1. А булева
функция, область истинности которой
пустое множество, - это константа «ложь»,
т.е. 0. Дополнение области истинности
функции
на гиперкубе
является областью ложности этой функции,
т.е. областью истинности противоположной
булевой функции
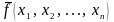 .
Поэтому операция инверсии равносильна
операции дополнения над ее областью
истинности.
.
Поэтому операция инверсии равносильна
операции дополнения над ее областью
истинности.
Из данного сравнения следует, что булева алгебра и алгебра множеств суть одна и та же алгебра. В самом широком смысле алгебра называется булевой, если для нее выполняются тождества 1а – 10б независимо от природы элементов носителя и обозначения трех ее основных операций.
Рассмотрим несколько примеров на алгебраические преобразования булевых формул.
Пример 5.11. Упростить выражение ( ) ( ) ( ).
Решение. Используя тождества 1б, 2а и 3б, получим
((
)
(
))
(
)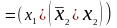 (
).
(
).
Откуда на основании 1а, 4а, 5б, 3а, 4а, 1б и 5б имеем
(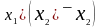 )
(
)
(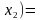 (
(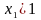 )
(
(
)
(
(
 (
(
![]()
![]() (
(
(
(
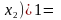 .
.
Таким
образом, (
![]() )
(
)
(
)
)
(
)
(
)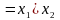 .
Теперь сравним полученный результат с
табл. 5.1.
.
Теперь сравним полученный результат с
табл. 5.1.
Пример 5.12. Упростить совершенную ДНФ для импликации.
Решение.
Согласно табл. 5.1 импликация может быть
определена по формуле
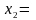 (
)
(
)
(
).
(
)
(
)
(
).
Упростим правую часть равенства. Применяя тождества 3б, 1а, 4а, 1б, 5б, 3а, 1а, 4а, 1б и 5б, получим
(
)
(
)
(
(
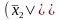 ))
(
))
(
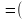
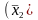
 ))
(
(
))
(
(
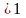 )
(
)
(
 (
(
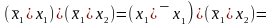
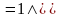
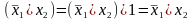 .
.
Таким образом, искомая формула будет
 .
(5.24)
.
(5.24)
Правая часть равенства (5.24) представляет конъюнкцию неполных дизъюнкций. Такие формулы называются сокращенными ДНФ. В примерах 5.11 и 5.12 был осуществлен переход от совершенных ДНФ к сокращенным. Сокращенные ДНФ можно задавать также матрицами, только матрицы эти будут уже не булевыми (как в случае ДНФ), а троичными. Ее столбцы - это троичные векторы, каждый из которых в общем случае может определять грань гиперкуба. Например, троичные матрицы для сокращенных ДНФ, полученных в примерах 3 и 4, будут такими:
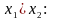
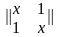 ,
,
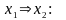
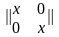 .
.
Здесь первый столбец первой матрицы определяет грань 1x размерности 1, т.е. ребро с вершинами 10 и 11. Аналогично второй столбец x1={01, 11} и столбцы второй матрицы 0x={00, 01}, x1={01, 11}.
Напомним, что число символов «x» в троичном векторе определяет размерность грани. Например, грань 1xx куба имеет размерность 2 и представляет собой множество {100, 101, 110, 111}, что соответствует четырем столбцам булевой матрицы. Поэтому троичные матрицы по сравнению с булевыми более компактно описывают одну и ту же булеву функцию.
Вопросы для самоконтроля
Постройте булеву матрицу для совершенной ДНФ ( ) ( ) ( ) (
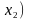 .
Затем с помощью алгебраических
преобразований определите сокращенную
ДНФ и постройте для нее троичную матрицу.
Сравните результаты.
.
Затем с помощью алгебраических
преобразований определите сокращенную
ДНФ и постройте для нее троичную матрицу.
Сравните результаты.Для функции
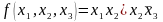 найдите совершенную ДНФ.
найдите совершенную ДНФ.Дайте объяснение тому, что двойная инверсия - пустая операция.
5.2.5. Конъюнктивные нормальные формы
Наряду с совершенными и сокращенными ДНФ в булевой алгебре используются также совершенные и сокращенные конъюнктивные нормальные формы (КНФ), которые также могут задаваться в виде матриц.
Пример. 5.13. Дана функция
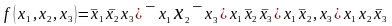 .
(5.25)
.
(5.25)
Найти совершенную ДНФ для инверсии данной функции.
Решение.
Функция
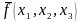 имеет область истинности, равную области
ложности заданной функции
имеет область истинности, равную области
ложности заданной функции
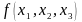 .
Область истинности этой функции согласно
(5.25) представлена следующими пятью
вершинами {001,
010, 100, 101,
110}.
Тогда ее область ложности будет содержать
все остальные вершины куба
(рис. 5.9), т.е. множество {000,
011, 111}
– ее область ложности и область истинности
функции
.
Значит булева матрица функции
имеет вид
.
Область истинности этой функции согласно
(5.25) представлена следующими пятью
вершинами {001,
010, 100, 101,
110}.
Тогда ее область ложности будет содержать
все остальные вершины куба
(рис. 5.9), т.е. множество {000,
011, 111}
– ее область ложности и область истинности
функции
.
Значит булева матрица функции
имеет вид
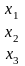
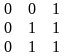 ,
откуда
,
откуда
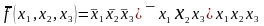 .
.
Пример 5.14. Используя законы Де Моргана (10а, 10б), выразить функцию из предыдущего примера в виде конъюнкции дизъюнкций.
Решение. Поскольку двойная инверсия - пустое преобразование, то

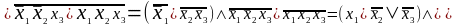
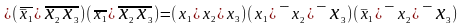 .
.
Полученная формула для функции (5.25) называется совершенной КНФ. Ее можно строить по области ложности функции по следующему правилу.
Если область ложности состоит из вершин, то записывается конъюнкция одинаковых дизъюнкций из всех переменных (полных элементарных дизъюнкций), от которых зависит функция. Затем ставится знак инверсии над теми переменными, которые соответствуют координатам вершин, равным единице.
Для нашего примера областью ложности было множество {000, 011, 111}. Поэтому
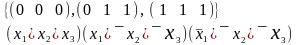
Совершенную КНФ не имеет только одна булева функция – константа «истина», т.к. ее область ложности - пустое множество.
Конъюнкции из неполных дизъюнкций образуют сокращенную ДНФ.
Например,
формула
 будет уже сокращенной ДНФ, т.к. одна из
ее дизъюнкций неполная (во второй
дизъюнкции отсутствует переменная
).
будет уже сокращенной ДНФ, т.к. одна из
ее дизъюнкций неполная (во второй
дизъюнкции отсутствует переменная
).
Сокращенные КНФ нашли применение в алгоритмах исчисления предикатов методом резолюций. На основе данного метода разработан транслятор языка программирования ПРОЛОГ. Этот язык программирования [1] имеет большое сходство с языком логики предикатов, основные языковые формы которого будут рассматриваться в следующей главе.
На
множестве функций сравнения можно
построить и другие алгебры, например,
существует так называемая алгебра
Жегалкина с сигнатурой
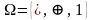 ,
позволяющая выразить любую двухзначную
логическую функцию и выполнять
преобразования. Здесь мы вплотную
подходим к понятию базиса логических
функций.
,
позволяющая выразить любую двухзначную
логическую функцию и выполнять
преобразования. Здесь мы вплотную
подходим к понятию базиса логических
функций.
Вопросы для самоконтроля
Определите совершенные ДНФ и КНФ функции, область истинности которой пересечение двух граней 1xx0 и x1x0.
Какая функция имеет следующую совершенную КНФ
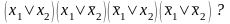
Определите совершенные КНФ для эквивалентности и сложения по модулю 2.
5.2.6. Классы булевых функций. Понятие базиса
Существует строгое формальное доказательство того, что любую булеву функцию можно выразить через определенный набор других функций, т.е. представить в некотором базисе.
Определение 23. Система переключательных функций {f1, f2, ..,fk} является полной в классе B и называется базисом в том случае, если любая переключательная функция fB может быть представлена посредством функций f1, f2, ..,fk с использованием перенумерации аргументов или подстановки.
Для доказательства этого факта рассмотрим некоторые классы булевых функций, обладающие определенными свойствами.