

1. Вещественные числа. Грани числового множества. Теорема о существовании точной верхней и
нижней граней. Операции над вещественными числами. Свойства операций.
Вещественные числа
Вещественные числа – множество всевозможных десятичных дробей.
Вещественные числа, не являющиеся рациональными, принято называть иррациональными.
Операции над вещественными числами
Сложение, вычитание, деление, умножение и возведение в степень.
Свойства операций
Для вещественных чисел справедливы все основные свойства рациональных чисел.
Правило сравнения:
1°. если > и > , то > если = и = , то =
Правила сложения:
2°. + = + (переместительное свойство)
3°. ( + ) + = + ( + ) 4°. + 0 =
5°. + ′ = 0 (′ – противоположное число)
Правила умножения:
6°. = (переместительное свойство)
7°. ( ) = ( ) (сочетательное свойство)
8°. 1 =
9°. ′ = 1 (′ – обратное число)
10°. ( + ) = + (распределительное свойство)
11°. Если > , то + > + 12°. Если > и > 0, то > 13°. Аксиома Архимеда:
Каково бы не было рациональное число , можно число 1 повторить слагаемым столько раз, что полученная сумма превзойдёт .
Грани числового множества
1)Множество вещественных чисел называется ограниченным сверху, если существует такое вещественное число, что каждый элемент удовлетворяет неравенству ≤ (число – верхняя грань множества).
2)Множество вещественных чисел называется ограниченным снизу, если существует такое вещественное число, что каждый элемент удовлетворяет неравенству ≥ (число – верхняя грань множества).
Теорема о существовании точной верхней и нижней грани
1)Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху, то существует вещественное число , которое является точной верхней гранью этого множества.
Наименьшая верхняя грань: = sup{ }. (от сл. “супремум”)
2)Если множество вещественных чисел содержит хотя бы один элемент и ограничено снизу, то существует вещественное число число , которое является точной нижней гранью этого множества.
Наибольшая нижняя грань: = inf{ }. (от сл. “инфинум”)
2. Понятие комплексного числа. Различные формы записи. Арифметические операции над
комплексными числами, возведение в степень и извлечение корня.
Понятие комплексного числа
Комплексное число – упорядоченная пара ( , ) вещественных чисел, первое из которых называется действительной частью, а второе – мнимой частью. 2 = −1, | | = √ 2 + 2
Формы записи
1)Алгебраическая: = +
2)Тригонометрическая: = | | (cos + sin )
3)Показательная: = | |

Арифметические операции
1) Сумма
= (1 + 2, 1 + 2)
2) Разность
= (1 − 2, 1 − 2)
3) Произведение
= (1 2 − 1 2, 1 2 + 2 1)
4) Частное
= ( |
1 2 + 1 2 |
|
, |
2 1 − 1 2 |
) |
|
|
||||||||
2 |
+ 2 |
|
|
2 |
+ 2 |
|
|
||||||||
|
|
|
2 |
2 |
|
|
|
2 |
2 |
|
|
|
|||
Возведение в степень |
|
|
|
|
|
||||||||||
По формуле Муавра: |
|
|
|
|
|
||||||||||
= | | (cos + sin ) |
|
|
|||||||||||||
Извлечение корня |
|
|
|
|
|
|
|||||||||
По формуле Муавра: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
+ 2 |
|
+ 2 |
|
|||||
√ = |
√| | (cos |
|
|
|
|
|
+ sin |
|
) |
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Грани числового множества. Теорема о существовании точной верхней и нижней граней. Принцип
вложенных отрезков.
Грани числового множества
1)Множество вещественных чисел называется ограниченным сверху, если существует такое вещественное число, что каждый элемент удовлетворяет неравенству ≤ (число – верхняя грань множества).
2)Множество вещественных чисел называется ограниченным снизу, если существует такое вещественное число, что каждый элемент удовлетворяет неравенству ≥ (число – нижняя грань множества).
Теорема о существовании точной верхней и нижней грани
1)Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху, то существует вещественное число , которое является точной верхней гранью этого множества.
Наименьшая верхняя грань: = sup{ }. (от сл. “супремум”)
2)Если множество вещественных чисел содержит хотя бы один элемент и ограничено снизу, то существует вещественное число число , которое является точной нижней гранью этого множества.
Наибольшая нижняя грань: = inf{ }. (от сл. “инфинум”)
Принцип вложенных отрезков.
Лемма о вложенных отрезках (принцип Коши – Кантора):
Для любой последовательности вложенных отрезков существует точка, принадлежащая всем этим отрезкам. Если длины отрезков стремятся к нулю, то такая точка единственная.
4. Понятие числовой последовательности. Монотонные и ограниченные последовательности. Бесконечно малые и бесконечно большие числовые последовательности, их свойства. Сходящиеся последовательности. Ограниченность, единственность предела. Арифметические действия с пределами.
Понятие числовой последовательности
Числовая последовательность – упорядоченное множество чисел.
Монотонные последовательности
Последовательность называется возрастающей, если каждый её элемент больше предыдущего. Последовательность называется убывающей, если каждый её элемент меньше предыдущего.
Ограниченные последовательности
Последовательность называется ограниченной, если она ограничена сверху и снизу.

Бесконечно малые и бесконечно большие последовательности
Бесконечно малая последовательность – последовательность, стремящаяся к нулю. Бесконечно большая последовательность – последовательность, стремящаяся к бесконечности.
Свойства бесконечно малых и бесконечно больших последовательностей:
1°. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. 2°. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность. 3°. Бесконечно малая последовательность ограничена.
4°. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Сходящаяся последовательность
Сходящаяся последовательность – последовательность элементов некоторого множества, которая имеет конечный предел.
Ограниченность предела
Сходящаяся последовательность имеет только один предел.
Единственность предела
Сходящаяся последовательность ограничена.
Арифметические действия с пределами:
1) Сумма и разность:
lim ( ± ) = lim ± lim
→∞ |
→∞ |
→∞ |
2) Вынесение числа за предел:
lim ( ) = lim
→∞ →∞
3) Произведение:
lim ( ) = lim lim
→∞ →∞ →∞
4) Частное:
|
|
|
lim |
lim |
= |
→∞ |
|
|
lim |
||
→∞ |
|
||
|
|
→∞ |
|
5. Предельный переход в неравенствах. Теорема о пределе двух последовательностей. Теорема “о двух
милиционерах”.
Предельный переход:
Если элементы сходящейся последовательности { } удовлетворяют неравенству ≥ ( ≤ ), то пределэтой последовательности удовлетворяет неравенству ≥ ( ≤ ).
Теорема о пределе двух последовательностей
{ }, { } – сходящиеся последовательности. Пусть lim = и lim = . Пусть, начиная с некоторого
→∞ →∞
номера, элементы последовательности { } удовлетворяют неравенствам ≤ ≤ . Тогда lim = .
→∞
Теорема о двух милиционерах
Если одна последовательность заключена между двумя другими, имеющими одинаковый предел, то она имеет
тот же предел. |
|
|
|
|||||
|
|
|
≤ |
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
lim |
= → |
lim |
= |
||||
|
→∞ |
|
|
→∞ |
|
|
||
|
|
lim |
= |
|
|
|||
|
|
|
|
|
||||
|
→∞ |
|
|
|
|
|
||
|
|
|
|
|
|
|||

6. Теорема о монотонной и ограниченной последовательности. Число “e”.
Теорема о монотонной и ограниченной последовательности
Если монотонная последовательность { } ограничена с обеих сторон, то она сходится.
Число “e”
Число “e” (число Эйлера) – иррациональное число или математическая константа, являющееся основанием степени показательной функции, а также основанием натурального логарифма. Число является примером сходящейся монотонной последовательности.
|
1 |
|
|
= lim (1 + |
|
) |
|
|
|||
→∞ |
|
||
≈ 2,7182 |
|
|
7. Подпоследовательности. Свойства. Верхний и нижний предел. Примеры.
Подпоследовательность
Подпоследовательность – построенная по такому же правилу последовательность, взятая из начальной общей последовательности.
Свойства
1°. Если подпоследовательность сходится к числу , то и любая другая подпоследовательность сходится к этому числу.
2°. Каждая последовательность бесконечно большой подпоследовательности также будет бесконечно большой. 3°. Из каждой бесконечно большой последовательности можно выделить монотонную бесконечно большую последовательностью
Верхний и нижний предел
1) Наибольшая предельная точка последовательности называется верхним пределом этой последовательности и
обозначается как = lim .
→∞
2) Наименьшая предельная точка последовательности называется нижним пределом этой последовательности и
обозначается как = lim .
→∞
Примеры
1)последовательность простых чисел является подпоследовательностью последовательности натуральных чисел
2)последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел
8. Теорема Больцано-Вейерштрасса. Следствия.
Теорема
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Следствия
1)Из любой ограниченной последовательности можно выделить монотонную последовательность.
2)Пусть { } – ограниченная последовательность, элементы которой находятся на сегменте [ , ]. Тогда предел с любой сходящейся последовательность { } также находится на сегменте [ , ].
9. Критерий Коши сходимости последовательности.
Критерий Коши
Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
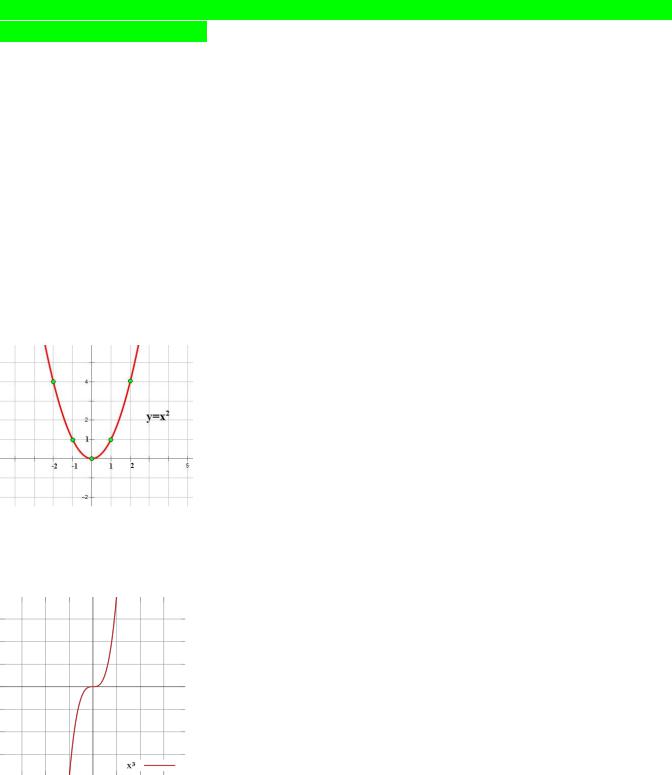
10. Понятие функции. Монотонные, четные, нечетные, ограниченные, неограниченные, сложные,
обратные функции. Примеры.
Функция
Переменная является функцией переменной , если каждому значению переменной ставится в соответствие определенное значение переменной (где – аргумент, – частное значение).
Монотонные функции
1) Возрастающая функция – функция, у которой большему значению аргумента соответствует большее значение функции: ( 2) > ( 1)
Пример: = 9 − 4
2) Убывающая функция – функция, у которой большему значению аргумента соответствует меньшее значение
функции: ( 2) < ( 1)
Пример: = 1 − 3
Четная функция
Четная функция – функция называется четной, если для любого из области определения выполняется равенство (− ) = ( ). График симметричен относительно оси ординат.
Пример: = 2
Нечетная функция
Нечетная функция – функция называется нечетной, если для любого из области определения выполняется равенство (− ) = − ( ). График симметричен относительно начала координат.
Пример: ( ) = 3
Ограниченная и неограниченная функция
Функция называется ограниченной, если существует такое положительное число , что | ( )| ≤ для всех .
Пример: ( ) = sin
Если такого числа не существует, то функция неограниченная.
Пример: ( ) = 2 + 1
Сложная функция
Функция = ( ( )) называется сложной, если она составлена из 2-х или более простых функций.
Пример: ( ) = cos 5
Обратная функция
Функция = −1( ) называется обратной для функции = ( ).
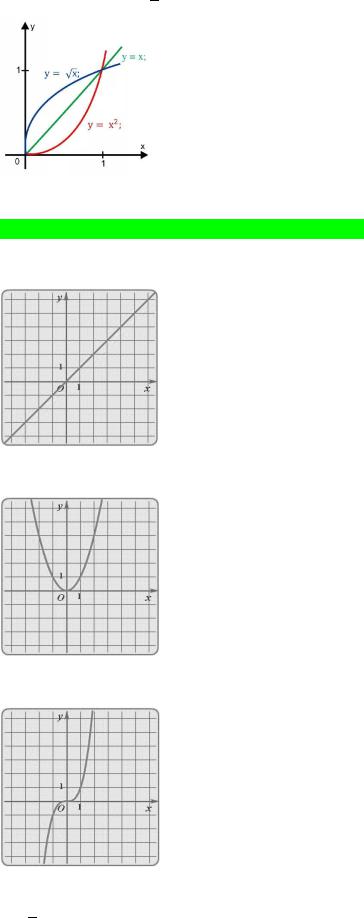
Пример: функция = √ является обратной для функции = 2
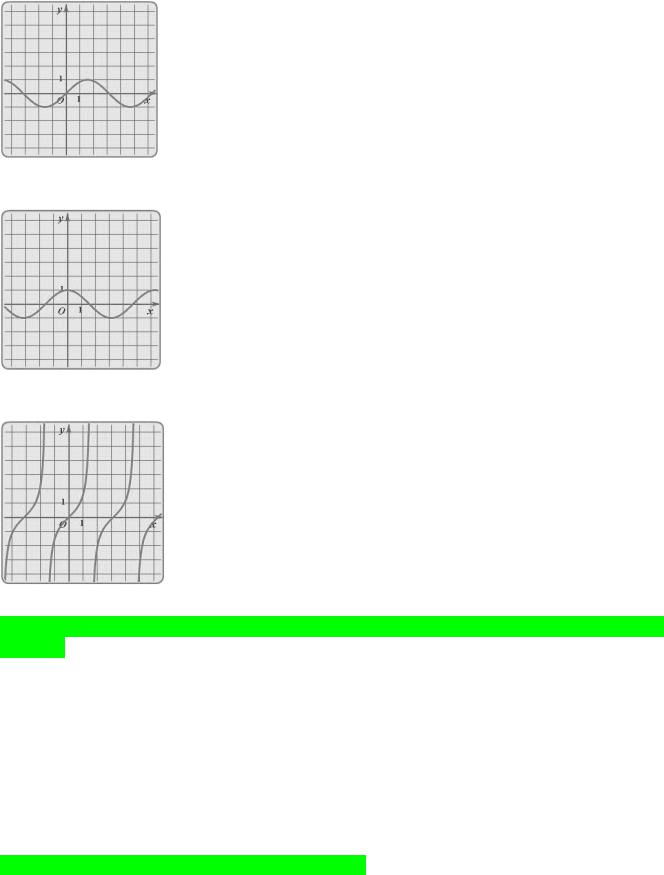
11. Простейшие элементарные функции. Их графики.
1) Прямая
= +
2) Парабола
= 2
3) Кубическая парабола
= 3
4) Гипербола
=

5) Степенная
= √
6) Показательная
=
7) Логарифмическая
= log
8) Синусоида
= sin
9) Косинусоида
= cos
10) Тангенсоида
= tg
12. Предел функции в точке. Эквивалентность определений по Коши и по Гейне. Односторонние
пределы.
Предел функции
Предел функции – величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
Односторонний предел
Односторонник предел – предел числовой функции, подразумевающий приближение к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределом.
Эквивалентность определений
Определения предела функции по Коши и по Гейне эквивалентны.
13. Критерий Коши существования предела функции.
Пусть – числовая последовательность, тогда она имеет предел тогда и только тогда, когда удовлетворяет условию Коши: > 0 , > : | − | <

14. Свойства пределов функции в точке.
1)Если функция имеет предел, то только один.
2)Вынос константы:
lim =
→
3) Предел суммы и разности:
lim( ± ) = lim ± lim
→ → →
4) Предел произведения: lim( ) = lim lim
→ |
|
|
→ |
→ |
|
5) Предел частного: |
|
||||
|
|
|
lim |
|
|
lim |
= |
→ |
|
|
|
|
lim |
|
|||
→ |
|
|
|||
→
15. Первый замечательный предел.
lim sin = 1
→0
16. Второй замечательный предел.
|
1 |
|
|
||
lim (1 + |
|
|
) |
= |
|
|
|||||
→∞ |
|
|
|||
|
|||||
17. Бесконечно малые и бесконечно большие функции. |
|||||
Бесконечнно малая функция
Функция называется бесконечно малой, если функция имеет предел и он равен нулю: lim ( ) = 0
→0
Бесконечно большая функция
Функция называется бесконечно большой, если она имеет предел и он равен бесконечности: lim ( ) = ∞
→0
18. Применение эквивалентных бесконечно малых к вычислению пределов.
Для раскрытия неопределённостей часто применяют принцип замены бесконечно малых эквивалентными при стремлении аргумента к нулю. Например, sin ~ при → 0; tg ~ при → 0. Обычно данные берут из таблицы эквивалентных бесконечно малых.
19. Теорема о пределе монотонных функций.
Если функция ( ) монотонна и ограничена при < 0 |
или при > 0, то существует соответственно её левый |
предел lim ( ) = ( 0 − 0) или её правый предел |
lim ( ) = ( 0 + 0). |
→0−0 |
→0+0 |
20. Непрерывность функции в точке. Определения по Коши и Гейне, непрерывность слева и справа.
Свойства непрерывных функций.
Непрерывность функции в точке
Функция = ( ) называется непрерывной в точке 0, если существует предел функции в этой точке и он равен
значению функции в этой точке: lim ( ) = ( 0).
→0
Определение по Коши
Функция называется непрерывной в точке 0, если > 0, > 0, , | − 0| < : | ( ) − ( 0)| <
Определение по Гейне |
|
|
|
|
|
|
|||
Функция называется непрерывной в точке , если для любой последовательности { |
}∞ |
, |
|
, такого, что |
|||||
|
|
|
|
0 |
|
=1 |
|
|
|
lim |
= : |
lim ( ) = ( ) |
|
|
|
|
|
||
→∞ |
0 |
→∞ |
|
0 |
|
|
|
|
|
Непрерывность справа |
|
|
|
|
|
|
|||
Если односторонний предел |
lim ( ) = ( 0), то функция называется непрерывной справа. |
|
|
||||||
|
|
|
|
→ +0 |
|
|
|
|
|
Непрерывность слева |
|
|
( |
) |
= (0), то функция называется непрерывной слева. |
Если односторонний предел lim |
|
|
→ −0 |
|
|
Свойства непрерывных функций
1) Если даны две непрерывные функции в точке 0, то их сумма, разность и произведение являются непрерывной функцией.
2) Основные элементарные функции непрерывны в своей области определения.
3) Функция является непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
4) Если функции ( ) и ( ) непрерывны на и ( ) ≠ 0, , то частное ( ) – непрерывное на множестве
( )
функции.
21. Разрывные функции. Классификация точек разрыва. Примеры.
Разрывные функции
Разрывные функции – функции, имеющие разрыв в некоторых точках. Если функция монотонна, то она имеет разрыв только 1-ого рода.
Точка разрыва
Точка называется точкой разрыва функции ( ), если ( ) не определена в точке или определена, но не является в ней непрерывной.
Классификация точек разрыва:
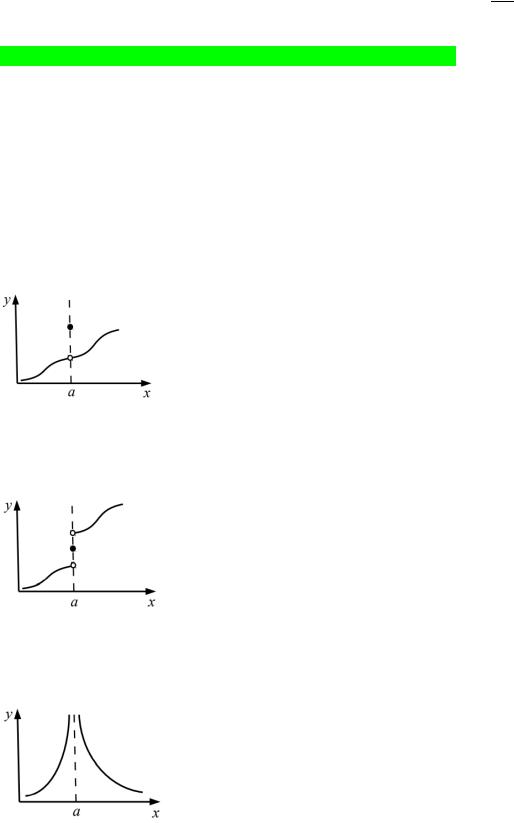
1) Устранимый разрыв Если точка – точка разрыва первого рода и ( − 0) = ( + 0), то точка – точка устранимого разрыва.
Пример:
2) Разрыв 1-ого рода Если функция имеет правые и левые конечные пределы и они не равны друг другу, то точка – точка разрыва первого рода.
Пример:
3) Разрыв 2-ого рода Если хотя бы одно предельное значение слева или справа бесконечно или не существует, то точка – точка разрыва второго рода.
Пример:
