Параметрические уравнения прямой в пространстве:

Если известна точка , принадлежащая прямой, и направляющий вектор  данной прямой, то параметрические уравнения этой прямой задаются системой:

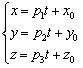
Прямая, заданная пересечением двух плоскостей

Если плоскости   пересекаются, то система линейных уравнений  задаёт прямую в пространстве.

То есть прямая задана уравнениями двух плоскостей.

Пример задачи

Переписать уравнения прямой в каноническом виде:

Решение: Чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор.

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. В системе уравнений нужно обнулить какую-нибудь координату. Пусть , тогда получаем систему двух линейных уравнений с двумя неизвестными: .

Почленно складываем уравнения и находим решение системы:

Таким образом, точка  принадлежит данной прямой.

Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут быть пересекающимися, параллельными и скрещивающимися.

Пересекающиеся прямые Две различные прямые называются пересекающимися, если они имеют общую точку. Точка пересечения единственна: если две прямые имеют две общие точки, то они совпадают. Существует единственная плоскость, проходящая через две пересекающиеся прямые.

Параллельные прямые

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые Если две прямые пересекаются или параллельны, то, как мы видели, через них можно провести плоскость (и притом единственную). Возможна также ситуация, когда через две прямые плоскость провести нельзя. Две прямые называются скрещивающимися, если они не параллельны и не пересекаются. Равносильное определение: две прямые называются скрещивающимися, если они не лежат в одной плоскости.

15.Расстояние от точки до плоскости. Расстояние от точки до прямой и расстояние между скрещивающимися прямыми.

Расстояние от точки до прямой/плоскости — равно длине перпендикуляра, опущенного из точки на прямую/плоскость.

Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(M_x, M_y, M_z) до плоскости можно найти, используя следующую формулу:

d =	|A·Mx + B·My + C·Mz + D|
	√A2 + B2 + C2

Расстояния от точки до прямой на плоскости:

Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(M_x, M_y) до прямой можно найти, используя следующую формулу

d =	|A·Mx + B·My + C|
	√A2 + B2

Расстояние от точки до прямой в пространстве:

Если задано уравнение прямой L, то s = {m; n; p} - направляющий вектор прямой и M₁(x₁, y₁, z₁) - координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

S = |M₀M₁×s|.

Площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

S = |s|d.

Высота равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s.

Если s = {m; n; p} - направляющий вектор прямой l, M₁(x₁, y₁, z₁) - точка лежащей на прямой, тогда расстояние от точки M₀(x₀, y₀, z₀) до прямой l можно найти, используя формулу

M₀M₁ = {x₁-x₀; y₁-y₀;z₁-z₀}; M₀M₁×s – векторное произведение;

d =	|M0M1×s|
	|s|

16.Нормальное уравнение плоскости. Отклонение точки от плоскости. Теорема о свойствах отклонения точки от плоскости.

Нормальное уравнение плоскости.

cos α·x+cos β·y+cos γ·z-p=0 называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде.

(вектор нормали)n=(cos α, cos β, cos γ) .

Отклонение точки от плоскости.

Отклонение точки от плоскости с уравнением находится по формуле:

Отклонением данной точки от данной плоскости называется число d, равное длине перпендикуляра, опущенного из этой точки на плоскость, взятой со знаком плюс, если точка и начало координат лежат по разные стороны от данной плоскости, и со знаком минус, если они лежат по одну сторону от плоскости. Очевидно, что расстояние от точки до плоскости равно абсолютной величине отклонения.

Теорема о свойствах отклонения точки от плоскости.

Теорема 2

Отклонение точки от плоскости с уравнением (43) находится по формуле: (44).

Доказательство:

Докажем: .

, т.к. .

1. , когда направлен в то полупространство, где нет точки O.

2.

Теорема доказана