Сводимости, возникающие при доказательстве методом локальной замены, достаточно нетривиальны, чтобы их всегда можно было с гарантией представить в стандартном виде, однако они остаются относительно несложными.

Метод построения компонент (Component design method) — один из трех общих методов доказательства, которые часто встречаются и могут подсказать путь к доказательству NP полноты новой задачи. Другие два — это метод локальной замены и метод сужения задачи. Является наиболее сложным из упомянутых выше методов доказательства NP полноты.

19. Проблема Кука.

В теории алгоритмов вопрос о равенстве классов сложности P и NP является одной из центральных открытых проблем уже более трех десятилетий. Если на него будет дан утвердительный ответ, это будет означать, что теоретически возможно решать многие сложные задачи существенно быстрее, чем сейчас.

Проблема равенства классов P и NP является одной из семи задач тысячелетия, за решение которой Математический институт Клэя назначил премию в миллион долларов США.

Нестрого говоря, проблема равенства P = NP состоит в следующем: если положительный ответ на какой­то вопрос можно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно быстро найти (за

полиномиальное время и используя полиномиальную память)? Другими словами, действительно ли решение задачи проверить не легче, чем его отыскать? Например, верно ли, что среди чисел {−2, −3, 15, 14, 7, −10, …} есть такие, что их сумма равна 0 (задача о суммах подмножеств)? Ответ да, потому что −2 −3 + 15 −10 = 0 легко проверяется несколькими сложениями (информация, необходимая для проверки положительного ответа, называется сертификатом). Следует ли отсюда, что так же легко подобрать эти числа? Проверить сертификат так же легко, как найти его? Кажется, что подобрать числа сложнее, но это не доказано.

20. Булевы функции.

Булева функция от n аргументов — отображение Bn → B, где B = {0,1} —булево множество.

Функции

1.отрицание,

2.конъюнкция

3.дизъюнкция

4.импликация

5.эквивалентность

6.стрелка Пирса

7.штрих Шеффера

Простой конъюнкцией или конъюнктом называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза.

Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Элементарная конъюнкция. (Аналогично КНФ)

.

21. Схемы из функциональных элементов.

Схема из ФЭ — математическая модель вычислителя булевой функции, представленной некоторой формулой, собранного из структурных элементов, каждый из которых вычисляет одну из "базисных" булевых функций.

3 типа ФЭ: конъюнктор, дизъюнктор, инвертор.

Пример:

СФЭ:

1.любой полис, которому приписана булева переменная, является СФЭ

2.совместное рассмотрение 2­х схем их ФЭ является тоже СФЭ.

Говорят, что СФЭ реализует булеву функцию f, если существует полюс схемы, которому приписана функция f .

L(S) ­ кол­во функциональных элементов в схеме.

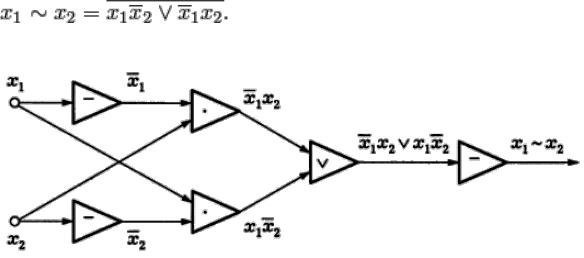
22. Реализация сумматора в классе классе схем из функциональных элементов.

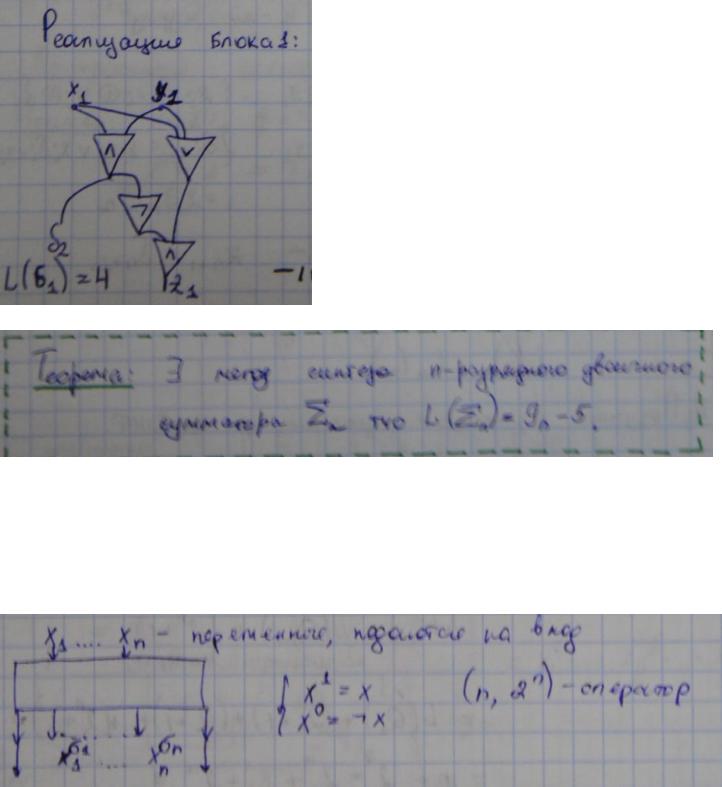
23. Реализация дешифратора классе схем из функциональных элементов .

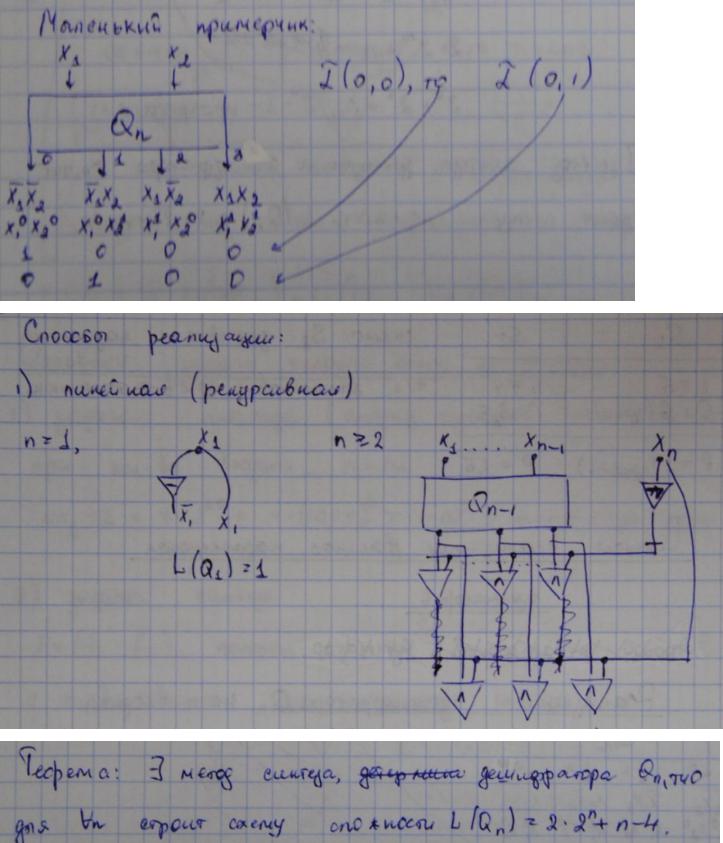
24. Универсальные методы синтеза классе схем из функциональных элементов.

Синтез ­ построение СФЭ, которая реализует функцию f.

1. Метод А1: представление функции в виде СДНФ

2. Метод А2: основан на использовании дешифратора

3. Мощностной метод Шеннона