3Случайные Величины

	-10	10
	0,5	0,5

Какое из орудий стреляет лучше?

Решение. Найдём математические ожидания попаданий каждой из зениток:

, .

Математические ожидания одинаковые, но кучность стрельбы первого орудия выше (отклонение от центра меньше). Значит, лучшим следует признать первое орудие. ◄

Как показывает пример, среднее арифметическое отклонений может быть равным нулю. Это объясняется тем, что значения имеют противоположные знаки и взаимно погашаются при нахождении среднего арифметического.

Найдем математическое ожидание отклонения:

,

то есть, математическое ожидание отклонения равно нулю. Поэтому отклонение нельзя принимать за меру рассеяния значений случайной величины вокруг центра распределения. Обычно используют модули отклонений или их квадраты.

Определение 7.2. Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения:

.

Преобразуем последнюю формулу:

.

Таким образом, дисперсия случайной величины равна разности математического ожидания квадрата этой величины и квадрата ее математического ожидания:

.

Эту формулу удобно применять в практических вычислениях.

Если СВ дискретная с законом распределения , , то СВ имеет закон распределения:

, , .

По определению математического ожидания получаем ещё одну формулу

для вычисления дисперсии ДСВ с конечным числом значений.

Если ДСВ принимает счётное множество значений, то ее дисперсия находится по формуле:

при условии, что ряд сходится, .

Дисперсия НСВ , принимающей значения из отрезка , определяется формулой

,

где – плотность распределения вероятности этой величины.

В этом же случае можно использовать другую формулу:

.

Докажите ее самостоятельно.

В общем случае дисперсия НСВ определяется формулой:

,

если интеграл сходится;

или

.

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю:

.

Доказательство. По определению и свойствам математического ожидания получаем:

.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

Доказательство. По определению и свойствам математического ожидания получаем:

.

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

.

Доказательство.

.

Это свойство справедливо для любого числа попарно-независимых случайных величин.

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

.

Доказательство. Для доказательства применим второе и третье свойства дисперсии:

.

Среднее квадратическое отклонение. Размерность дисперсии равна квадрату размерности случайной величины, поэтому в случае, когда желательно получить оценку рассеяния случайной величины в тех же единицах, что и сама величина, находят корень квадратный из дисперсии.

Определение 7.3. Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии:

.

Таким образом, зная введённые две числовые характеристики – математическое ожидание и среднее квадратическое отклонение – получаем ориентировочное представление о пределах возможных значений случайной величины.

Мода и медиана. Математическое ожидание характеризует положение случайной величины – «центр» закона распределения. Существуют еще две числовые характеристики случайной величины такого рода – медиана и мода .

Определение 7.4. Модой ДСВ называется значение , соответствующее её наиболее вероятному значению, а модой НСВ – значение, при котором плотность распределения вероятности максимальна.

На рис. 2 и 3 указаны значения моды для ДСВ и НСВ . Вообще случайные величины могут иметь несколько модальных значений.

О пределение 7.5. Медианой случайной величины называется такое её значение , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , то есть

.

С геометрической точки зрения медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 4). В случае симметричности кривой распределения медиана совпадает с модой и математическим ожиданием (рис. 5).

Медиана является корнем уравнения . Математического ожидания у случайной величины может и не быть, а медиана существует всегда. Медианой необязательно является одна точка. Если на , то любая точка этого интервала является медианой.

С оотношения между математическим ожиданием, медианой и модой для некоторых плотностей распределения вероятностей показаны на рис. 6. Математическое ожидание «чувствительно» к «хвостам» закона распределения, медиана менее чувствительна к ним, а на моду крайние значения вообще не влияют.

Моменты распределения случайных величин. Обобщением основных числовых характеристик случайных величин, описывающих центр распределения (математического ожидания, моды, медианы) и рассеивание (дисперсии и среднего квадратического отклонения), является понятие моментов. Их ценное свойство состоит в том, что моменты более низкого порядка несут больше информации о случайной величине, чем моменты высокого порядка.

Определение 7.6. Начальным моментом -того порядка СВ называется математическое ожидание -той степени этой величины, то есть

.

Для ДСВ с возможными значениями , …, , … и с соответствующими вероятностями , …, , … имеем:

при условии, что этот ряд сходится абсолютно.

Для НСВ с плотностью вероятности :

,

если этот интеграл сходится абсолютно.

Запишем формулы, выражающие начальные моменты -того порядка при , для дискретной и непрерывной случайных величин:

, ;

, ;

, .

Определение 7.7. Центральным моментом -того порядка СВ называется математическое ожидание -той степени отклонения этой величины от ее математического ожидания, то есть

.

Для ДСВ с возможными значениями , …, , … и с соответствующими вероятностями , …, , … имеем:

при условии, что ряд сходится абсолютно.

Для НСВ с плотностью вероятности :

,

если этот интеграл сходится абсолютно.

Запишем формулы, выражающие центральные моменты -того порядка при , для дискретной и непрерывной случайных величин:

, ;

;

, .

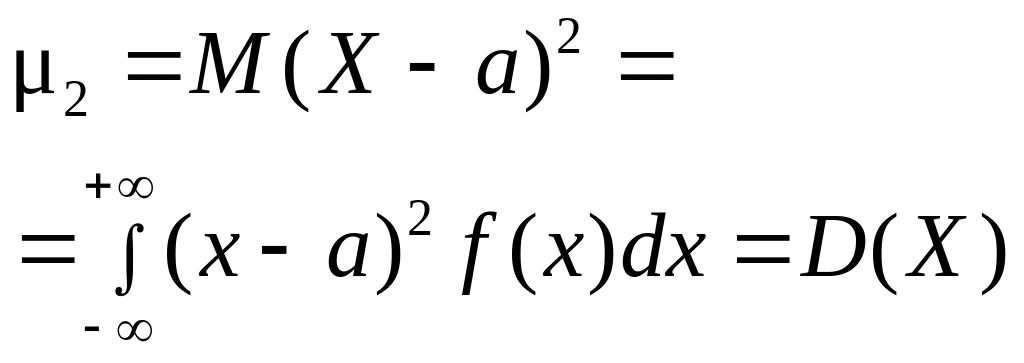Центральный момент порядка можно выразить через начальные моменты:

.

.

Аналогично выводится формула

.

Центральный момент третьего порядка характеризует асимметрию («скошенность») распределения случайной величины. Для получения безразмерной характеристики делят на .

Отношение называется коэффициентом асимметрии. Если распределение симметрично относительно математического ожидания, то все моменты нечётного порядка равны нулю.

Е сли кривая распределения непрерывной случайной величины такова, что справа от моды расположена её «длинная часть», а слева – «короткая часть», то коэффициент асимметрии положителен. Коэффициент асимметрии отрицателен, когда «длинная часть» кривой распределения расположена слева от моды.

На рис. 7 показаны кривые распределения с положительной и отрицательной асимметриями.

Четвёртый центральный момент является характеристикой «крутости», то есть островершинности или плосковершинности распределения. Эти свойства описываются с помощью эксцесса, то есть величины

.

Ч исло 3 вычитается из отношения потому, что все распределения сравниваются с нормальным распределением (его рассмотрим позже), для него . Кривые, более островершинные по сравнению с нормальной, обладают положительным эксцессом. Кривые более плосковершинные – отрицательным эксцессом (рис. 8).

1 Плотность вероятности ещё называют дифференциальной функцией распределения случайной величины.

2 Функцию распределения ещё называют интегральной функцией распределения случайной величины.

66