
MetodUkazначерт
.pdf-образующая и направляющие поверхности;
-линейчатая и нелинейчатая поверхности;
-определитель поверхности;
-задание поверхности на чертеже;
-очерк поверхности;
-принадлежность точки и линии поверхности;
-нахождение недостающей проекции точки, принадлежащей поверхности.
Опираясь на знания указанных положений, студент должен выполнить на чертеже следующие действия:
-провести линию, принадлежащую заданной поверхности;
-на поверхности задать ряд ее образующих;
-определить, принадлежит ли точка поверхности;
-зная одну проекцию точки, принадлежащей поверхности, найти ее вторую проекцию.
2.2.2.Рекомендации к решению задачи и выполнению построений
Во всех случаях задана линейчатая поверхность.
Точка находится на поверхности, если она принадлежит какой-либо линии этой поверхности.
Для решения задачи по нахождению недостающей проекции точки принадлежащей поверхности, через заданную проекцию точки проводим одноименную проекцию линии, принадлежащей поверхности, Строим вторую проекцию проведенной линии и на ней находим вторую проекцию точки.
Желательно через точку на поверхности проводить прямую (образующую) или окружность.
На поверхности однополостного гиперболоида вращения через точку всегда можно провести окружность (параллель), принадлежащую плоскости, перпендикулярной оси вращения.
При заданном положении однополостного гиперболоида вращения относительно плоскостей проекций окружность (параллель) на фронтальную плоскость проекций проецируется
вотрезок прямой, параллельный оси проекций х, а на горизонтальную плоскость проекций –
вокружность.
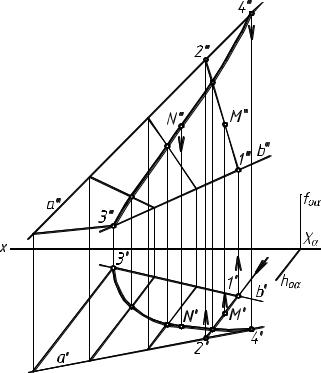
Проведение через заданные точки окружностей, принадлежащих однополостному гиперболоиду вращения, не представляет сложности, поэтому мы не приводим чертеж этих построений (нужно только обратить внимание на возможность двух вариантов решения задач). На поверхности косой плоскости (рис. 6) через горизонтальную проекцию точки М ( М ') можно провести горизонтальную проекцию образующей (прямой 1 2), так как все образующие параллельны плоскости параллелизма α, занимающей горизонтально проецирующее положение. Горизонтальная проекция образующей 1 2 (1' 2 ') параллельна горизонтальному
следу hoα .
Через фронтальную проекцию точки N ( N") нельзя провести фронтальную проекцию образующей, так как мы не знаем ее направления. Приходится проводить фронтальную проекцию кривой линии (хотя она может проецироваться на фронтальную плоскость проекций в прямую). Для нахождения горизонтальной проекции проведенной линии на поверхности косой плоскости проводим ряд образующих (сначала проводим их горизонтальные проекции) и находим точки пересечения образующих с проведенной линией. Строим горизонтальные проекции этих точек, через которые пройдет горизонтальная проекция проведенной линии. Этой линии принадлежит точка N .
На поверхности косого геликоида через горизонтальную проекцию точки М (М') можно провести горизонтальную проекцию образующей (все образующие пересекают ось винтовой поверхности). Фронтальную проекцию точки пересечения проведенной образующей с осью винтовой линии найти легко, так как известна разность координат z, крайних точек этих образующих (все образующие имеют одинаковый угол наклона к горизонтальной плоскости
11
проекций).
Рис. 6 |
Через фронтальную проекция точки N ( N") нельзя провести фронтальную проекцию образующей, так как мы не знаем ее направление. Приходится проводить фронтальную проекцию кривой линии (хотя она может проецироваться в прямую), как и для поверхности косой плоскости (см. рис. 6).
2.2.3.Вопросы для подготовки к защите
1.Какая поверхность задана на чертеже?
2.Какая линия является образующей поверхности?
3.Какие линии являются направляющими поверхности?
4.Как найти недостающую проекцию точки, принадлежащей поверхности?
2.3.Способы преобразования чертежа
2.3.1.Подготовка к решению задачи
Для всех вариантов по заданному чертежу пирамиды надо, используя способы преобразования чертежа, определить: высоту пирамиды, истинный вид основания, угол наклона одного из ребер к основанию, величину двугранного угла между одной из граней и основанием.
Для решения указанных задач необходимо знать следующие фундаментальные положения начертательной геометрии:
-сущность способа замены плоскостей проекций;
-сущность способа вращения вокруг линий уровня. Кроме того, студент должен уметь:
-преобразовать чертеж так, чтобы заданные геометрические фигуры заняли частные положения относительно плоскостей проекций (параллельно или перпендикулярно);
-определить величину двугранного угла;
12
- определить величину угла между прямой и плоскостью.
Опираясь на указанные знания, студенту необходимо уметь выполнить на чертеже следующие действия:
-заменой плоскостей проекций преобразовать чертеж так, чтобы прямая стала параллельной (перпендикулярной) новой плоскости проекций;
-заменой плоскостей проекций преобразовать чертеж так, чтобы плоскость стала перпендикулярной новой плоскости проекций;
-повернуть плоскую фигуру вокруг линии уровня, чтобы она стала параллельной плоскости проекций,
-провести проекции прямой, перпендикулярной заданной плоскости.
2.3.2. Рекомендации к решению задачи и выполнению построений
Задание геометрических фигур в частных положениях относительно плоскостей проекций (параллельно или перпендикулярно им) значительно облегчает решение задач. Этого можно достигнуть, используя способы преобразования чертежа, не изменяя взаимного положения заданных фигур. В курсе начертательной геометрии изучают два способа преобразования чертежа: способ замены плоскостей проекций и способ вращения. Сущность способа замены плоскостей проекций заключается в том, что заданные геометрические фигуры остаются неподвижными, а плоскости проекций подвижны. При этом, имея систему двух взаимно перпендикулярных плоскостей проекций, заменяют одну из плоскостей, а вторую оставляют. Новая плоскость проекций должна быть перпендикулярна оставшейся. Такие замены можно проводить последовательно необходимое число раз,
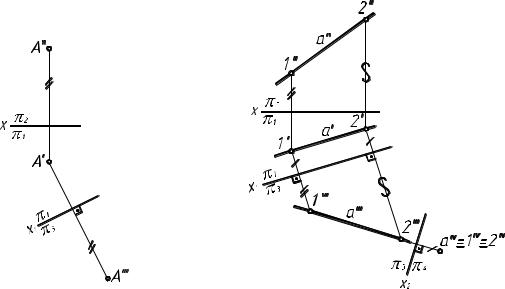
На рис.7 даны две проекции точки А. Заменяем плоскость проекций π2 на π3, оставляя неизменной π1. Находим А''', исходя из неизменности координаты z точки A.
Рассмотрим примеры использования способа замены плоскостей проекций для преобразования чертежа таким образом, чтобы прямые и плоскости заняли частные положения относительно новых выбранных плоскостей проекций.
Рис.7 |
Рис.8 |
Чтобы прямая заняла положение, параллельное новой плоскости проекций (рис.8), выбираем ось х1 параллельно а' и строим проекции на плоскость π3 двух точек, принадлежащих
13
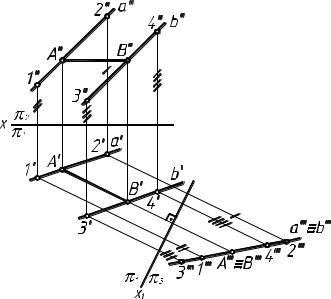
прямой. Теперь можно выбрать плоскость проекций π4, относительно которой прямая а будет перпендикулярна. Для этого ось проекций х2 должна быть перпендикулярна а'''.
Внимательно изучите данный чертеж. Одной из важных характеристик решения задач начертательной геометрии является рациональность. Запомните, сколько замен плоскостей проекций необходимо произвести, чтобы прямую общего положения перевести в положение, параллельное (перпендикулярное) новой плоскости проекций.
Перевод плоскости из общего положения в проецирующее может быть облегчен с помощью какой-либо линии уровня (горизонтали или фронтали), принадлежащей плоскости. На рис. 9 плоскость общего положения задана двумя параллельными прямыми. Из курса геометрии известно, что плоскость, перпендикулярная другой плоскости, содержит перпендикуляр к этой плоскости. Иными словами, чтобы плоскость стала перпендикулярна новой плоскости проекций, надо поставить одну из прямых, принадлежащих плоскости, в положение, перпендикулярное новой плоскости проекций. За такую прямую выбираем АВ, являющуюся горизонталью плоскости. Можно было использовать и прямую общего положения, но, как видно из предыдущего примера, она переводится в проецирующее положение большим числом замен плоскостей проекций. Все дальнейшие построения видны на чертеже.
Рис.9
Второй заменой можно поставить заданную плоскость параллельно новой плоскости проекций π4 (на чертеже не показано, так какэтим практически пользоваться не будем).
Сущность способа вращения вокруг прямой, параллельной плоскости проекций, заключается в том, что плоскую фигуру поворачивают вокруг ее горизонтали или фронтали до положения, когда плоская фигура станет параллельной соответствующей плоскости проекций.
На рис. 10 плоскость задана прямой h (горизонталью) и точкой А.
14
Рис.10
Вращаем плоскость вокруг горизонтали h, которая при этом остается на месте. Для нахождения положения плоскости после поворота достаточно повернуть точку А. Точка А перемещается в плоскости γ, перпендикулярной оси вращения (горизонтали h). Точка перемещается по окружности с центром в точке С, являющейся точкой пересечения оси вращения h с плоскостью γ . Радиус окружности равен расстоянию от вращаемой точки А до центра С (отрезок АС). После поворота отрезок АС будет проецироваться на π1 без искажения. Находим его величину построением прямоугольного треугольника и откладываем от точки С. Таким образом, плоскость стала параллельной плоскости проекций и ее положение задано точкой А(А'1) и прямой h ( h'1 ) .
Как уже говорилось, по условию задачи требуется определить:
а) высоту пирамиды; б) истинный вид основания АВС;
в) угол между плоскостями (гранью SAB и основанием АВС); г) угол между ребром SA и основанием ABC .
Высота пирамиды - это перпендикуляр, опущенный из вершины S на основание АВС . Для определения высоты надо преобразовать чертеж так, чтобы основание АВС стало перпендикулярным новой плоскости проекций. Тогда на него легко опустить перпендикуляр, и он будет параллелен новой плоскости проекций, т.е. будет проецироваться на нее без искажения (рис. 11).
15
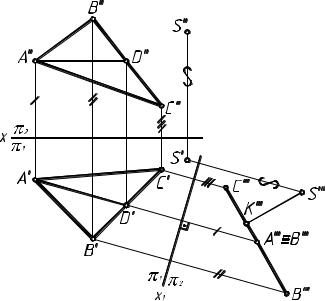
Рис.11
Для определения истинного вида основания АВС его надо повернуть вокруг горизонтали или фронтали до положения параллельного горизонтальной или фронтальной плоскости проекций (см. рис. 10).
Двугранный угол между плоскостями определяют величиной острого угла между прямыми, перпендикулярными прямой пересечения этих плоскостей (ребру двугранного угла) и принадлежащими заданным плоскостям. Если плоскость, заданная этими прямыми, будет параллельна какой-либо плоскости проекций, то угол между ними будет проецироваться на данную плоскость проекций без искажения. Это будет иметь место в случае, когда ребро двугранного угла будет перпендикулярно плоскости проекций. Поэтому необходимо преобразовать чертеж так, чтобы прямая АВ заняла положение перпендикулярное новой плоскости проекций и найти новые проекции грани SAB и основания ABC. Они в этом случае будут проецироваться на эту плоскость проекций в прямые, так как будут перпендикулярны плоскости проекций (см. рис. 8).
Угол между прямой и плоскостью определяют величиной острого угла между прямой и ее проекцией на данную плоскость.
Для нахождения величины угла между ребром SА и основанием ABC нет необходимости проецировать ребро SA на плоскость АВС.
На рис. 12 угол φ° определяет величину угла между прямой АВ и плоскостью α. Но если из произвольной точки прямой А В (в нашем примере - из точки В) провести прямую, перпендикулярную плоскости α (именно провести, а не опустить перпендикуляр, т.е. не находить пересечение перпендикуляра с плоскостью), то угол между заданной прямой и проведенным перпендикуляром (угол γ ° ) будет равен 90°- φ°. Поэтому через любую точку ребра SA надо провести прямую, перпендикулярную основанию АВС. Получим две пересекающиеся прямые: ребро SА и проведенный перпендикуляр. Плоскость, заданную этими пересекающимися прямыми, вращаем вокруг горизонтали или фронтали и определяем величину угла γ °. Теперь надо графически из 90° вычесть величину угла γ ° для определения величины угла φ°
(рис. 13).
16
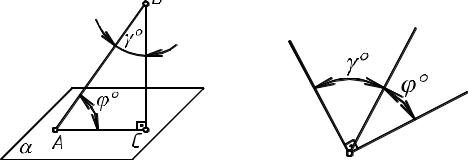
Рис.12. |
Рис.13 |
2.3.3.Вопросы для подготовки к защите
1.Для чего применяют способы преобразования чертежа?
2.В чем сущность способа замены плоскостей проекций?
3.В чем сущность способа вращения вокруг линий уровня?
4.Какой круг задач можно решать, используя способ вращения вокруг линий уровня?
5.Какой величиной определяют угол между прямой и плоскостью, как ее определяли в данной задаче?
6.Какой величиной определяют двугранный угол между плоскостями, как ее определяли в данной задаче?
2.4.Построение линий пересечения поверхностей
2.4.1, Подготовка к решению задачи
Задача по построению линии пересечения поверхностей может считаться наиболее сложной и трудоемкой из всех задач домашнего задания, так как при ее решении кроме знания материала, непосредственно относящегося к теме задачи, потребуется и умение использовать материал практически всего курса начертательной геометрии, изученный к данному моменту (темы: точка, прямая, плоскость, поверхности,, способы преобразования чертежа). К решению задачи не следует приступать раньше, чем будет освоен материал всех предыдущих разделов курса.
Необходимость определения большого числа промежуточных точек для построения проекций линий пересечения заданных поверхностей требует от студента высокой точности
иаккуратности самих построений, отработанной техники черчения. Очень часто погрешность построения приводит я грубым смысловым ошибкам. При выполнении этой задачи следует особенное внимание уделить точности и тщательности построений.
Кроме того, построение проекций линий пересечения поверхностей требует учета большого числа признаков, факторов и особенностей проецирования как линий в целом, так
иотдельных их участков. Поэтому при решении задачи следует особенно тщательно соблюдать рекомендуемый ниже порядок действий и этапность решения задачи.
Подготовку к решению задачи следует начать с проработки и повторения следующих основных положений:
1.Понятие о принципе построения линии пересечения поверхностей на чертеже и составление алгоритма решения данной задачи.
2.Построение линии пересечения поверхностей для случая, когда хотя бы одна из них занимает проецирующее положение относительно какой-либо плоскости проекций.
3.Принцип выбора вспомогательных секущих поверхностей при решении задачи по общему алгоритму для случая, когда ни одна из пересекающихся поверхностей не занимает проецирующего положения относительно какой-либо плоскости проекций.
17
4.Решение задачи с помощью вспомогательных плоскостей,
5.Способ вспомогательных концентрических сфер (в каких случаях его применяют).
6.Способ вспомогательных эксцентрических сфер (в каких случаях его применяют).
7.Особые случаи пересечения поверхностей второго порядка.
Успех решения каждой конкретной задачи в значительной мере зависит от того, насколько хорошо студент владеет материалом по теме "Поверхности". Способ их образования. Точка и линия на поверхности. Целесообразно повторить этот материал, обращая особое внимание на следующие вопросы:
1.Как определить, что точка принадлежит поверхности?
2.Какие поверхности являются носителями прямых линий, окружностей?
3.Какое положение относительно плоскостей проекций занимают прямые линии, окружности, принадлежащие этим поверхностям?
4.Как проецируются эти прямые линии, окружности при различном расположении поверхностей относительно плоскостей проекций?
5.Сколько, семейств окружностей существует на поверхности тора? Как они расположены?
Вкаждом индивидуальном задании на построение линии пересечения поверхностей задана монолитная (не полая) фигура, ограниченная комбинациями простейших поверхностей.
Вкаждом задании необходимо построить несколько линий пересечения (минимум две). Для правильного и полного решения задачи ее следует расчленить на ряд элементарных составляющих, выделяя пары пересекающихся поверхностей. Для каждой пары поверхностей необходимо решить задачу отдельно, каждый раз строго выполняя все этапы.
Искомая линия пересечения есть объединение всех ее участков, построенных при решении элементарных задач.
Следует иметь в виду, что каждая из выделенных поверхностей существует лишь до линии ее пересечения с другой поверхностью. Поверхности не являются тонкостенными оболочками, а лишь ограничивают монолитную фигуру, не имеющую внутренних полостей.
2.4.2.Указания к решению задачи и выполнение построения
1. Анализ условия задачи:
а) определяем вид (название) пересекающихся поверхностей: (линейчатая, вращения, второго порядка и др.);
б) выделяем поверхности, занимающие проецирующее положение относительно какой-либо плоскости проекций;
в) устанавливаем, какие простейшие линии могут быть проведены на каждой из пересекающихся поверхностей, как эти линиирасположены и как они проецируются на каждую из плоскостей проекций;
г) выявляем особенности взаимного расположения пересекающихся поверхностей: взаимное положение их осей, наличие общей плоскости симметрии и ее положение относительно плоскостей проекций, наличие точек касания, общего плоского сечения для поверхностей второго порядка и т.п.
2. Определение типа задачи:
а) хотя бы одна из пересекающихся поверхностей занимает проецирующее положение относительно какой-либо плоскости проекций;
б) ни одна из пересекающихся поверхностей не занимает проецирующего положения относительно плоскостей проекций;
в) имеется возможность использовать теоремы о частных случаях пересечения поверхностей второго порядка.
3. Построение особых точек кривой пересечения, к которым, относятся:
18
а) точки с максимальным и минимальным значениями координат x, y и z - высшая, низшая, крайняя правая, крайняя левая, крайняя передняя, крайняя задняя;
б) точки, принадлежащие очеркам проекций поверхностей, точки перегиба кривой, среди которых точки - границы видимости кривой при проецировании на каждую плоскость проекций.
4.Построение промежуточных точек кривой пересечения.
5.Построение проекций кривой пересечения поверхностей, выделение видимых и невидимых участков линии пересечения.
6.Определение протяженности очерков проекций поверхностей и их видимости.
7.Обводка чертежа.
Решение задачи, когда хотя бы одна из пересекающихся поверхностей занимает проецирующее положение относительно какой-либо плоскостей проекций, базируется на следующих положениях:
Правило 1. Если хотя бы одна из пересекающихся поверхностей занимает проецирующее положение относительно какой-либо плоскости проекций, то на чертеже присутствует одна из проекций линии пересечения. Она принадлежит (совпадает) следу поверхности на эту плоскость проекций. Вторую проекцию этой линии строят из условия ее принадлежности другой, не проецирующей поверхности.
Если эта проекция линиипересечения представляет собой лекальную кривую, то задача сводится к построению недостающих проекций ряда точек, принадлежащих линии пересечения и соединению их плавной кривой линией.
Правило 2. Если обе пересекающиеся поверхности занимают проецирующее положение относительно разных плоскостей проекций, то на чертеже присутствуют обе проекции линии пересечения. Их надо лишь правильно указать (обозначить). Никаких построений в этом случае выполнять не требуется.
Правило 3. Если обе пересекающиеся поверхности занимают проецирующее положение относительно одной и той же плоскости проекций, то линия их пересечения есть прямая (несколько прямых), проецирующая по отношению к той же плоскости проекций.
Если ни одна из пересекающихся поверхностей не занимает проецирующего положения относительно плоскостей проекций, используем вспомогательные плоскости или сферы (концентрические или эксцентрические). Вспомогательную поверхность выберем таким образом, чтобы она пересекала исходные поверхности по возможно более простым и удобно расположённым относительно плоскостей проекций линиям для сокращения числа промежуточных построений и повышения их точности или чтобы линия пересечения вспомогательной поверхности с заданными проецировалась в виде простых линий (прямых или окружностей). Всегда следует избегать построения промежуточных лекальных кривых, если есть возможность получить на поверхности окружности и, особенно, прямые линии.
Рассмотрим решение задачи на примере (рис. 14). Необходимо построить линии пересечения поверхностей, отражающие характер, содержание и уровень сложности задач домашнего задания.
19
Рис.14
Общий анализ условия задачи говорит о том, что поверхность заданной фигуры ограничена сферой (О), поверхностью прямого кругового цилиндра (Ц), прямого кругового конуса (К), передней фронтальной плоскостью α, задней фронтальной плоскостью β, горизонтальной плоскостью основания γ.
На поверхности фигуры надлежит построить линию пересечения, включающую следующие составляющие:
а) линию пересечения конической поверхности и фронтальной плоскости α;
б) линию пересечения сферы и фронтальной плоскости α; в) линию пересечения цилиндрической поверхности и горизонтальной плоскости γ ; г) линию пересечения цилиндрической поверхности и сферы;
д) линию пересечения конической поверхности и сферы.
Решим последовательно эти задачи, начиная с тех случаев, в которых хотя бы одна из пересекающихся поверхностей занимает проецирующее положение относительно какойлибо плоскости проекций. Как известно, в этих случаях решение задачи значительно упрощается, так как нет необходимости использовать общий алгоритм, вводя вспомогательные поверхности.
Пересечение конической поверхности и плоскости (рис. 15). Плоскость α перпендикулярна горизонтальной плоскости проекций и параллельна фронтальной плоскости проекций, а также параллельна двум образующим конической поверхности. Линия пересечения - гипербола. Ее горизонтальная проекция - отрезок прямой, совпадающий с горизонтальным следом плоскости (см. правило 1). На фронтальную плоскость проекций гипербола проецируется без искажения.
20
