
668
.pdf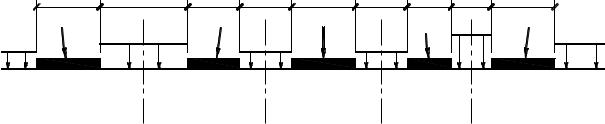
2.2.6. Предельное давление на основание произвольного числа штампов
Последовательность краевых задач, рассмотренная в предыдущем пункте и показанная на рис. 2.35, позволяет перейти к наиболее общей из задач о взаимном влиянии − задаче о несущей способности основания n штампов шириной bi, отстоящих друг от друга на расстоянии ai, при действии в интервалах между штампами различных пригрузок qi. Граничные условия к этой задаче показаны на рис. 2.37. Каждая из линий Oizi проходит через середину соответствующего отрезка между штампами.
|
b1 |
|
a1 |
b2 |
a2 |
b3 |
a3 |
b i |
ai |
bn |
|
|
|
Pu,1 |
q |
|
Pu,2 |
|
P |
|
P |
q i |
Pu, n |
q |
|
|
|
|
u,3 |
|
|
|
||||||
q |
1 |
q2 |
|
q3 |
u, i |
|
n |
|||||
0 |
|
|
|
|
|
|
|
|||||
|
|
O1 |
|
O2 |
|
O3 |
|
Oi |
|
|
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
z1 |
|
z2 |
|
z3 |
|
z i |
|
|
|
|
Рис. 2.37. Граничные условия к задаче о несущей способности произвольного количества штампов
Построение, показанное на рис. 2.35, позволяет определить для данной схемы условия вида (2.50) на всех линиях Oizi:
x = x , α = − π + (i − j)π, |
(2.51) |
i |
2 |
|
где xi − координата оси Oizi в глобальной системе координат xOz, в качестве которой может быть принята, например, любая из систем xOizi; j − некоторое наперед заданное целое число.
Итак, для того чтобы определить непрерывное поле статически безопасных предельных напряжений в задаче о произвольном количестве штампов, необходимо построить решение для (n − 2) расчетных схем, заключенных между осями Oizi, и Oi−1zi−1, и для двух крайних штампов − слева от оси O1z1 и справа от оси
On−1zn−1.
Последовательность краевых задач в решении для крайних штампов совпадает с решением задачи о несущей способности основания двух штампов. Компоновка зон предельного равнове-
143
сия, которую здесь следует использовать, дана на рис. 2.28. Для нахождения величины предельной нагрузки следует использовать графики рис. 2.33 с учетом выводов и замечаний, сделанных по задаче о двух штампах.
При построении решения для i-го штампа, находящегося между осями Oizi, и Oi−1zi−1, выделим два основных расчетных случая.
В первом случае слева и справа от штампа граничные условия заданы симметрично:
qi−1 = qi , ai−1 = ai . |
(2.52) |
В качестве примера может быть рассмотрен 3-й штамп на рис. 2.37, поскольку, как видно из приведенной схемы, q2 = q3, a2 = a3. Для таких штампов решение от оси Oi−1zi−1 и оси Oizi будет строиться одинаково, и поле предельных напряжений станет симметричным относительно вертикальной оси, проходящей через середину i-го штампа. Таким образом, при задании граничных условий вида (2.52) решение в области, находящейся между осями Oi−1zi−1 и Oizi, совпадает с рассмотренным ранее решением задачи о предельном давлении на основание бесконечного ряда штампов. Последовательность краевых задач, которую здесь следует использовать, показана на рис. 2.24. Предельная нагрузка может быть найдена с помощью графиков на рис. 2.26.
Если на участках границы основания, свободных от штампов, всюду задана равномерная пригрузка q, все штампы имеют одинаковую ширину b и отстоят друг от друга на одинаковом расстоянии a, то несущая способность основания данной системы штампов может быть рассчитана по формуле
Pu = 2Pu,êð + (n − 2)Pu,ñð ,
где Pu,кр и Pu,ср − вертикальные равнодействующие силы предельного давления на крайний и средний штампы соответственно, n − общее число штампов.
Ко второму расчетному случаю ведет невыполнение какогото одного или сразу обоих условий (2.52). Последовательность краевых задач, составляющая решение в этом случае, дана на рис. 2.38.
144

Рис. 2.38. Последовательность краевых задач в основании i-го штампа
при несимметричном задании граничных условий
145
По существу, порядок численного решения здесь совпадает с рассмотренным в задаче о бесконечном ряде штампов (см. рис. 2.24). Однако, как видно из рис. 2.38, построение областей предельного равновесия от оси Oi−1zi−1 и от оси Oizi, будет несимметричным, и возникает необходимость сопряжения зон предельного напряженного состояния при интегрировании канонической системы уравнений справа и слева от штампа. Сама процедура сопряжения была рассмотрена выше на примере двух штампов (см. рис. 2.29).
На рис. 2.39 показан пример сетки линии скольжения для следующих исходных данных: ширина штампа b = 1 м, расстояние до ближайшего штампа слева ai−1 = 0,8 м, расстояние до ближайшего штампа справа ai = 1,4 м, угол внутреннего трения ϕ = 30°, удельное сцепление c = 1 кПа, удельный вес грунта γ = 20 кН/м3, пригрузка слева qi−1 = 5 кПа, пригрузка справа qi−1 = 3 кПа. Здесь же дано очертание эпюр нормальных и касательных давлений по подошве штампа. Равнодействующая предельного давления на штамп шириной 1 м составила 380 кН.
Более детальный анализ этого решения по образцу предыдущих здесь не приводится из-за большого числа входящих параметров. Однако ясно, что результаты решения данной задачи во многом будут коррелировать с выводами, сделанными ранее. В частности, очевидно, что при сближении штампов несущая способность будет увеличиваться, эффект взаимного влияния будет проявляться сильнее с ростом угла внутреннего трения и т.д.
Таким образом, решение задачи о взаимном влиянии произвольного количества штампов различной ширины на несущую способность горизонтального грунтового основания будет сводиться к численному интегрированию канонической системы уравнений ТПРГ в рамках трех схем, показанных на рис. 2.24, 2.28 и 2.38.
146
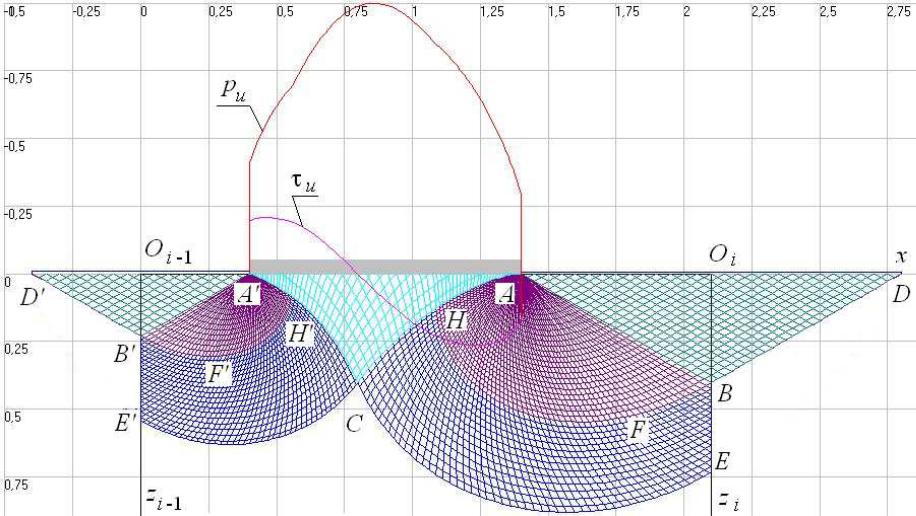
Рис. 2.39. Сетка линий скольжения в основании i-го штампа
147
§ 2.3. Устойчивость откосов и склонов |
|
|
||||
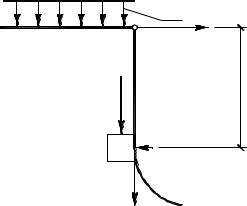
2.3.1. Предельная высота вертикального откоса |
|
|||||
Рассмотрение проблемы устойчивости откосов и склонов |
||||||
начнем с наиболее простой задачи определения предельной вы- |
||||||
соты вертикального откоса. Этот вопрос имеет значение как в |
||||||
теоретическом отношении, так и в строительстве, особенно при |
||||||
производстве работ. |
|
|
|
|
||
Из практического опыта из- |
|
p |
|
|||
вестно, что грунт в состоянии |
O |
x |
|
|||
держать весьма крутые и даже |
|
|||||
вертикальные |
откосы. |
Однако |
σ1 = γz + p |
h |
|
|
также понятно, что высота такого |
пр |
|||||
|
|
|||||
откоса ограничена − она зависит |
|
σ3= 0 |
|
|||
от прочности грунта и внешнего |
|
|
||||
|
|
|
||||
давления на бровке откоса. |
|
|
|
|||
Рассмотрим |
схему, |
показан- |
z |
|
|
|
ную на рис. 2.40. Грунт характери- |
|
|
||||
|
|
|
||||
зуется параметрами прочности ϕ и |
Рис. 2.40. Схема к определению |
|||||
c, удельным весом γ. Для общно- |
высоты вертикального откоса |
|||||
сти предположим, что на бровке |
|
|
|
|||
действует нагрузка интенсивностью p. Предельную высоту вер- |
||||||
тикального откоса обозначим через hпр. Далее, прочности грунта |
||||||
оказывается недостаточно, чтобы сохранять вертикальное очер- |
||||||
тание склона, и намечается тенденция к его выполаживанию. Та- |
||||||
ким образом, на глубине hпр откос находится в предельном |
||||||
напряженном состоянии. |
|
|
|
|
||
Поскольку вертикальная граница откоса принимается сво- |
||||||
бодной от напряжений, в том числе и касательных, то напряже- |
||||||
ния σz и σ x на ней главные. Тогда из условий равновесия верхней |
||||||
части грунтового массива мощностью hпр непосредственно сле- |
||||||
дует: |
σz = σ1 = γhï ð + p, |
|
|
|||
|
|
|
||||
а из граничных условий вдоль Oz: |
|
|
|
|||
σx = σ3 = 0.
Подставим эти выражения в закон Кулона–Мора в главных напряжениях (1.15):
γhï ð + p + 0 = (γhï ð + p + 0 + 2ñ ctgϕ)sin ϕ,
148
откуда и выразим предельную высоту вертикального откоса:
|
|
1 2ccosϕ |
|
|
|||
hï ð |
= |
|
|
|
− p . |
(2.53) |
|
γ |
1− sin ϕ |
||||||
|
|
|
|
|
|||
Если на бровке внешняя нагрузка p = 0 отсутствует, то выражение (2.53) можно переписать в виде:
h |
= |
2c |
|
|
cosϕ |
. |
(2.54) |
|
|
|
|||||
ï ð |
|
γ |
1 |
− sin ϕ |
|
||
|
|
|
|||||
Из (2.54) нетрудно получить высоту вертикального непригруженного откоса идеально-связного грунта:
2c
hï ð = γ .
Для идеально-сыпучего эта величина равна нулю, что является очевидным фактом, поскольку несвязанные друг с другом песчаные частицы в принципе не в состоянии держать вертикальный откос.
2.3.2. Предельное давление на невесомый откос
Далее обратимся к задаче о предельном давлении на невесомый откос. Следует подчеркнуть, что собственный вес грунта, слагающего тот или иной склон, как правило, относится к основным факторам, влияющим на устойчивость склона, и с практической точки зрения принимаемая идеализация может быть оправдана только если собственный вес откоса считать незначительным по сравнению с ожидаемой на него нагрузкой. Данная задача является одной из немногих среди задач устойчивости откосов и склонов, которая может быть решена аналитически в рамках статического метода теории предельного равновесия, а результаты решения частично будут использованы в дальнейшем.
Расчетная схема этой задачи показана на рис. 2.41. На бровке OA откоса AD, составляющего с горизонталью угол β, действует равномерное предельное давление pu. Откос AD свободен от пригрузки. Требуется определить предельную нагрузку pu.
Опираясь на рассмотренное в § 2.1 решение задачи Прандтля для невесомой среды, в приоткосной части можно выделить три зоны: максимального ABD, переходного ABC и минимального OAC напряженных состояний грунта.
149
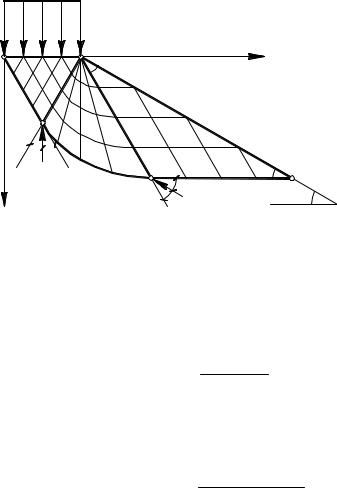
Область ABD в системе координат xOz расположена иначе, чем зоны максимального напряженного состояния в рассмотренных нами ранее решениях. Вначале определим значение парамет-
|
|
pu |
|
|
|
|
|
ра α на границе AD. По- |
|||
|
|
|
|
|
|
|
скольку |
на свободной |
|||
O |
|
A |
|
|
x |
|
|
поверхности AD откоса |
|||
|
|
|
|
|
нагрузка отсутствует, то |
||||||
|
|
µ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
здесь следует |
принять |
|||
|
|
|
|
|
|
|
|
σ3 = 0, а направление σ1 |
|||
|
C |
|
|
|
|
|
|
будет |
совпадать |
с |
|
|
µ µ |
|
|
|
|
D |
|
направлением |
границы |
||
z |
σ1 |
B |
|
µ |
µ |
|
и составит с |
осью |
Oz |
||
α = 0 |
|
α = π/2−β |
β |
|
угол α = π/2 − β. Учиты- |
||||||
µ |
σ |
|
|||||||||
|
|
|
1 |
|
|
вая, что |
для невесомой |
||||
|
|
|
|
|
|
|
|
||||
|
Рис. 2.41. Схема к определению |
|
|
среды γ = 0, найденное |
|||||||
предельного давления на невесомый откос |
|
значение параметра α на |
|||||||||
|
|
|
|
|
|
|
|
границе не будет ме- |
|||
няться в пределах ABD. Тогда для этой области уравнения (2.6) |
|||||||||||
примут вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ = c ctgϕ , |
α = |
π |
− β. |
|
(2.55) |
|||
|
|
|
|
1− sin ϕ |
|
2 |
|
|
|
|
|
|
В области OAC минимального напряженного состояния имеем |
||||||||||
замкнутое решение (2.4) при γ = 0: |
|
|
|
|
|
|
|||||
|
|
|
σ = |
pu + c ctg ϕ , |
α = 0 . |
|
(2.56) |
||||
|
|
|
|
|
1+ sin ϕ |
|
|
|
|
|
|
В зоне радиального веера ABC параметры канонической системы уравнений α и σ связаны уравнением (2.12):
σ = σ0e−2tgϕ(α−α0 ) ,
где α0 и σ0 − значения параметров на границе AB. Подставляя сюда уравнения (2.55) и (2.56), имеем
pu + c ctgϕ |
= c ctgϕ e |
|
0− |
π |
|
||
|
2 |
. |
|||||
|
|
|
|
−2tgϕ |
|
+β |
|
1+ sin ϕ |
1− sin ϕ |
|
|
|
|
||
Окончательно выражение для предельного давления на невесомый откос примет вид:
|
1 |
+ sin ϕ |
|
(π−2β)tgϕ |
|
|
||
pu |
= |
|
|
|
e |
|
−1 c ctgϕ. |
(2.57) |
1 |
− sin ϕ |
|
||||||
|
|
|
|
|
|
|||
150

Размеры зон предельного равновесия нетрудно установить, используя уравнения логарифмических спиралей (2.11), которыми представлены характеристики 1-го семейства в зоне веера ABC. При этом следует помнить, что обозначения, принятые в формуле (2.11), введены на рис. 2.6.
2.3.3. Равноустойчивый контур откоса
Как уже говорилось, собственный вес является существенным фактором, влияющим на устойчивость склонов. Рассмотрим задачу о равноустойчивом очертании естественного откоса. Расчетная схема показана на рис. 2.42, а.
а) |
|
b |
pu |
= γh пр |
|
б) |
|
b |
pu |
> γh пр |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
O |
|
|
A |
|
x |
O |
|
|
A |
x |
σ1 |
|
I |
M |
|
σ1 |
|
I |
|
|
|
µ |
|
|
µ |
|
|
|
||||
α = 0 |
|
|
α = β M |
|
α = 0 |
|
II |
|
||
|
C |
|
III |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
|
|
|
B |
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
D |
|
|
|
|
D |
|
z |
|
|
|
|
|
z |
|
|
|
Рис. 2.42. Равноустойчивый контур склона:
а − при давлении на бровке, равном весу вертикального откоса предельной высоты; б − при большем давлении на бровке
Грунт может держать вертикальный откос, максимальная высота которого hпр рассчитывается по формуле (2.54). Очевидно, что если высота откоса будет меньше, то предельное состояние в нем не достигается. Следовательно, чтобы склон находился в предельном состоянии, необходимо на границе OA приложить давление pu, равное бытовому давлению от веса слоя грунта мощностью hпр:
151

p |
= γh |
= |
|
2ccosϕ |
. |
(2.58) |
|
|
|||||
u |
ï ð |
|
1− sin ϕ |
|
||
Теперь в откосе можно выделить две зоны − зона минимального напряженного состояния OAC и приоткосный участок ACD. В зоне OAC согласно (2.4) имеют место равенства:
σ = |
γz + pu |
+ c ctgϕ |
, α = 0 . |
(2.59) |
||
1 |
+ sin ϕ |
|||||
|
|
|
||||
Линии скольжения в OAC представлены прямыми:
x= ±z tg + C .
Вприоткосном участке ACD возникает необходимость численной реализации канонической системы уравнений ТПРГ. Обратим внимание, что, несмотря на перелом поверхности в точке A, эта точка не является особой, и в ней не происходит скачкооб-
разного изменения параметров σ и α. В самом деле, приближаясь к точке A слева, среднее приведенное напряжение исходя из (2.58) и (2.59) составит (z = 0):
|
|
2ccosϕ |
+ c ctgϕ |
|
|
|
|
|
|
σ = |
1− sin ϕ |
= |
ccosϕ + c ctg ϕ |
= |
|
sin ϕ +1 |
c ctg ϕ = |
||
|
|
||||||||
|
1+ sin ϕ |
1− sin2 ϕ |
1− sin2 ϕ |
||||||
|
|
|
|
|
|||||
= 1c−ctgsinϕϕ.
Справа от точки A, учитывая, что на свободной поверхности AD откоса σ3 = 0, из закона Кулона–Мора (1.15), имеем:
σ1 + 0 = (σ1 + 0 + 2ñ ctgϕ)sin ϕ,
2ccosϕ
σ1 = 1− sin ϕ ,
отсюда согласно (1.30) среднее приведенное напряжение запишется в виде:
σ = |
1 |
|
2ccosϕ |
+ 0 |
|
+ c ctgϕ = |
|||||
|
|
|
|
||||||||
2 |
1− sin ϕ |
||||||||||
|
|
|
|
|
|
(2.60) |
|||||
|
|
|
|
|
|
|
|
||||
= |
ccosϕ + c ctgϕ − ccosϕ |
= |
c ctgϕ |
. |
|||||||
|
|
||||||||||
|
|
|
|
1− sin ϕ |
|
|
1− sin ϕ |
||||
152
