
Лабораторная работа 8
.docГосударственное образовательное учреждение высшего профессионального образования
|
|
«Московский государственный технический университет имени Н.Э. Баумана» (МГТУ им. Н.Э.Баумана) |
Факультет: Фундаментальные науки
Кафедра: ФН4, «Физика»
Группа: ФН4-71
ЛАБОРАТОРНАЯ РАБОТА №8
по дисциплине
«Вычислительная физика»
Применение интерполяционных многочленов.
Преподаватель: доцент, к.ф.-м.н. Хасаншин Р. Х.
Студенты: Шиков Е.А. , Румянцев Д.Р.
Вариант: 5
Москва, 2014
Оглавление.
|
Теоретическая часть. |
3 |
|
Задание |
12 |
|
Код программы. |
13 |
|
Результаты вычислений. |
15 |
|
Вывод. |
22 |
|
|
|








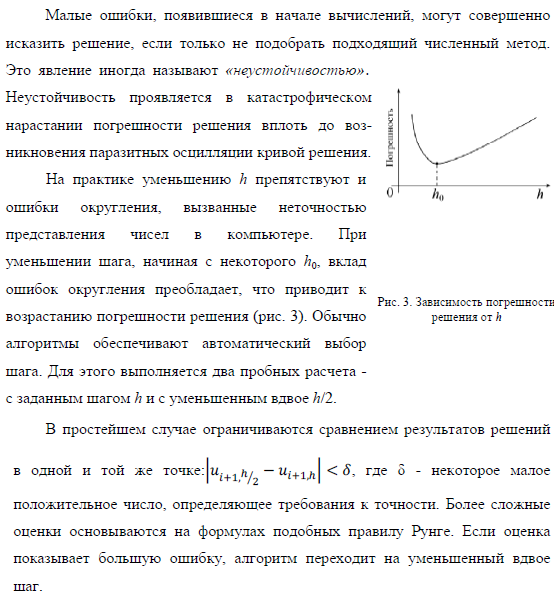
Задание.
Каждой «паре» решить свое дифференциальные уравнения, используя следующие методы:
Метод Эйлера
![]() ;
(1)
;
(1)
Модифицированный метод Эйлера
![]() ,
,
![]() ;
(2)
;
(2)
Усовершенствованный метод Эйлера
![]() ;
(3)
;
(3)
Метод Рунге-Кутта четвертого порядка
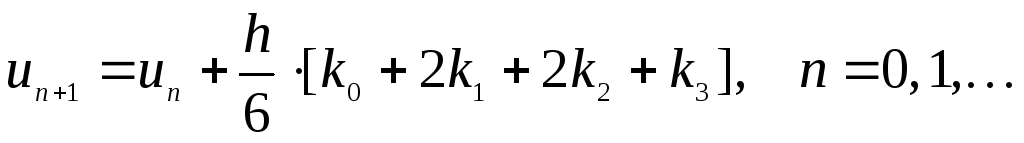 (4)
(4)
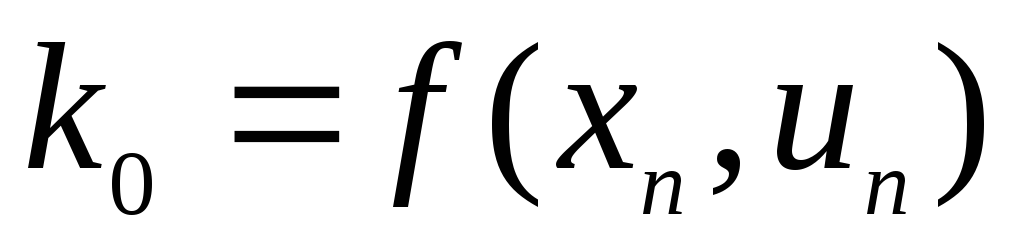 ,
,
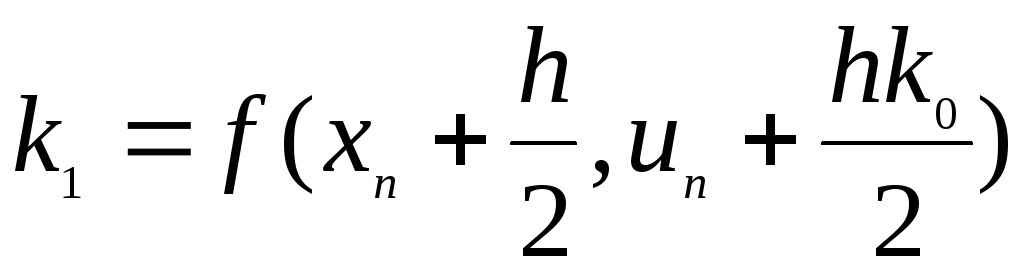 ,
,
![]() ,
,
![]() .
.
А).
![]() ,
,
![]() ,
,
![]() [0, 2]
[0, 2]
Б. Методом Эйлера и методом Эйлера-Кромера решить задачи Коши из Методического пособия (задачи о колебаниях)
Текст программы.
Задача А. /* double f1(double x, double u) //Задача для пары 5
{
return (2*x*pow(u,2))/(1-pow(x,2));
}
double f0(double x) //Решенное дифф урав для точного решения пара 5
{
return 1/(log(-pow(x,2)+1)+1);
}*/
double f1(double x, double u) //Задача для пары 3
{
return (4*x+2*u)/(2*x+1);
}
double f0(double x) //Решенное дифф урав для точного решения пара 3
{
return 2*(x+1)+(log(2*x+1))*(2*x+1);
}
/* double f1(double x, double u) //Задача для пары 8
{
return 1/(2*u+x);
}
double f0(double x) //Решенное дифф урав для точного решения пара 8
{
return -x/2-1;
}*/
double f2(double t) //Для задачи Б
{
double l=1, x0=1, w0=0.5, teta=sqrt(pow(l,2)-pow(w0,2));
return x0*exp(-l*t)*(cosh(teta*t)+l/teta*sinh(t*teta));
}
double b=2,a=0,u0=2; //Начальные условия задачи A
double l=1, x0=1, w0=0.5, a1=0, b1=6/l; //Начальные условия задачи Б
double h,N,P,k0,k1,k2,k3;
double x[300],y0[300],y1[300],y2[300],y3[300],y4[300],yp2[300], yp3[300], dy1[300],dy2[300],dy3[300],dy4[300];
double v1[300],v2[300],f[300],x1[300],x2[300],osh1[300],osh2[300], osh3[300], t[300];
ofstream myfile;
/// <summary>
/// Summary for Form1
/// </summary>
public ref class Form1 : public System::Windows::Forms::Form
{
public:
Form1(void)
{
InitializeComponent();
//
//TODO: Add the constructor code here
//
}
protected:
/// <summary>
/// Clean up any resources being used.
/// </summary>
~Form1()
{
if (components)
{
delete components;
}
}
Задача Б.
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
N=N.Parse(this->textBox1->Text);
x[0]=a; y1[0]=u0; y2[0]=u0; y3[0]=u0; y4[0]=u0; y0[0]=u0; dy1[0]=0; dy2[0]=0; dy3[0]=0; dy4[0]=0;
t[0]=0; f[0]=1, v1[0]=0, v2[0]=0,x1[0]=1,x2[0]=1,osh1[0]=0,osh2[0]=0;
if (checkBox1->Checked)
{
h=(b-a)/N;
for (int i=0;i<=N;i++)
{
x[i+1]=x[i]+h;
y1[i+1]=y1[i]+h*f1(x[i],y1[i]);
y2[i+1]=y2[i]+0.5*h*(f1(x[i],y2[i])+f1(x[i+1],y2[i]+h*f1(x[i],y2[i])));
y3[i+1]=y3[i]+h*f1(x[i]+0.5*h,y3[i]+0.5*h*f1(x[i],y3[i]));
k0=f1(x[i],y4[i]);
k1=f1(x[i]+h/2,y4[i]+h*k0/2);
k2=f1(x[i]+h/2,y4[i]+h*k1/2);
k3=f1(x[i]+h,y4[i]+h*k2);
y4[i+1]=y4[i]+h/6*(k0+2*k1+2*k2+k3);
y0[i+1]=f0(x[i+1]);
dy1[i+1]=abs(y0[i+1]-y1[i+1]);
dy2[i+1]=abs(y0[i+1]-y2[i+1]);
dy3[i+1]=abs(y0[i+1]-y3[i+1]);
dy4[i+1]=abs(y0[i+1]-y4[i+1]);
}
}
if (checkBox2->Checked)
{
h=(b1-a1)/N;
for (int i=0;i<=N;i++)
{
t[i+1]=h*(i+1);
f[i+1]=f2(t[i]);
v1[i+1]=v1[i]+h*(-2*l*v1[i]-pow(w0,2)*x1[i]);
x1[i+1]=x1[i]+h*v1[i];
v2[i+1]=v2[i]+h*(-2*l*v2[i]-pow(w0,2)*x2[i]);
x2[i+1]=x2[i]+h*v2[i+1];
osh1[i+1]=f[i+1]-x1[i+1];
osh2[i+1]=f[i+1]-x2[i+1];
}
}
}
Результаты.
Таблица решение задачи А.
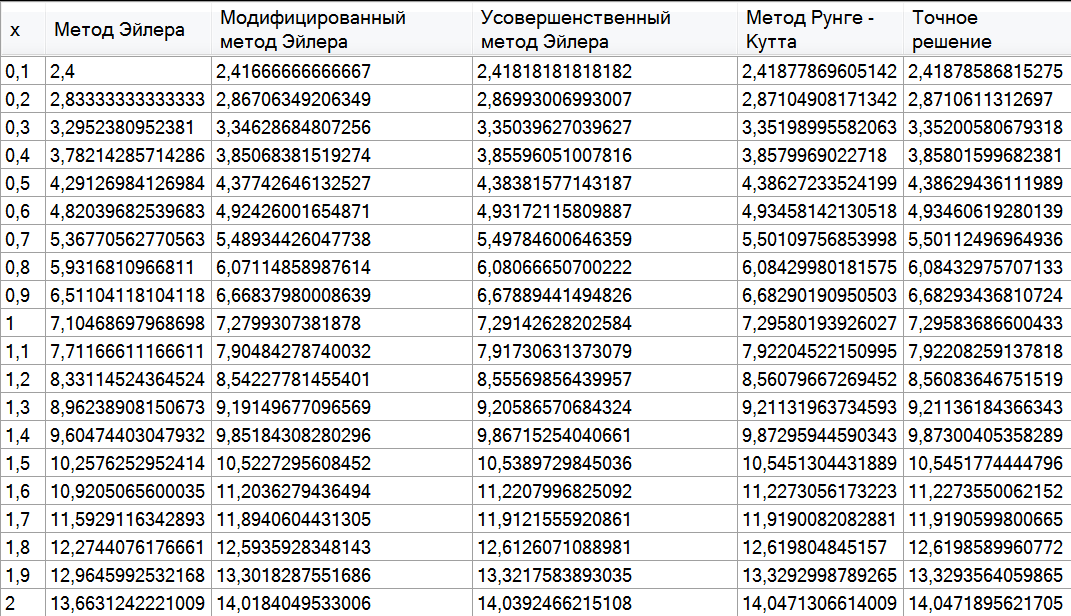
Погрешность задачи А.
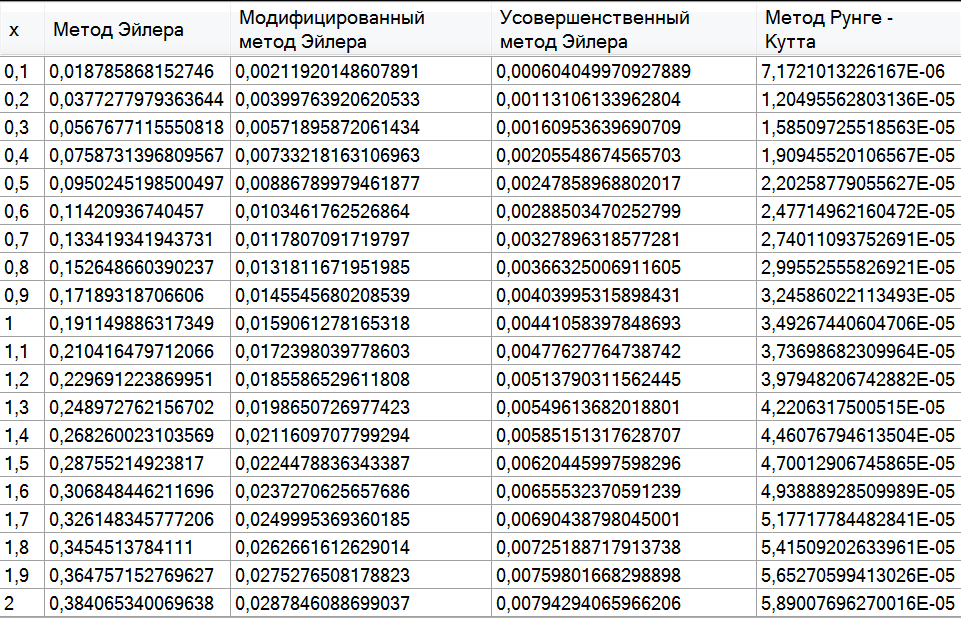
Таблица решение задачи Б
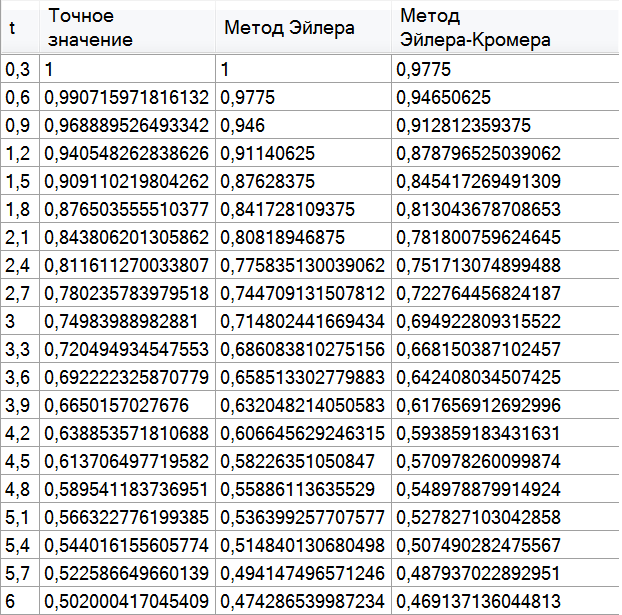
Таблица погрешность Б.
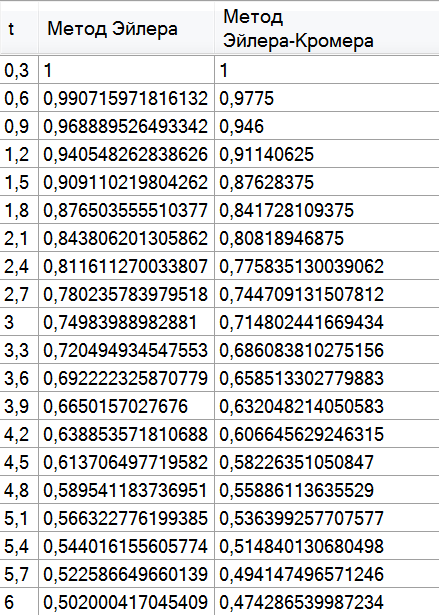
Задача
А.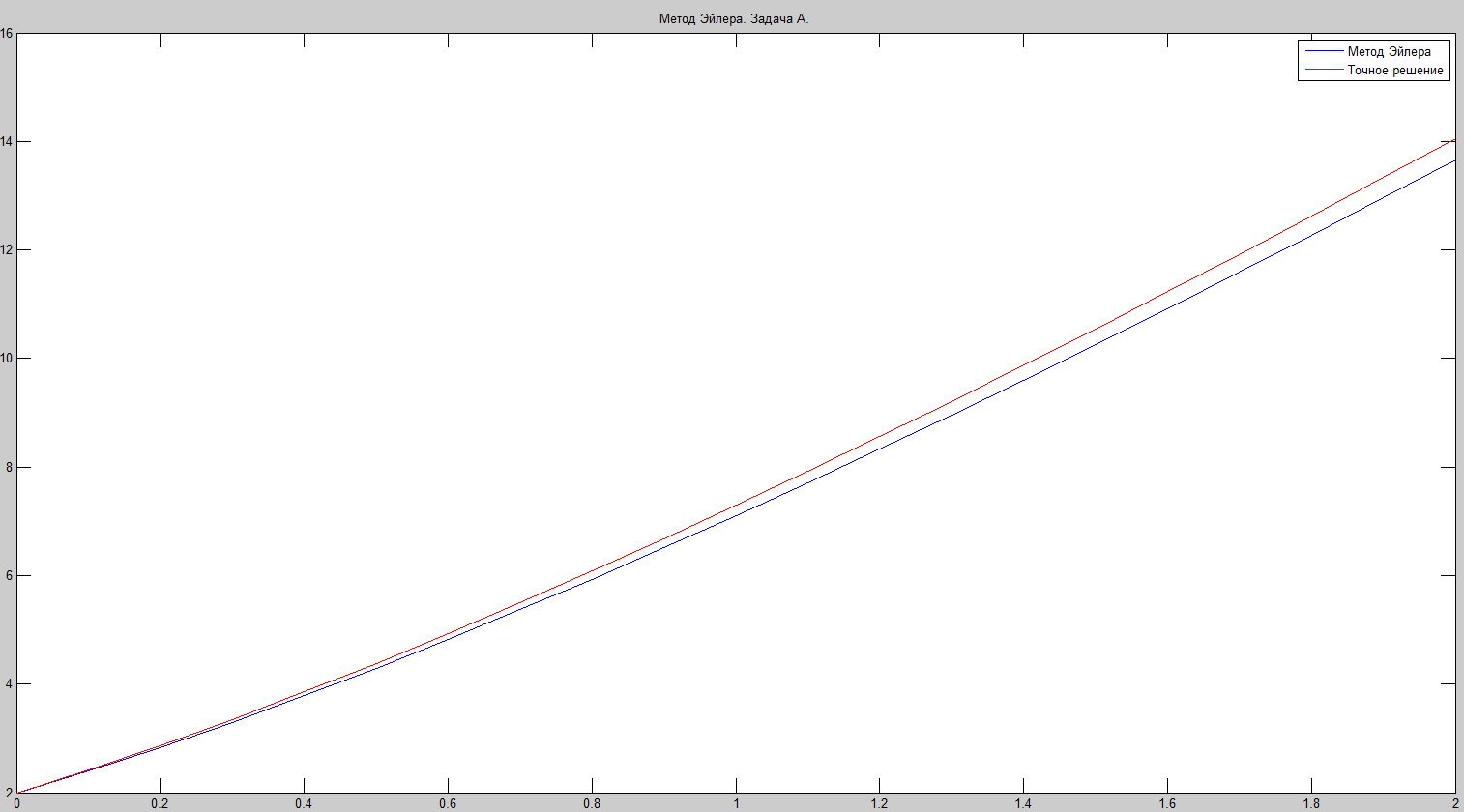
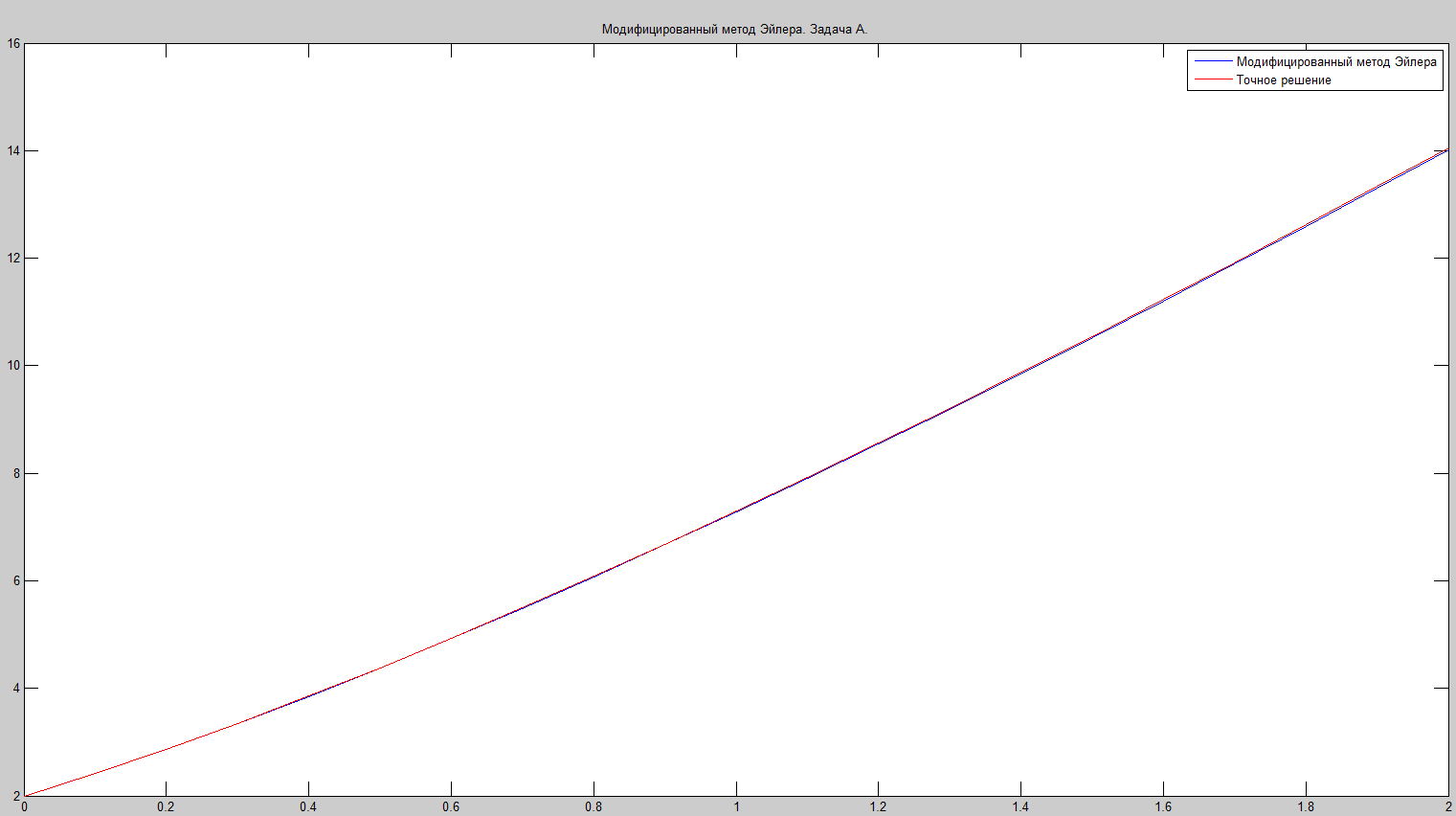
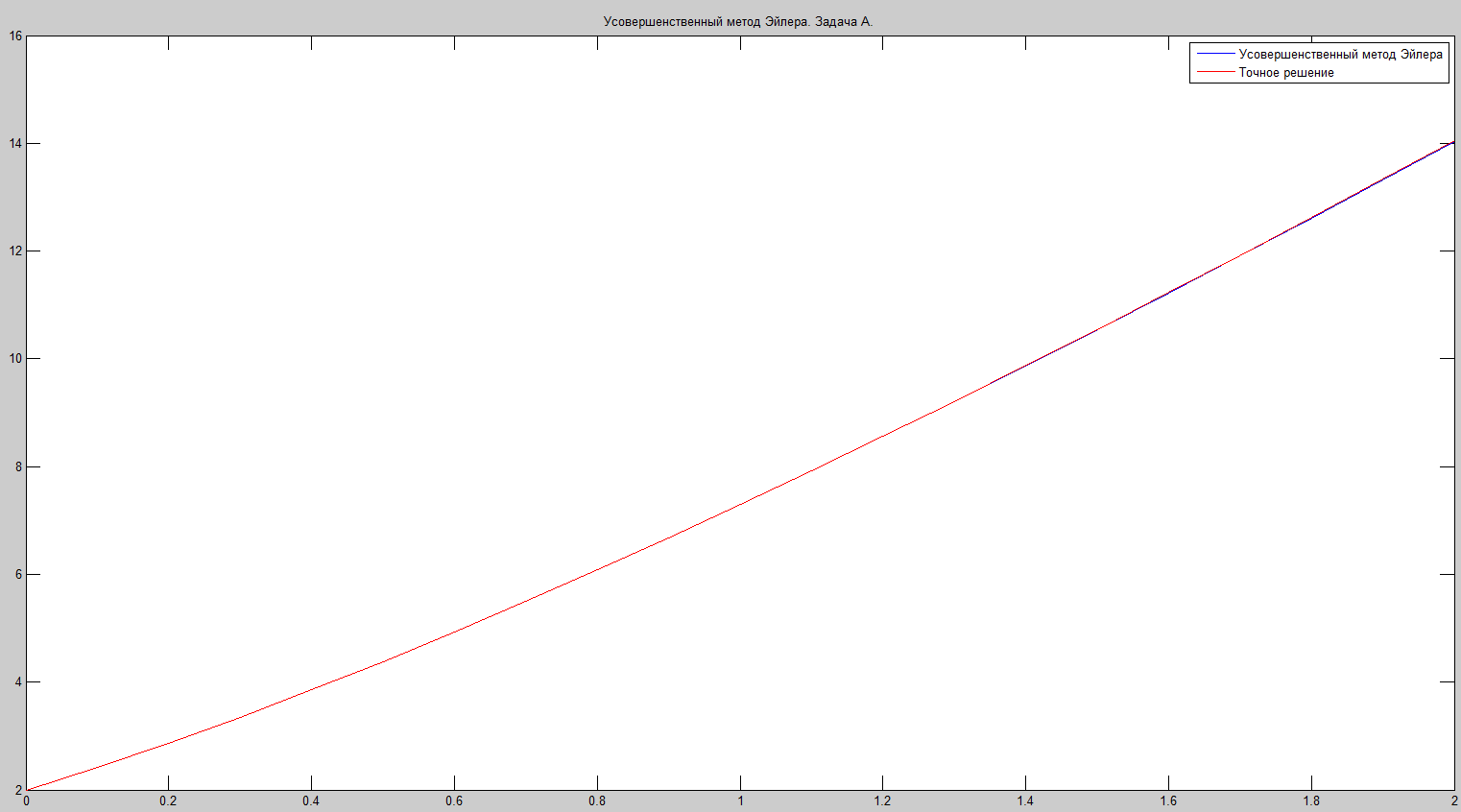
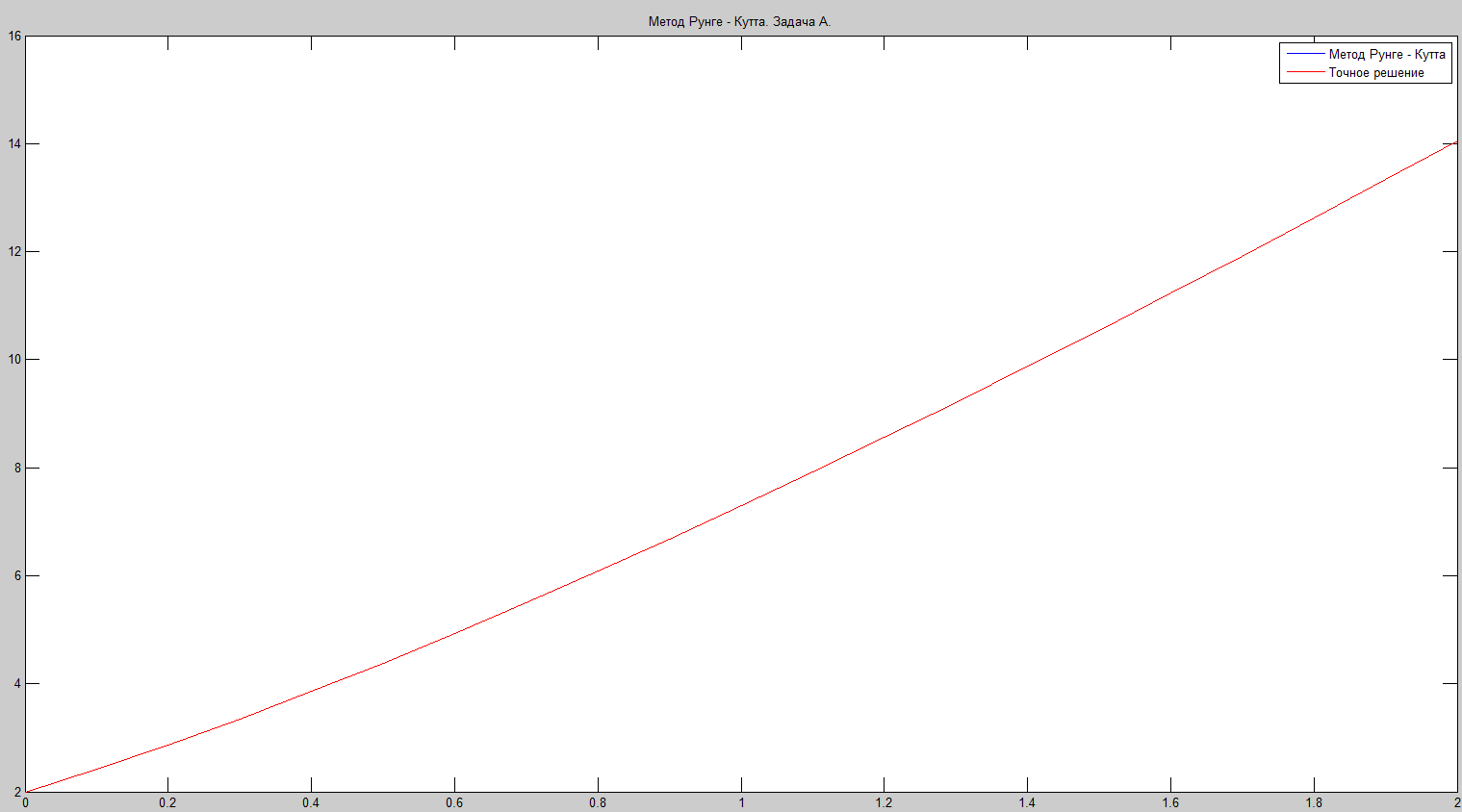

Метод Рунге-Кутта дает самое лучшее приближение к точному решению за счет высокого порядка точности. Но появляется необходимость производить по 4 вычисления функции для каждой точки, что связано с большим количеством вычислений.
Задача Б.
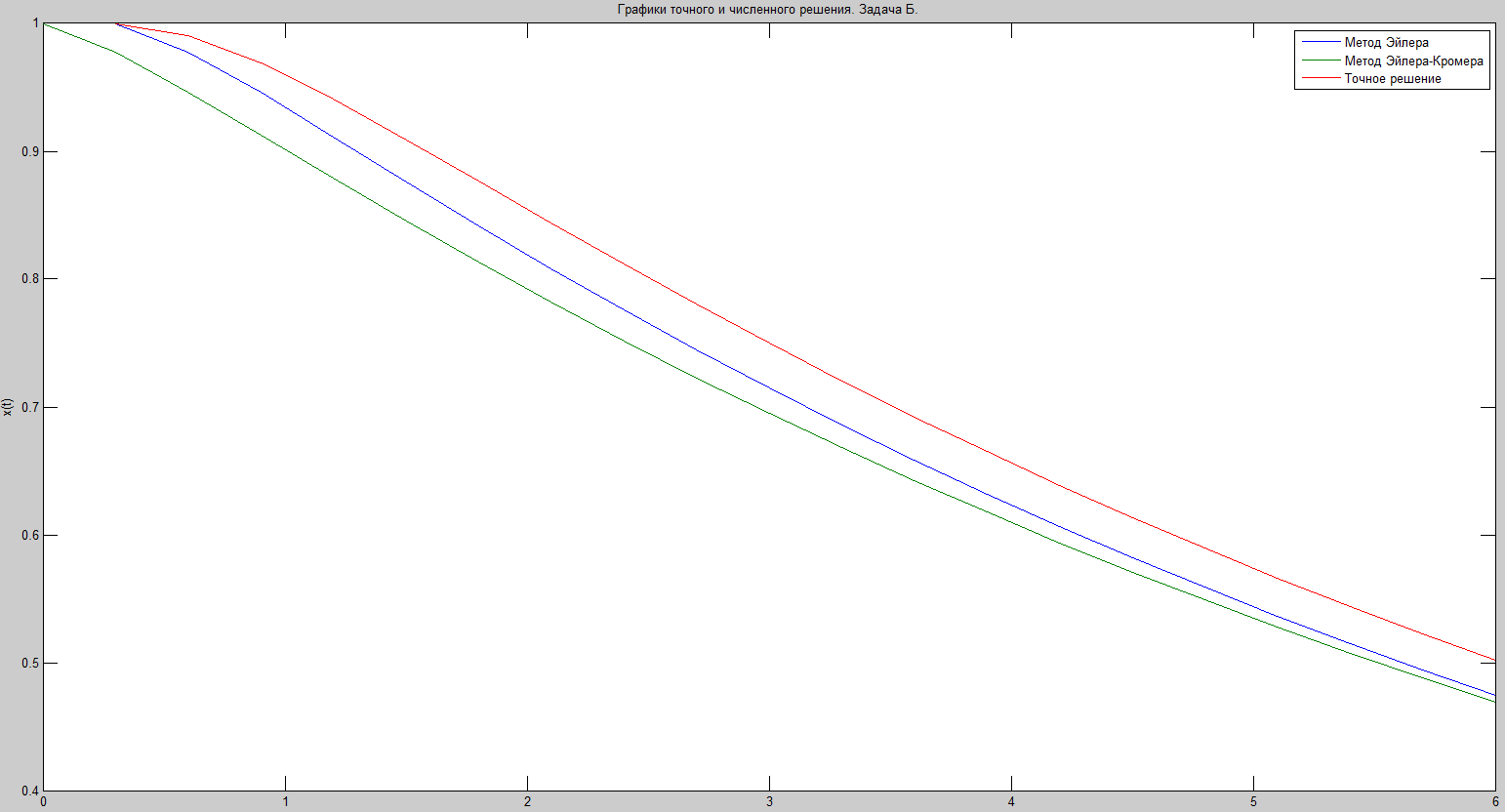
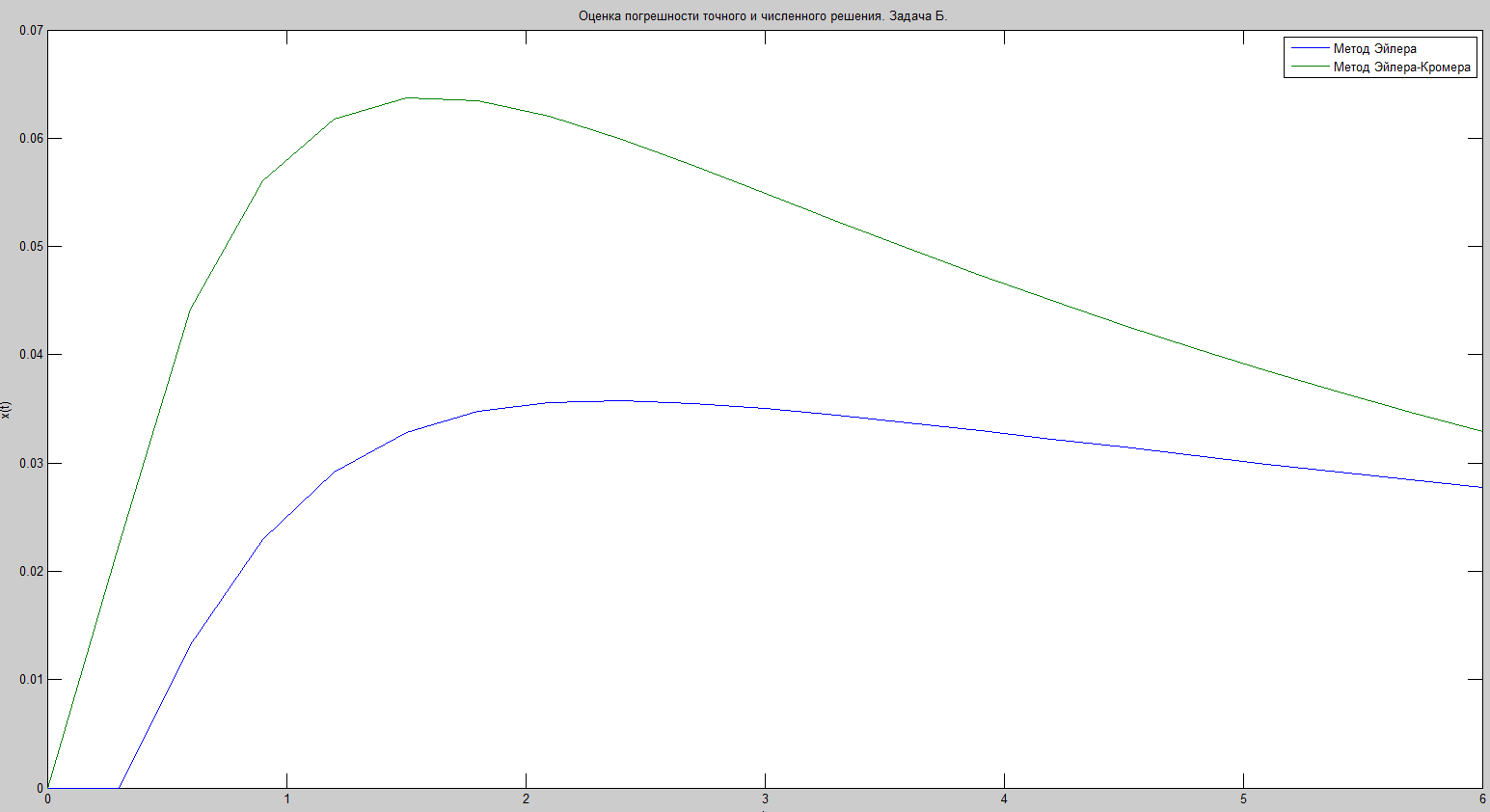
Вывод.
Метод Эйлера имеет глобальную погрешность первого порядка и не является достаточно точным методом численного решения ОДУ и имеет большую дисперсию по сравнению с точным решением при больших N. Метод Эйлера-Коши имеет глобальную погрешность 2 порядка точности, я является более точным методом решения , чем явный метод Эйлера, за счет поиска первого приближения к начальному приближению точного решения и его уточнения. Усовершенствованный метод Эйлера так же имеет 2 порядок точности. Все они имеет алгоритм решения предиктор-корректор. На стадии предиктор мы ищем первое приближение начального приближения, а на стадии корректор применяем его для поиска более точного начального приближения.
Метод Рунге-Кутта имеет 4 порядок точности и является лучшим численным методом решения ОДУ из перечисленных выше. Это преимущество достигается за счет четырехкратного вычисления правой части дифференциального уравнения на каждом шаге, вместо обычного дифференцирования правой части для поиска второй и последующей производной. Самым большим недостатком является необходимость проводить очень большое количество вычислений. Но он компенсируется высокой точностью метода и дает нам возможность использовать большой шаг.
Для решения уравнения колебаний используют метод Эйлера-Кромера, который, не смотря на 1 порядок точности, имеет меньшую погрешность, чем обычный метод Эйлера. то достигается за счет вычисления n+1 координаты используется значение n+1 скорости, а не предыдущей.
|
|
|

