
lektsia_2_kurs_ITF
.pdf
и по формуле Ньютона-Лейбница будем иметь
|
a |
a |
|
(13) |
||
P x |
|
|
|
|
. |
|
|
|
|
|
|
||
Пример 1. Пусть случайная |
величина |
X |
распределена |
по |
||
нормальному закону с параметрами a 30, 10. Найти вероятность того, что X примет значение, принадлежащее интервалу 10;50 .
Решение. По формуле (13) имеем:
P 10 |
|
50 30 |
|
|
10 30 |
|
2 2 2 2 |
x 50 |
10 |
|
|
10 |
|
||
|
|
|
|
|
|
2 0,4772 0,9544.
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X от ее математического ожидания по абсолютной величине меньше заданного положительного числат.е. найти P x a .
Эта вероятность находится по формуле
|
|
|
P |
|
x a |
|
|
|
|
|
|
|
|
|
|
|
(14) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример |
2. Пусть случайная |
|
|
|
|
|
|
||||||||||||||||
величина X |
распределена по |
||||||||||||||||||||||
нормальному закону с параметрами a 20, 10. Найти P |
|
x 20 |
|
|
3 . |
||||||||||||||||||
|
|
||||||||||||||||||||||
Решение. Используя формулу (14) |
имеем: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P |
x 20 |
|
3 2 |
|
|
|
2 0,3 2 0,1179 0,2358. |
|
|||||||||||||||
|
10 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ЗАКОН БОЛЬШИХ ЧИСЕЛ. НЕРАВЕНСТВО ЧЕБЫШЕВА |
|||||||||||||||||||||||
Теорема. |
Для |
любой |
|
|
случайной |
величины |
X при |
каждом |
|||||||||||||||
положительном числе имеет место неравенство |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
P |
|
X M x |
|
|
D x |
. |
|
|
|
|
|
(1) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Неравенство (1) называется неравенством Чебышева. |
|
|
|
|
|
|
|||||||||||||||||
91

Пример. Пусть случайная величина X имеет D X 0,001. Какова вероятностьтого, что X отличается от M X более чем на 0,1?
Решение. По неравенству Чебышева имеем:
P X M x 0,1 D 2x 00,001,01 0,1.
Примечание. Отметим другую форму неравенства Чебышева. Т.к. событие, выражаемое неравенством X M x , противоположно событию, выражаемому неравенством X M x , то
P X M x P X M x 1.
Отсюда с учетом неравенства (1) получаем такую форму неравенства Чебышева
(2)
Теорема Чебышева. Если дисперсии независимых случайных величин
|
X1,X2,...,Xn |
ограничены одной и той же постоянной C, D xi C i |
|
, |
|||||||||||||||||||||||||
1,n |
|||||||||||||||||||||||||||||
то, каково |
бы |
ни |
было |
0, вероятность |
выполнения |
неравенства |
|||||||||||||||||||||||
|
|
M |
|
|
|
, |
где |
|
1 X1 .... Xn , будет |
сколь угодно близка к |
|||||||||||||||||||
|
X |
X |
|
X |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
единице, если число случайных величин n достаточно велико, т.е. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
lim P |
|
|
|
M |
|
|
|
1. |
|
(3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
X |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частный случай Т. |
Чебышева. Если все Xk имеют |
одинаковые |
|||||||||||||||||||||||||
математические |
ожидания |
|
|
|
M X1 M X2 ... M Xn a, |
D Xk c, |
|||||||||||||||||||||||
k 1,2,....,n , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
lim P |
|
|
|
a |
|
1. |
|
(4) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
92
ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ ПОНЯТИЕ СКАЛЯРНОГО ПОЛЯ
Если каждой точке M из ставится в соответствие по известному закону некоторое число u u M , то говорят, что в области задано скалярное поле u .
Иными словами, задать скалярное поле - это означает задать скалярную функцию u u M , называемую функцией поля. Запись u M означает, что величина u является, как говорят, функцией точки. Заметим, что областьюможет быть и все пространство.
Если величина u u M не зависит от времени t , то скалярное поле u называется стационарным или установившимся.
Поле температуры внутри нагретого тела, поле плотности массы, поле распределения потенциала в электрическом поле - примеры скалярных полей.
Запись u u M не предполагает введения в пространстве никакой системы координат. Если же пространство отнесено к некоторой системе координат, например к прямоугольной системе координат Oxyz , то задание точки M равносильно заданию ее координат x,y,z в этой системе и функция поля u M превращается в обычную функцию трех переменных u x,y,z . Мы всегда будем предполагать, что эта функция имеет непрерывные частные производные.
Можно ввести в пространстве и другие системы координат, например цилиндрическую и сферическую. В цилиндрической системе координат функция поля u u r, ,z , в сферической u u r, , .
ПОВЕРХНОСТИ УРОВНЯ
Скалярные поле часто изображаются геометрически с помощью так называемых поверхностей уровня.
93

Поверхностью уровня скалярного поля u M называется множество точек пространства, в которых функция поля имеет постоянное значение.
Уравнение поверхности уровня в прямоугольной системе координат Oxyz имеет вид u x,y,z c, где c - некоторая постоянная.
Указанный способ изображения скалярного поля удобен, если речь идет о плоском скалярном поле, т.е. о поле, заданном в плоской области.
Функция u этого поля зависти только от двух переменных x и y . Поэтому плоские скалярные поля геометрически изображают с помощью линий уровня.
В случае поля температур на плоскости линии уровня называются изотермами, в случае поля давления - изобарами и т.д.
ЛАПЛАСИАН СКАЛЯРНОГО ПОЛЯ
Дифференциальный оператор второго порядка, введенный для скалярного поля u u x,y,z
u x2u2 y2u2 z2u2
называется оператором Лапласа или лапласианом.
Выражение оператора Лапласа в цилиндрических координатах имеет
вид:
u r2u2 1r ur r12 2u2 z2u2 .
Последнее выражение часто бывает удобно записывать в таком виде:
u |
1 |
u |
|
1 2u |
|
2u |
|
||||
|
|
r |
|
|
|
|
|
. |
|||
r |
|
r2 2 |
z2 |
||||||||
|
r |
r |
|
|
|
||||||
В случае сферических координат выражение оператора Лапласа имеет вид:
u |
2u |
|
2 u |
|
cos |
|
u |
|
1 |
|
2u |
|
1 |
|
|
2u |
. |
|
r2 |
r |
r |
r2 sin |
r2 |
|
2 |
r2 sin2 |
2 |
||||||||||
|
|
|
|
|
|
|
||||||||||||
Эту формулу еще записывают в виде:
94

|
|
|
|
1 |
2 u |
1 |
u |
1 |
|
2u |
|
|||||||
u |
|
|
|
|
r |
|
|
|
|
sin |
|
|
|
|
|
. |
||
|
|
|
|
|
|
r2 sin2 2 |
||||||||||||
|
|
|
r2 r |
r |
r2 sin |
|
|
|||||||||||
|
ПРОИЗВОДНАЯ ПОЛЯ ПО НАПРАВЛЕНИЮ |
|
||||||||||||||||
Определение. Производной скалярного поля |
u M |
|
в точке M по |
|||||||||||||||
направлению |
|
|
|
|
называется |
предел (если он существует) отношения |
||||||||||||
|
n |
|
|
|||||||||||||||
приращения |
u |
|
функции u M при смещении точки M в направлении |
|||||||||||||||
вектора n к величине этого смещения d MM1, когда последнее стремится к нулю и она обозначается символом un ,
т.е.
u |
lim |
u |
limu M1 u M . |
|
n |
d 0 |
d |
d 0 |
d |
Используют более удобную формулу для вычисления производной поля по направлению:
u |
u cos |
u cos u cos . |
(1) |
||||||||||||||||
n |
x |
y |
|
|
|
|
z |
|
|
|
|
||||||||
Пусть теперь дано скалярное поле |
u u M u x,y,z . |
|
|||||||||||||||||
Определение. Вектор |
u |
|
|
u |
|
|
|
|
|
u |
|
|
|
называется |
градиентом |
||||
i |
j |
k |
|||||||||||||||||
|
|
x |
y |
|
|
|
|
|
z |
|
|
|
|
||||||
скалярного поля u u M в точке M и обозначается |
|
||||||||||||||||||
|
|
gradu |
u |
|
|
u |
|
|
u |
|
. |
(2) |
|||||||
|
|
i |
j |
k |
|||||||||||||||
|
|
|
|
|
x |
y |
z |
|
|||||||||||
В плоском скалярном поле u u M u x,y градиент определяется равенством
gradu ux i uy j.
95

ВЕКТОРНОЕ ПОЛЕ. ВЕКТОРНЫЕ ЛИНИИ
Пусть - область в пространстве. Если каждой точке M из сопоставлен вполне определенный вектор a M , то говорят, что в области задано векторное поле a.
Заместим, что областью может быть и все пространство. Примерами векторных полей являются: поле силы тяжести, поле
скорости частиц текущей жидкости, поле электрической и магнитной
индукции, поле плотности электрического тока и т.д. В |
прямоугольной |
||||||||||||||||||||||
системе координат Oxyz вектор |
|
M записывается в виде |
|
|
|
||||||||||||||||||
a |
|
|
|
||||||||||||||||||||
|
|
M ax x,y,z |
|
ay x,y,z |
|
az x,y,z |
|
, |
|
|
|
||||||||||||
a |
i |
j |
k |
|
|
|
|||||||||||||||||
где ax, ay, az - проекции вектора заданного в точке M x,y,z |
соответственно |
||||||||||||||||||||||
на оси координат Ox, Oy, Oz . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Векторное поле |
называется однородным, если |
|
M |
- постоянный |
|||||||||||||||||||
a |
|||||||||||||||||||||||
вектор, т.е. ax, ay, az |
- постоянные величины. Примером однородного поля |
||||||||||||||||||||||
может служить, например, поле силы тяжести. |
|
|
|
||||||||||||||||||||
Векторное поле называется плоским, |
если проекции вектора |
|
M не |
||||||||||||||||||||
a |
|||||||||||||||||||||||
зависят от одной из трех переменных x,y,z |
и одна из проекций равна нулю, |
||||||||||||||||||||||
например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
M ax x,y |
|
ay x,y |
|
. |
|
|
|
|||||||||||
|
|
|
a |
i |
j |
|
|
|
|||||||||||||||
С плоскими полями приходится встречаться в гидродинамике при изучении плоских течений жидкости, т.е. таких течений, когда все частицы жидкости движутся параллельно некоторой плоскости, причем скорости частиц, расположенных на одной и той же прямой, перпендикулярной к этой плоскости, одинаковы.
Векторной линией векторного поля называется линия, в каждой точке которой касательная совпадает с вектором, соответствующей этой точке.
Векторные линии в конкретных полях имеют ясный физический смысл. Так, если мы рассматриваем поле скоростей текущей жидкости, то векторные
96

линии суть линии тока этой жидкости, т.е. линии по которым движутся частицы жидкости.
В электростатическом поле векторные линии – это силовые линии этого поля. Например, в поле точечного заряда такими линиями будут лучи, ходящие из заряда. Для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
ПОТОК ВЕКТОРНОГО ПОЛЯ
Потоком вектора a M или потоком векторного поля a M через поверхность называется поверхностный интеграл
а M n0ds,
где n0 - единичный вектор нормали к поверхности в ее текущей точке M . Последнюю формулу еще записывают в виде
axdydz aydzdx azdxdy.
Т.о., вычисление потока вектора сводится к вычислению интегралов по поверхности.
ФОРМУЛАОСТРОГРАДСКОГО-ГАУССА. ДИВЕРГЕНЦИЯ
Формула Остроградского-Гаусса связывает поверхностный интеграл по замкнутой поверхности и тройной интеграл по пространственной области, ограниченной этой поверхностью. Эта формула является аналогом формулы Римана-Грина, связывающей криволинейный интеграл по замкнутой кривой с двойным интегралом по плоской области, ограниченной этой кривой.
Формула
|
P |
|
Q |
|
R |
|
|
|
|
|
|
|
|
|
Pdydz Qdzdx Rdxdy |
(1) |
|
|
x |
y |
dxdydz |
|
||||
|
|
|
z |
|
|
|
называется формулой Остроградского-Гаусса, где поверхностный интеграл берется по внешней стороне поверхности .
97

Если в формуле (1) функции P, Q, R рассматривать как проекции некоторого
вектора a M , то правая часть равна потоку вектора a M через замкнутую поверхность , а выражение
P Q R ,x y z
называется дивергенцией векторного поля a M и обозначается
diva M P Q R .
x y z
С учетом этого, формула Остроградского-Гаусса может быть переписана и в виде
|
|
|
|
an M ds diva |
M dv, |
(2) |
|
т.е. поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции этого поля, взятому по области, ограниченной этой поверхностью.
ЦИРКУЛЯЦИЯ И РОТОР ВЕКТОРНОГО ПОЛЯ
Под циркуляцией векторного поля a M по контуру L понимается следующий криволинейный интеграл по замкнутому пути L, снабженному направлением обхода:
ЦL 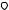 a dl,
a dl,
L
где a - проекция вектора поля a M на касательную к пути L в точке M , причем на этой касательной положительным считается то направление, которое совпадает с направлением обхода контура.
Ротором (вихрем) векторного поля |
|
|
|
|
|
|
|
|
M ax |
|
ay |
|
az |
|
|||||||||||||||
|
|
|
a |
a |
i |
j |
k |
||||||||||||||||||||||
называется вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
az |
|
a |
y |
|
|
|
ax |
|
az |
|
|
|
a |
y |
|
|
|
ax |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
y |
z |
i |
z |
x |
j |
x |
|
y |
|
k. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
98

Его обозначают через rota .
Таким образом rota ayz azy i azx axz j axy ayx k
или для удобства запоминания
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
k |
|||||||||||
|
|
|
|
|
|
|
|
|
. |
|||||||
rota |
||||||||||||||||
x |
|
y |
z |
|||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
ax |
|
ay |
|
az |
|
||||||||
ФОРМУЛА СТОКСА
Формула
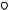 Pdx Qdy Rdz
Pdx Qdy Rdz
L
|
|
Q P |
|
R Q |
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
cos |
y |
cos |
|||||
|
|
|
y |
|
|
z |
|
||
называется формулой Стокса, где
P P x,y,z , Q Q x,y,z , R R x,
Интеграл в левой части формулы (1) равен
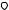 a dl ,
a dl ,
L
P |
|
R |
|
|
|
|
(1) |
||
z |
cos ds. |
|||
|
x |
|
|
|
y,z .
циркуляции вектора |
|
|
|
|
|
|
вдоль контура |
L. Интеграл в правой |
||||
a |
Pi |
Q j Rk |
||||||||||
|
|
|
|
|
через поверхность , |
|||||||
части представляет собой поток вектора rota |
|
|||||||||||
ограниченную контуром L. |
|
|
|
|
|
|
||||||
Следовательно, формулу Стокса в векторной форме можно записать |
||||||||||||
так: |
|
|
|
|
|
|
||||||
|
|
|
a dl rotn |
|
|
(2) |
||||||
|
|
|
ads, |
|||||||||
|
|
|
L |
|
|
|||||||
где
rotn a npnrota .
99
Формулу Стокса с помощью формулы связи поверхностных интегралов можно переписать в виде
|
|
|
|
|
Q P |
|
R Q |
P R |
|
||||||
Pdx Qdy Rdz |
|
|
|
|
|
|
|
|
|
|
dzdx. |
(3) |
|||
|
|
|
x |
dxdy |
y |
dydz |
|||||||||
L |
|
|
|
|
y |
|
|
z |
z |
|
x |
|
|||
|
В |
частности, |
если |
поверхность |
- |
область |
плоскости |
xOy, |
|||||||
ограниченная контуром L, то интегралы по dzdx и dydz обращаются в нуль и формула Стокса переходит в формулу Римана-Грина.
100
