Решение типовых примеров

Пример 1.1. Требуется найти неопределенный интеграл методом разложения

.

Решение. Используя правила интегрирования (см. приложение 8) исходный интеграл можно разложить в сумму интегралов

.

После преобразований подынтегральных функций получим сумму табличных интегралов

.

Пример 1.2. Требуется найти неопределенный интеграл методом замены переменной

.

Решение. Применим замену переменной вида , вычислим dt и выполним подстановку

.

В результате замены переменной получаем интеграл от показательной функции, который легко находится по таблице (см. приложение 9). После нахождения первообразной производим обратную замену переменной

.

Пример 1.3. Требуется найти неопределенный интеграл методом интегрирования по частям

.

Решение. В соответствии с формулой 9 приложения 8 положим , . Дифференцируя f и интегрируя dg имеем

.

Для нахождения последнего интеграла воспользуемся методом замены переменной. Пусть . В таком случае искомый интеграл может быть записан в виде

.

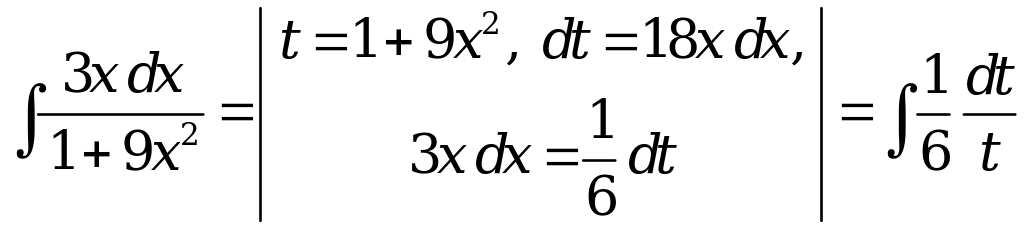В результате замены переменной получаем табличный интеграл (см. приложение 9, формула 2)

.

Таким образом, искомый интеграл может быть вычислен как

.

Тема 2. Определенный интеграл

Перед решением задач с использованием определенного интеграла следует разобраться в этом понятии и в понятии интегральной суммы. При решении задач следует опираться на геометрический смысл интегральной суммы и ее связь с определенным интегралом. Заметим, что определенные интегралы сохраняют все основные свойства неопределенных интегралов (см. приложение 8). Методы интегрирования в общих чертах также сохраняются, но существуют и некоторые изменения, связанные с появлением пределов интегрирования. Так, например, формула интегрирования по частям для определенного интеграла принимает вид

.

Следует обратить внимание, что формула вычисления площади фигуры, ограниченной сверху и снизу кривыми , , , а с боков прямыми ,

остается верной при любых знаках значений функций , .

Вопросы для самопроверки

1. В чем состоит отличие в реализации метода замены переменной под знаком и ?

2. Запишите интегральную сумму для функции на отрезке .

3. Что называется определенным интегралом функции на отрезке ?

4. Каков геометрический смысл определенного интеграла?

5. Перечислите основные свойства определенного интеграла.

7. Напишите формулу Ньютона-Лейбница.

8. Напишите формулу интегрирования по частям в определенном интеграле.

9. Как вычислить объем тела, образованного вращением плоской фигуры вокруг оси Ox? вокруг оси Oy?

Задание 2. вычислить указанные определенные интегралы.

Вариант 2.1	Вариант 2.2	Вариант 2.3
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.4	Вариант 2.5	Вариант 2.6
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.7	Вариант 2.8	Вариант 2.9
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.10	Вариант 2.11	Вариант 2.12
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.13	Вариант 2.14	Вариант 2.15
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.16	Вариант 2.17	Вариант 2.18
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.19	Вариант 2.20	Вариант 2.21
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.22	Вариант 2.23	Вариант 2.24
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.25	Вариант 2.26	Вариант 2.27
1. ;	1. ;	1. ;
2. .	2. .	2. .

Вариант 2.28	Вариант 2.29	Вариант 2.30
1. ;	1. ;	1. ;
2. .	2. .	2. .

Задание 3. Вычислить площадь фигуры, ограниченной линиями. Все линии и характерные точки построить в системе координат xOy.

3.1.	3.2.
3.3.	3.4.
3.5.	3.6.
3.7.	3.8.
3.9.	3.10.
3.11.	3.12.
3.13.	3.14.
3.15.	3.16.
3.17.	3.18.
3.19.	3.20.
3.21.	3.22.
3.23.	3.24.
3.25.	3.26.
3.27.	3.28.
3.29.	3.30.