
m32444_6
.docТЕМА 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В ЗАДАЧАХ 121-130 вычислить площадь, ограниченную графиками заданных функций (параболами).
-
121.
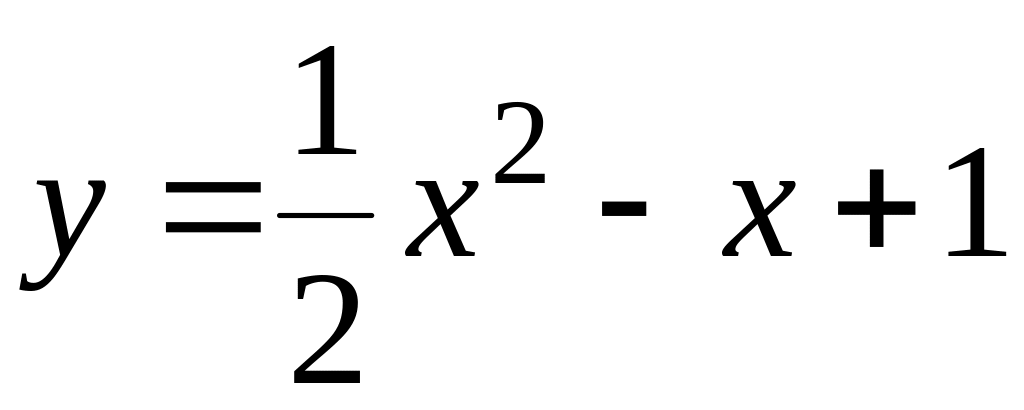 ;
;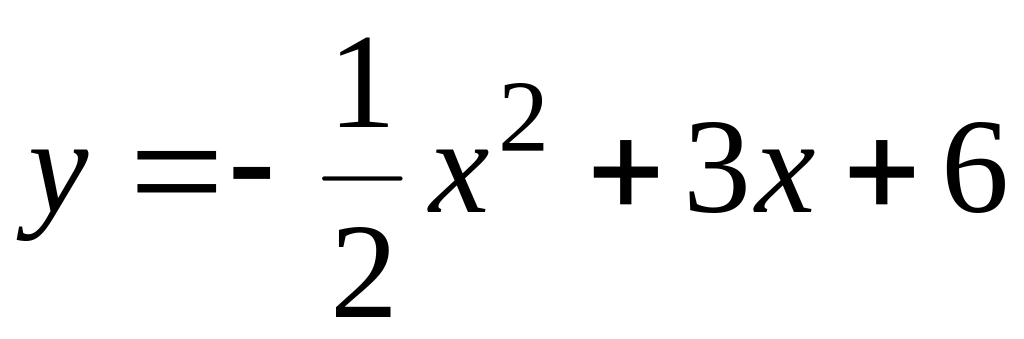 .
.122.
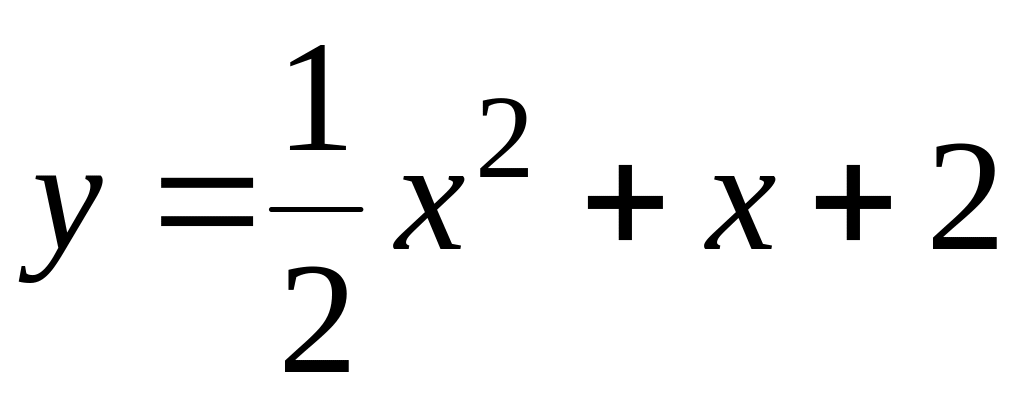 ;
;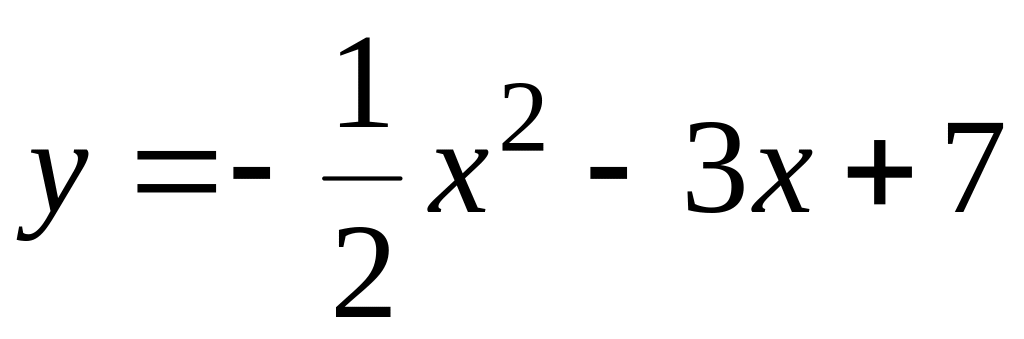 .
.123.
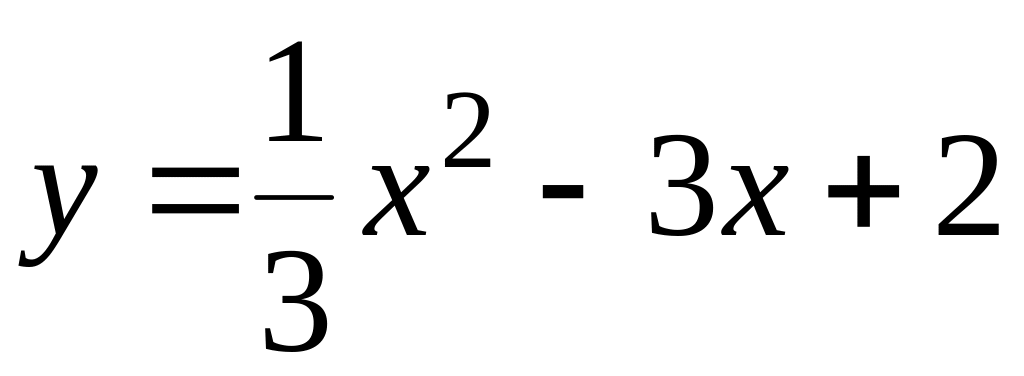 ;
; .
.124.
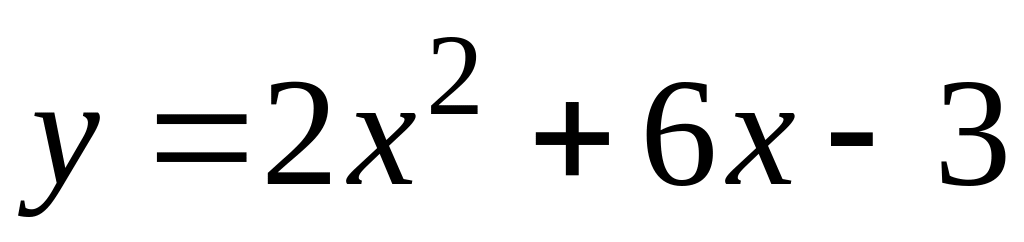 ;
;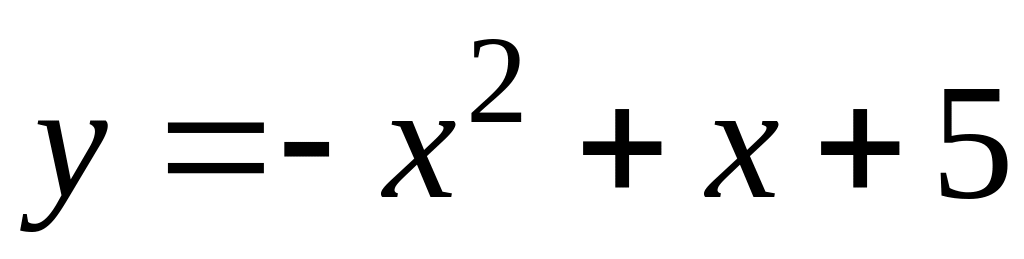 .
.125.
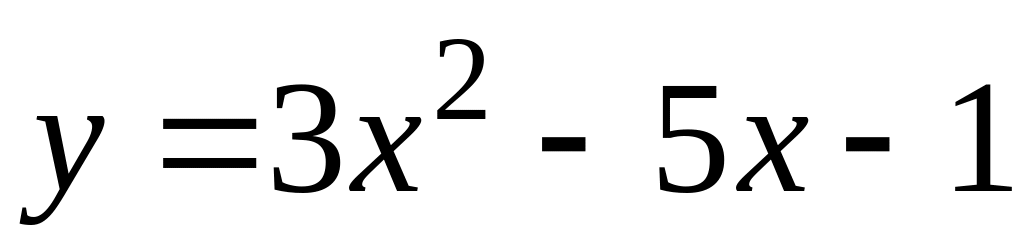 ;
;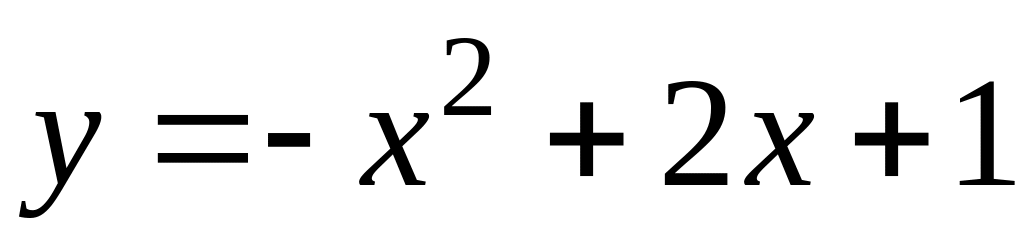 .
.126.
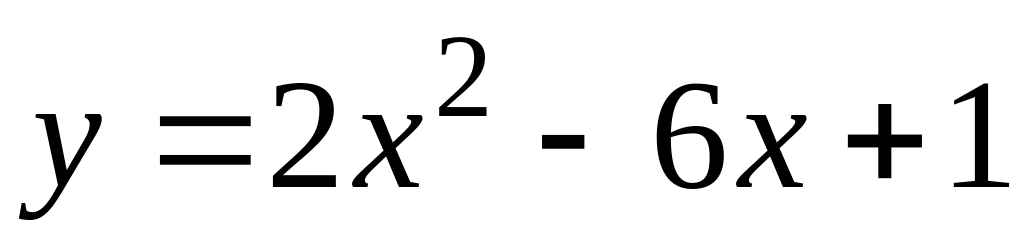 ;
;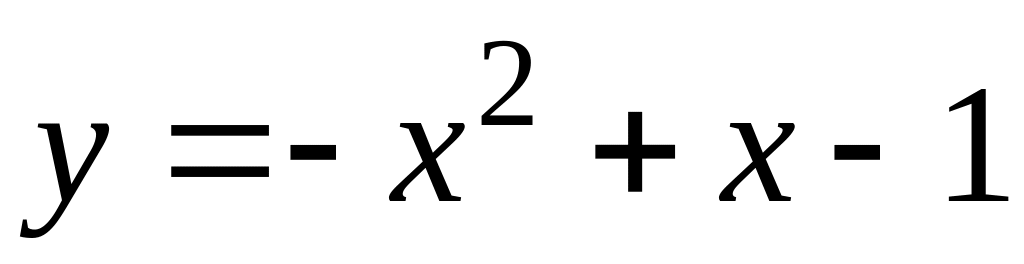 .
.127.
 ;
;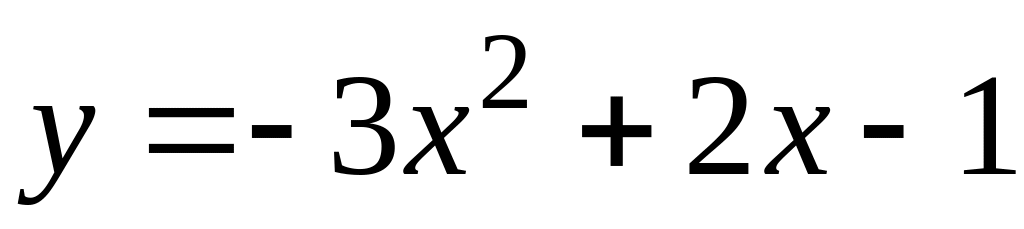 .
.128.
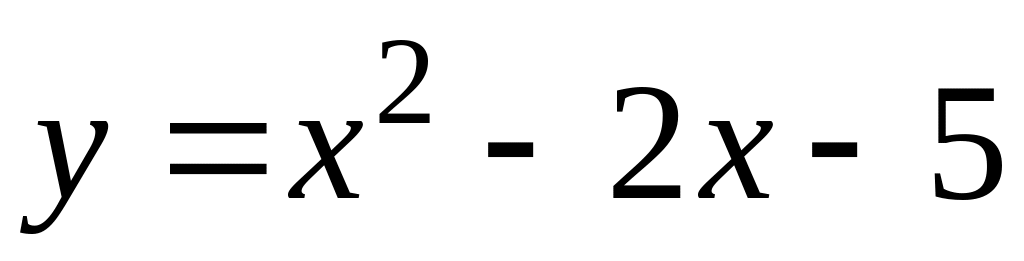 ;
;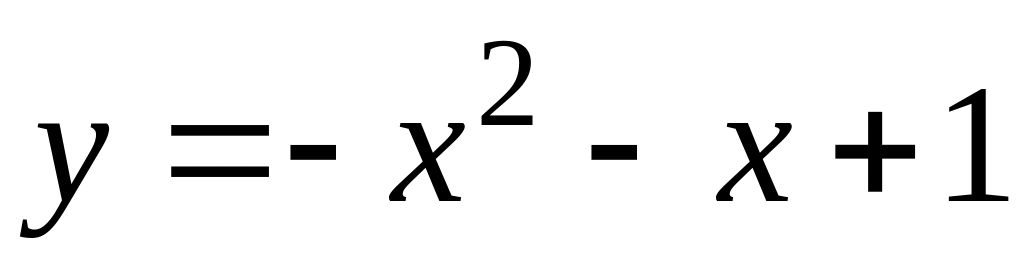
129.
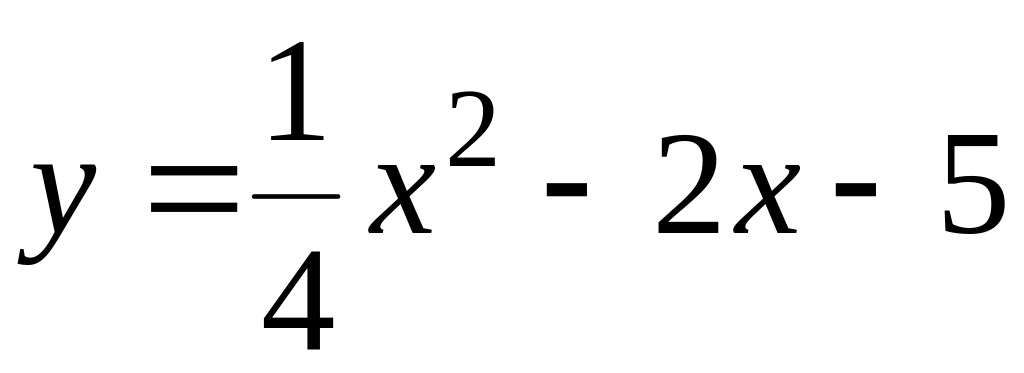 ;
;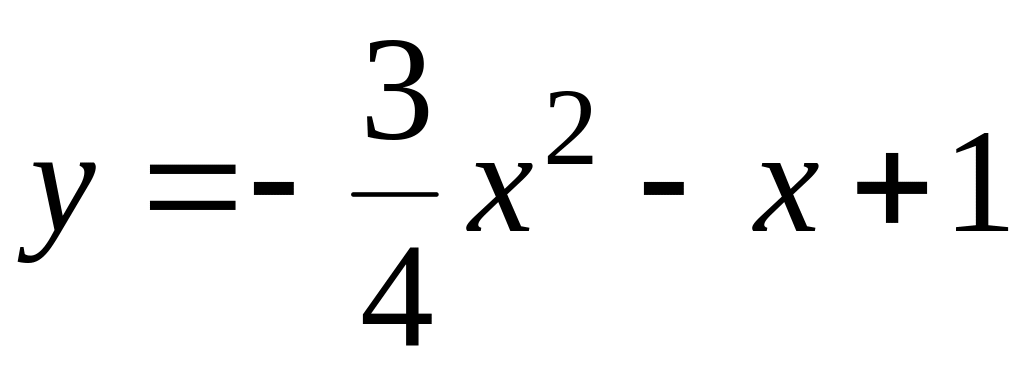 .
.130.
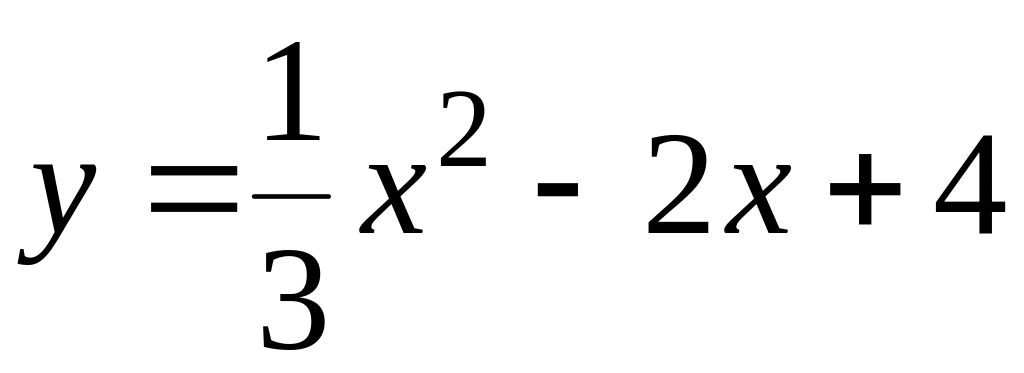 ;
; .
.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА.
Вычислить
площадь, ограниченную параболами
![]() и
(рис. 4).
и
(рис. 4).
Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
![]() =
=![]() .
.
Отсюда
![]() и
и
![]() ,
,
![]() .
.
Площадь
фигуры вычислим по формуле
![]() ,
где
,
где
![]() ,
,
![]()
кривые, ограничивающие фигуру (
кривые, ограничивающие фигуру (![]()
![]() ).
).
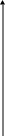

 y
y

- 1/3 1


 x
x

Рис. 4
В нашем случае площадь равна
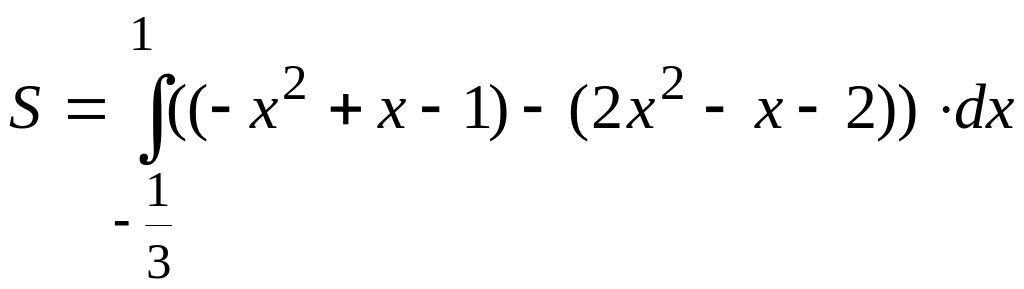 =
=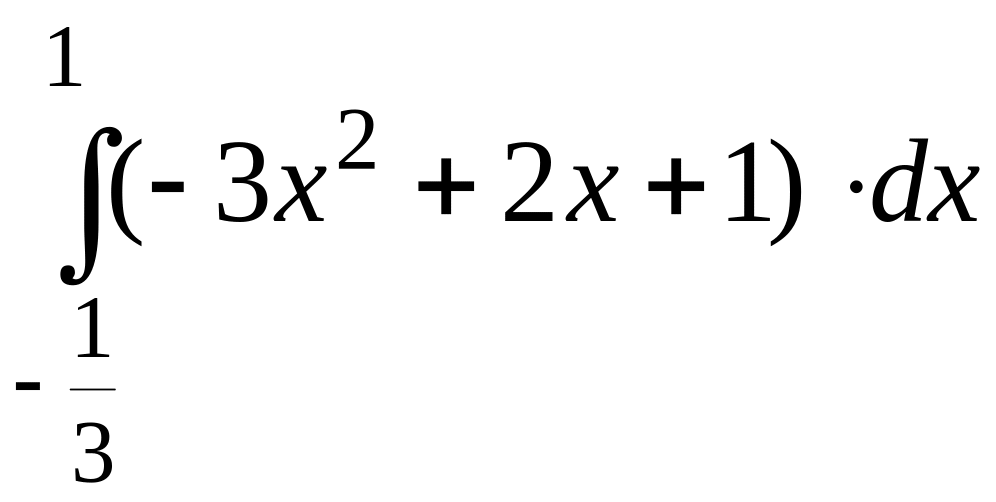 =
=
=![]() .
.
В
ЗАДАЧАХ 131-140
 требуется
определить количество вещества Q,
содержащегося в вертикальном столбе
воды, площадь поперечного сечения
которого равна S
(м2),
а глубина меняется от 0
(м) до L
(м). Концентрация вещества К
(г/м3)
в воде
меняется в зависимости от глубины х
по закону
требуется
определить количество вещества Q,
содержащегося в вертикальном столбе
воды, площадь поперечного сечения
которого равна S
(м2),
а глубина меняется от 0
(м) до L
(м). Концентрация вещества К
(г/м3)
в воде
меняется в зависимости от глубины х
по закону
![]() .
.
-
a
b
L
S
131.
8
0,8
12
2
132.
7
0,7
11
3
133.
6
0,6
10
4
134.
5
0,5
9
2
135.
4
0,4
8
4
136.
8
0,8
16
3
137.
7
0,7
14
2
138.
6
0,6
12
3
139.
5
0,5
10
4
140.
4
0,4
8
2
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА.
Определить количество вещества Q, содержащегося в вертикальном столбе воды, площадь поперечного сечения которого равна 2 (м2), а глубина меняется от 0 (м) до 10 (м). Концентрация вещества К (г/м3) в воде меняется в зависимости от глубины х по закону
![]() .
.
Решение. Рассмотрим бесконечно тонкий слой столба воды с сечением S=2 толщины dx, находящийся на глубине х.
Количество вещества, содержащего в этом слое, равно
![]() .
.
Интегрируя это выражение в пределах от 0 до 10, получим
![]()
![]() (г).
(г).
ТЕМА 10. ФУНКЦИИ МНОГИХ НЕЗАВИСИМЫХ
ПЕРЕМЕННЫХ
В ЗАДАЧАХ 141 - 150 вычислить частные производные первого и второго порядков от заданных функций.
141. ![]() .
.
142. ![]() .
.
143. ![]() .
.
144. ![]() .
.
145. ![]() .
.
146. ![]() .
.
147. ![]() .
.
148. ![]() .
.
149. ![]() .
.
150.
![]() .
.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть
![]() .
.
При
вычислении частной производной
![]() переменную
переменную
![]() рассматриваем как постоянную величину.
Пользуясь правилами дифференцирования
сложной функции, получаем
рассматриваем как постоянную величину.
Пользуясь правилами дифференцирования
сложной функции, получаем
![]() .
.
Аналогично
поступаем при вычислении
![]() .
Считая
.
Считая
![]() постоянной величиной, получаем
постоянной величиной, получаем
![]() .
.
Используя те же правила, вычисляем частные производные второго порядка:
![]() ,
,
![]() (проверьте!),
(проверьте!),
![]() .
.
В ЗАДАЧАХ 151 - 160 исследовать на экстремум заданную функцию.
151. ![]() .
.
152. ![]() .
.
153. ![]() .
.
154. ![]() .
.
155. ![]() .
.
156. ![]() .
.
157. ![]() .
.
158. ![]() .
.
159. ![]() .
.
160. ![]() .
.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть
![]()
Находим частные производные функции:
![]() ;
; ![]() .
.
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки. Для этого решаем систему уравнений:
![]()
откуда
![]() ;
;
![]() .
Таким образом, стационарной является
точка
.
Таким образом, стационарной является
точка![]() .
Находим значения частных производных
второго порядка в точке
.
Находим значения частных производных
второго порядка в точке
![]() :
:
![]() ;
;
![]() ;
; ![]() .
.
Составляем выражение:
![]() .
.
Так
как
![]() и
и
![]() ,
делаем вывод о наличии минимума в точке
.
При этом минимальное значение функции
,
делаем вывод о наличии минимума в точке
.
При этом минимальное значение функции
![]() .
.
ТЕМА 11. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ЗАДАЧАХ 161 - 170 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
-
161. xy2y1 = y2.
162. x2dy+(y2+2)dx = 0.
163. x2dy+(y2+2)dx = 0.
164. xyy2 = 1.
165. ycosx-(y+2)sinx = 0.
166. y (y2+3)ctgx = 0.
167. xyy = 1x2.
168. xyy = (1x2)(1+y2).
169. 2x2yy+y2 = 2.
170. ycos3xy2sin3x = 0.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Найти общее решение дифференциального уравнения
![]() .
.
Решение.
Данное дифференциальное уравнение
относится к типу с разделяющимися
переменными. С учетом того, что
![]() ,
запишем его в виде
,
запишем его в виде
![]() .
.
Разделяем переменные
![]() .
.
Интегрируем обе части равенства и получаем общее решение уравнения:
![]()
Остается вычислить интегралы
![]()
![]()
Таким образом, общее решение дифференциального уравнения имеет вид
![]()
В ЗАДАЧАХ 171 - 180 найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.
-
171.
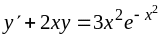 ,
,
 .
.172.
 ,
,
 .
.173.
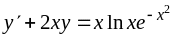 ,
,
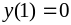 .
.174.
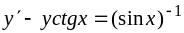 ,
,
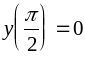 .
.175.
 ,
.
,
.176.
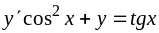 ,
,
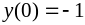 .
.177.
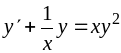 ,
,
 .
.178.
 ,
,
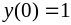 .
.179.
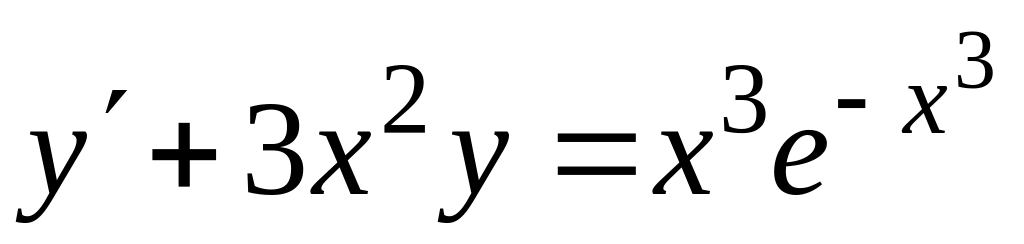 ,
.
,
.180.
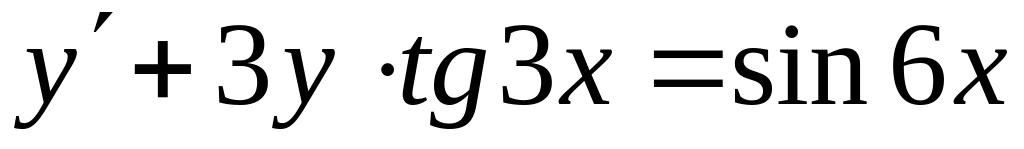 ,
,
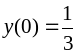 .
.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Найти частное решение дифференциального уравнения
![]() ,
,
удовлетворяющее начальному условию .
Решение.
Заданное дифференциальное уравнение
является уравнением Бернулли. Положим
![]() ,
где
,
где
![]() ,
,![]()
неизвестные функции от
неизвестные функции от
![]() ,
,
![]() .
Подставляя в исходное уравнение вместо
и
.
Подставляя в исходное уравнение вместо
и
![]() соответствующие объекты, будем иметь
соответствующие объекты, будем иметь
![]() ,
,
![]() .
.
Подберем
функцию
![]() так, чтобы выражение, содержащееся в
квадратной скобке, обращалось в нуль.
Тогда для определения
так, чтобы выражение, содержащееся в
квадратной скобке, обращалось в нуль.
Тогда для определения
![]() имеем дифференциальное уравнение с
разделяющимися переменными
имеем дифференциальное уравнение с
разделяющимися переменными
![]() ,
откуда
,
откуда
![]() .
После интегрирования получаем
.
После интегрирования получаем
![]() ,
т.е.
,
т.е.
![]() .
.
Для
определения функции
![]() имеем
имеем
![]()
или
![]() .
.
Это дифференциальное уравнение с разделяющимися переменными относительно неизвестной функции . Разделяя переменные, получаем
![]() .
.
Интегрируя обе части равенства, имеем
![]() .
.
Последний интеграл вычисляем методом интегрирования по частям, в результате чего
![]() ,
,
откуда
![]() .
.
Таким образом, общее решение исходного уравнения имеет вид
![]() .
.
Используя
начальное условие, вычисляем соответствующее
ему значение постоянной
![]() :
:
![]() ,
т.е.
,
т.е.
![]() .
.
Отсюда частное решение исходного дифференциального уравнения, удовлетворяющее заданному начальному условию, имеет вид
![]() .
.
ТЕМА 12. РЯДЫ
В
ЗАДАЧАХ 181 - 200 вычислить
определенный
интеграл с точностью до
![]() путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда.
путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда.
-
181.
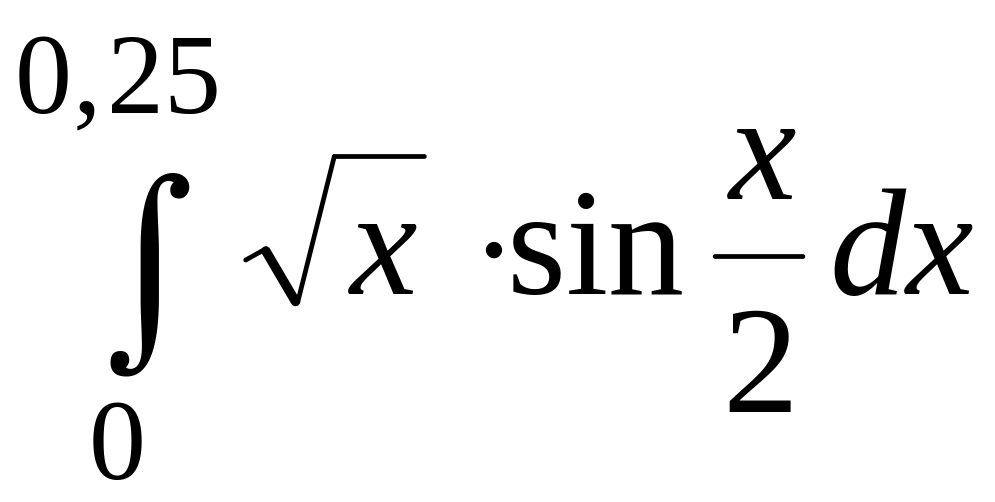 .
.191.
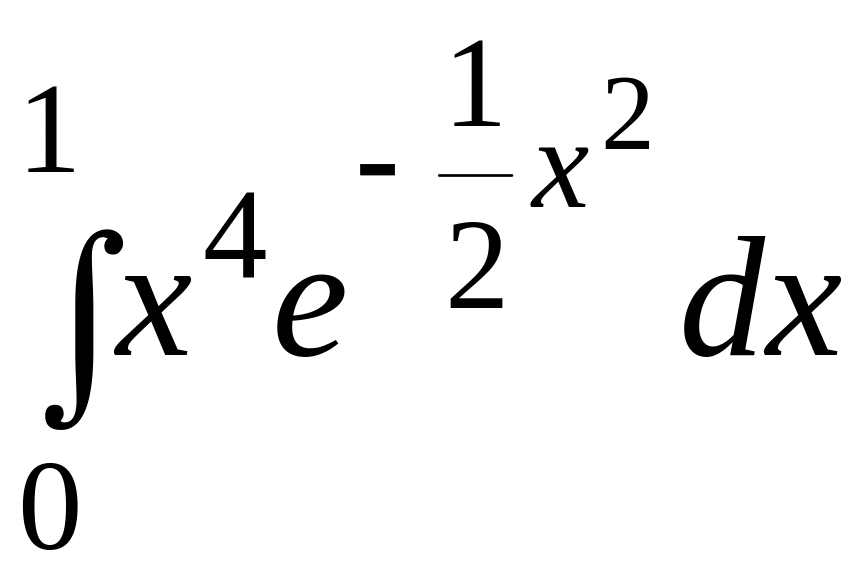 .
.
182.
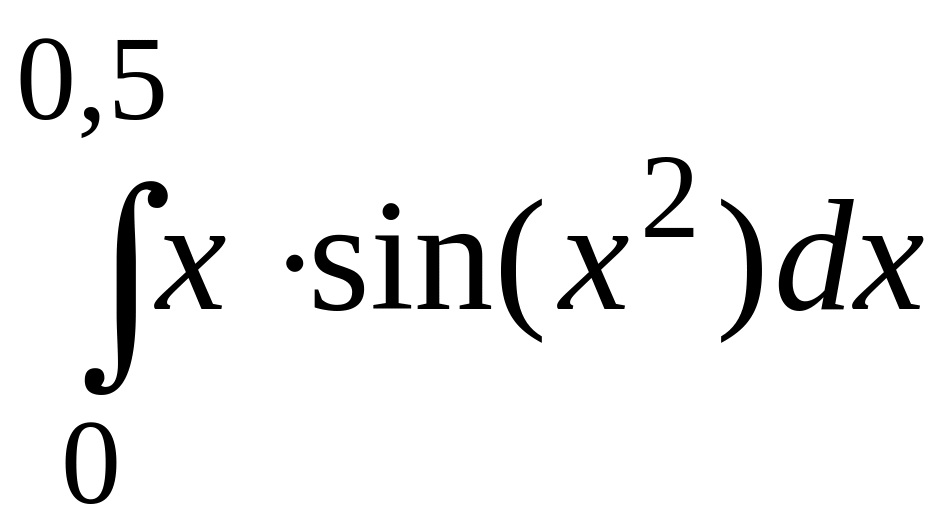 .
.192.
 .
.183.
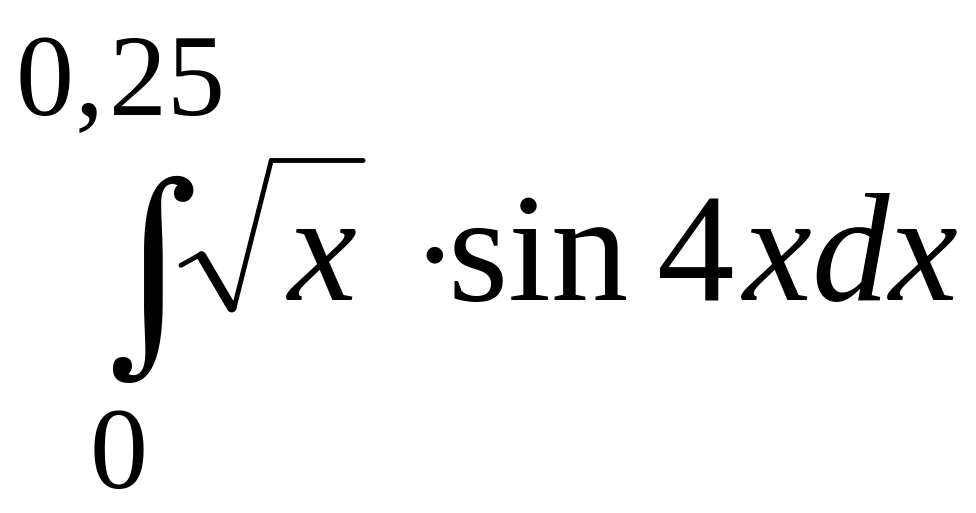 .
.193.
 .
.184.
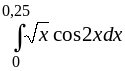 .
.194.
 .
.185.
 .
.195.
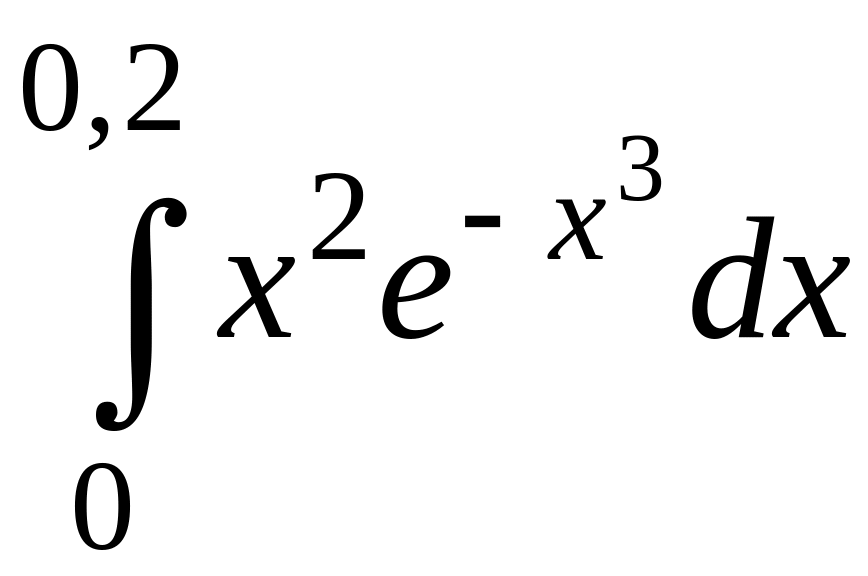 .
.186.
 .
.196.
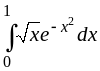 .
.187.
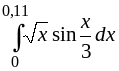 .
.197.
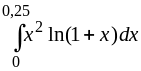 .
.188.
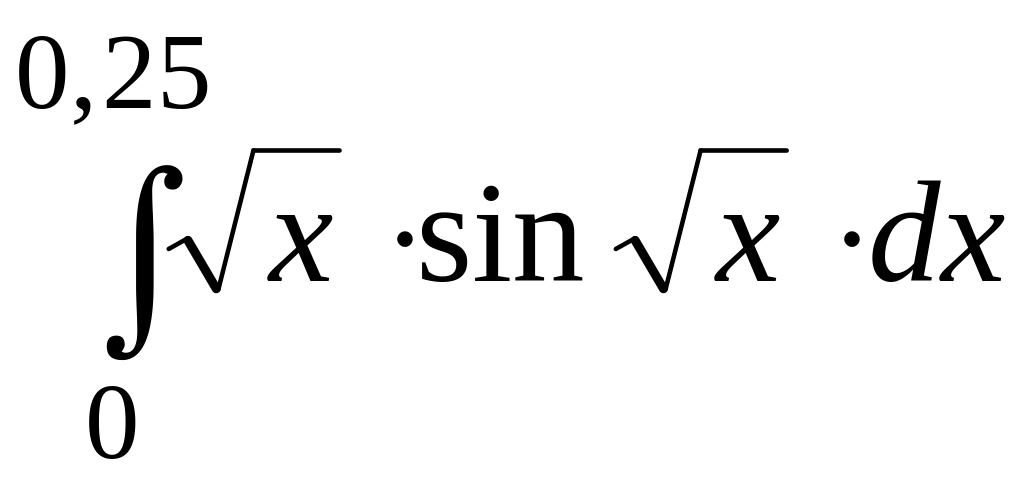 .
.198.
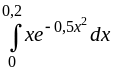 .
.189.
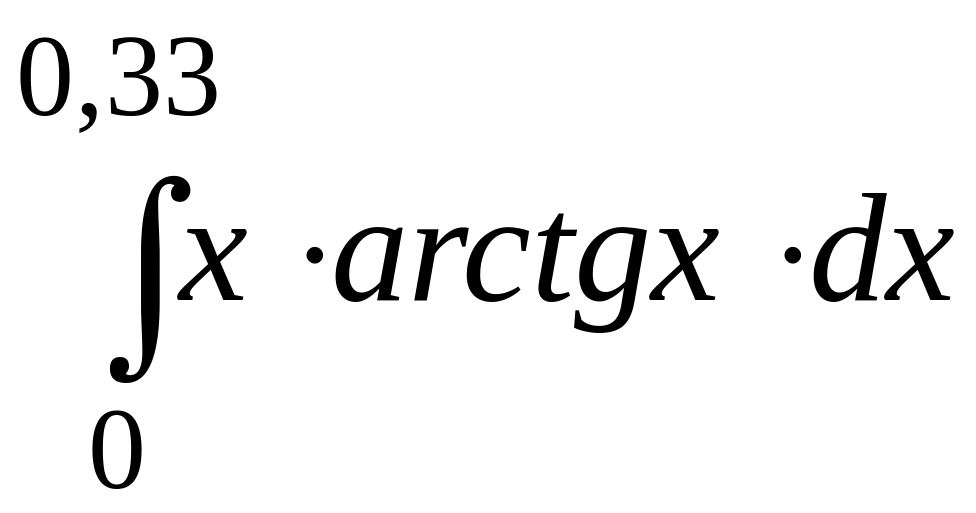 .
.199.
 .
.190.
 .
.200.
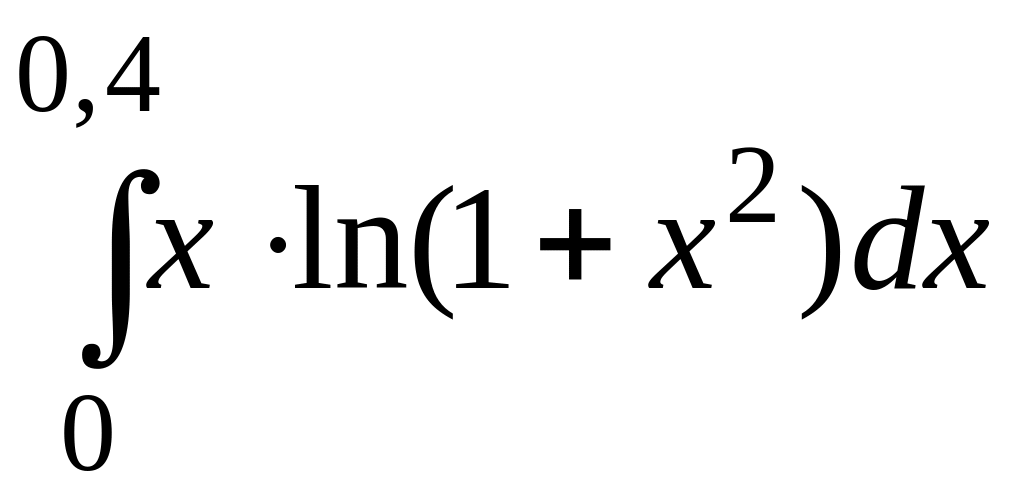 .
.
РЕШЕНИЕ
ТИПОВОГО ПРИМЕРА. Вычислить
с точностью до
![]() интеграл
интеграл
![]()
путем предварительного разложения подынтегральной функции в степенной ряд и почленного интегрирования этого ряда.
Решение.
В разложении функции
![]() в степенной ряд, которое имеет вид
в степенной ряд, которое имеет вид
![]()
![]() ,
,
заменим
на
![]() .
Тогда получим
.
Тогда получим
![]()
Умножая
этот ряд почленно на
![]() ,
будем иметь
,
будем иметь
![]()
