
Тема 3. Векторная алгебра и аналитическая геометрия в пространстве
В ЗАДАЧАХ 21 - 30
даны координаты
вершин пирамиды
![]() .
.
Требуется:
1) записать векторы
![]() ,
,
![]() ,
,
![]() в системе орт
в системе орт
![]() ,
,
![]() ,
,
![]() и найти модули этих векторов; 2) найти
угол между векторами
,
;
3) найти проекцию вектора
на вектор
и найти модули этих векторов; 2) найти
угол между векторами
,
;
3) найти проекцию вектора
на вектор
![]() ;
4) найти площадь грани
;
5) найти объем пирамиды
;
6) составить уравнение ребра
;
4) найти площадь грани
;
5) найти объем пирамиды
;
6) составить уравнение ребра
![]() ;
7) составить уравнение грани
.
;
7) составить уравнение грани
.
21. |
(1; 2; 1), |
(–1; 5; 1), |
(–1; 2; 7), |
|
22. |
(2; 3; 2), |
(0; 6; 2), |
(0; 3; 8), |
(2; 6; 10). |
23. |
(0; 3; 2), |
(–2; 6; 2), |
(–2; 3; 8), |
(0; 6; 10). |
24. |
(2; 1; 2), |
(0; 4; 2), |
(0; 1; 8), |
(2; 4; 10). |
25. |
(2; 3; 0), |
(0; 6; 0), |
(0; 3; 6), |
(2; 6; 8). |
26. |
(2; 2; 1), |
(0; 5; 1), |
(0; 2; 7), |
(2; 5; 9). |
27. |
(1; 3; 1), |
(–1; 6; 1), |
(–1; 3; 7), |
(1; 6; 9). |
28. |
(1; 2; 2), |
(–1; 5; 2), |
(–1; 2; 8), |
(1; 5; 10). |
29. |
(2; 3; 1), |
(0; 6; 1), |
(0; 3; 7), |
(2; 6; 9). |
30. |
(2; 2; 2), |
(0; 5; 2), |
(0; 2; 8), |
(2; 5; 10). |
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть
![]()
1. Известно, что
произвольный вектор
![]() представляется в системе орт
,
,
по формуле
представляется в системе орт
,
,
по формуле
![]() ,
(1)
,
(1)
где
![]() –
координаты вектора
в системе координат
,
порожденной ортами, причем
–
координаты вектора
в системе координат
,
порожденной ортами, причем
![]() .
.
Если заданы точки
![]() и
и
![]() ,
то
,
то
![]() .
.
![]() (2)
(2)
Воспользовавшись формулой (2) и координатами заданных точек, получим
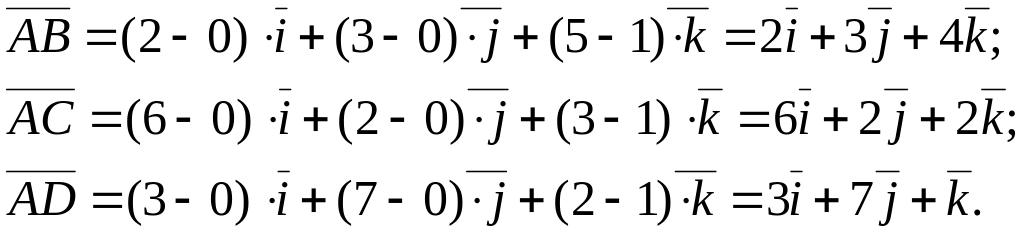
Если вектор
![]() задан формулой (1), то его модуль вычисляется
следующим образом:
задан формулой (1), то его модуль вычисляется
следующим образом:
![]() .
(3)
.
(3)
Используя формулу (3), получаем модули найденных векторов:
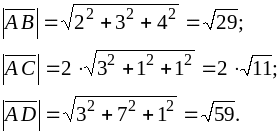
2. Известна формула
![]() ,
,
где
![]() –
скалярное произведение векторов
и
–
скалярное произведение векторов
и
![]() ,
которое можно вычислить следующим
образом:
,
которое можно вычислить следующим
образом:
![]()
У нас
![]()
то есть
![]() .
.
3. Известно, что
![]() ,
,
то есть в нашем случае
![]()
4. Воспользуемся формулой для нахождения площади треугольника, построенного на векторах и ,
![]()
где
![]() –
векторное произведение векторов, которое
можно вычислить по следующему правилу:
–
векторное произведение векторов, которое
можно вычислить по следующему правилу:
 .
.
В нашем примере
![]() ,
причем
,
причем

Таким образом,
![]() (кв. ед.).
(кв. ед.).
5. Объем пирамиды,
построенной на трех некомпланарных
векторах
![]() ,
можно найти по формуле
,
можно найти по формуле
![]() ,
,
где
![]() –
смешанное произведение векторов, которое
вычисляется следующим образом:
–
смешанное произведение векторов, которое
вычисляется следующим образом:
 .
.
У нас
![]() ,
где
,
где
 то
есть
то
есть
![]() (куб. ед.).
(куб. ед.).
6. Известно, что уравнения прямой, проходящей через две заданные точки пространства и , имеют вид
![]() .
(4)
.
(4)
Подставив в (4) координаты точек и , получаем
![]()
то есть уравнение ребра окончательно запишется следующим образом:
![]()
7. Уравнение
плоскости, проходящей через три заданные
точки
![]() ,
можно записать в виде
,
можно записать в виде
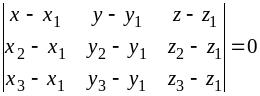 .
.
Подставляя в него координаты точек , получаем

Отсюда
![]()
![]()
![]()
