
m29668_1
.doc
Математическая статистика раздел математики, занимающийся обработкой статистических данных с целью установления закономерностей, присущих массовым случайным явлениям. Исходные статистические данные представляют собой чаще всего сведения о том, какие значения принял в результате наблюдений интересующий нас признак (случайная величина). Методы математической статистики разработаны на основе методов теории вероятностей. Основной метод математической статистики выборочный. Суть его в том, что по сравнительно небольшому количеству статистических данных делаются выводы об особенностях рассматриваемого явления, процесса. Разумеется, эти выводы лишь приближенные оценки вероятностного характера, однако в математической статистике разработаны такие методы сбора и описания выборочных данных, которые позволяют получать по возможности более точные оценки с учетом их надежности.
Математическая статистика возникла в XVI в. и развивалась параллельно с развитием теории вероятностей. В XIXXX вв. большой вклад в становление науки внесли П.Л. Чебышев, А.А. Марков, А.Н. Ляпунов, К. Гаусс, К. Пирсон, А.Н. Колмогоров, Р. Фишер, Ю. Нейман и другие известные ученые-математики.
Тема 1. |
ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ГЕНЕРАЛЬНОГО СРЕДНЕГО. |
Генеральная совокупность – это
большая совокупность однородных
объектов, которую невозможно или
нецелесообразно подвергать сплошному
обследованию. Множество из
![]() объектов, случайным образом отобранных
из генеральной совокупности, называется
выборкой или выборочной совокупностью.
Число
называется объемом выборки. Объем
генеральной совокупности, как правило,
считается бесконечным.
объектов, случайным образом отобранных
из генеральной совокупности, называется
выборкой или выборочной совокупностью.
Число
называется объемом выборки. Объем
генеральной совокупности, как правило,
считается бесконечным.
Например, при диагностике преддиабета важно установить содержание сахара в крови здоровых дюдей. В этом случае все население некоторого региона можно считать генеральной совокупностью, а исследование провести на небольшой группе людей (например, 100-150 чел.) – это и будет выборочная совокупность.
Под репрезентативностью выборки понимают свойство выборочной совокупности достаточно полно и надежно характеризовать генеральную совокупность. Репрезентативность выборки достигается за счет достаточно большого объема выборки, а также благодаря случайному отбору объектов, при котором обеспечивается возможность любого объекта из генеральной совокупности попасть в выборку.
Все хозяйственно-полезные признаки животных подразделяются на количественные и качественные. К качественным признакам животных относятся: пол, окраска шерстяного покрова, тип нервной деятельности, телосложения и др.
Количественные признаки (гематологические и иммунологические показатели крови, живая масса, удой и т.д.) в изучаемой совокупности отличаются высокой степенью изменчивости или, как говорят, варьируют. Изменчивостью принято называть свойство животных отличаться друг от друга в однородной совокупности. В статистике слово «признак» является равносильным понятию «случайная величина» в теории вероятностей.
Результаты наблюдений над признаком
![]() в выборочной совокупности называют
наблюдаемыми значениями или вариантами
в выборочной совокупности называют
наблюдаемыми значениями или вариантами
![]() .
Допустим, например, что при исследовании
плодовитости свиноматок стада были
получены следующие данные о признаке
числе поросят в
помете одной свиноматки:
.
Допустим, например, что при исследовании
плодовитости свиноматок стада были
получены следующие данные о признаке
числе поросят в
помете одной свиноматки:
4, 9, 10, 8 , 7, 9, 11, 12, 5, 6, 10, 8, 8, 9, 11, 9, 6, 7, 5, 7, 6, 9, 8, 11, 9, 8, 10, 9, 10, 6, 9, 8, 10, 9, 9, 8, 7, 10, 9, 9, 7, 6, 9, 9, 10, 9, 8, 9, 10.
Полученная совокупность чисел является
выборкой значений признака
.
Каждое из этих значений признака и есть
варианта
.
Например,
![]() =
4,
=
4,
![]() =
9, … . Поскольку всех значений 50, то объем
выборки
=
50.
=
9, … . Поскольку всех значений 50, то объем
выборки
=
50.
Ряд значений признака, расположенных в порядке возрастания, называется вариационным рядом. Для предыдущей выборки он имеет следующий вид:
4, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 12.
Количество повторений варианты
в вариационном ряду называется частотой
![]() .
Если с учетом этой информации представить
вариационный ряд в виде таблицы, то мы
получим дискретный вариационный ряд:
.
Если с учетом этой информации представить
вариационный ряд в виде таблицы, то мы
получим дискретный вариационный ряд:
-
xi

4
5
6
7
8
9
10
11
12
mi
1
2
5
5
9
16
8
3
1
Здесь в первой строке записаны различные значения (варианты) признака , а во второй строке – соответствующие им частоты, причем сумма частот равна объему выборки:
![]()
Относительной частотой
![]() варианты
называется отношение частоты
к объему выборки:
варианты
называется отношение частоты
к объему выборки:
![]()
Для непрерывного признака строят
интервальный вариационный ряд –
таблицу, в верхней строке которой
записаны классовые интервалы, а в нижней
строке – соответствующие им частоты.
Число классовых интервалов выбирается
в зависимости от объема выборки по
приближенной формуле
![]() .
Длина классового интервала
.
Длина классового интервала
![]() ,
где
,
где
![]() –
размах вариационного ряда.
–
размах вариационного ряда.
В качестве примера рассмотрим интервальный вариационный ряд для признака Х – «процент жира в молоке коровы».
Таблица 1.1
Интервалы значений Х, % |
3,2 – 3,4 |
3,4 –3,6 |
3,6 – 3,8 |
3,8 – 4,0 |
4,0 4,2 |
Частоты mi |
6 |
2 |
4 |
8 |
2 |
Складывая частоты в нижней строке, заключаем, что в таблице приведены результаты обследования по выборке объема n = 22. Среди обследованных коров у шести процент жира в молоке был в пределах от 3,2 % до 3,4 %, у восьми – в пределах от 3,8 % до 4,0 % и т.д.
От интервального ряда можно перейти к дискретному, взяв в качестве вариант значения середин интервалов. Например,
Таблица 1.2
Х, % |
3,3 |
3,5 |
3,7 |
3,9 |
4,1 |
Частоты mi |
6 |
2 |
4 |
8 |
2 |
Соответствие между вариантами вариационного ряда и их частотами (или относительными частотами) принято называть статистическим распределением выборки (или просто распределением выборки). Это соответствие представляют в виде таблицы или графически с помощью полигона или гистограммы.
На рисунке 1.1 построен полигон частот
по данным таблицы 1.2, где точки с
координатами
![]() соединены прямыми линиями.
соединены прямыми линиями.
 mi
8
mi
8


 6
6

 4
4
2 2


33 3,3 3,5 3,7 3,9 4,1 xi
Рис. 1.1. Полигон частот
На рис.1.2 представлена гистограмма частот, построенная по данным таблицы 1.1. Это ступенчатая фигура, состоящая из прямоугольников. Основанием каждого прямоугольника служит некоторый классовый интервал значений признака, расположенный на горизонтальной оси координат. Высота прямоугольника частоты значений признака на соответствующем классовом интервале. Гистограмма позволяет наглядно представить распределение признака в выборке.
mi 8

4 3

 1 2 2
1 2 2
 3,2 3,4 3,6
3,8 4,0 4,2 xi
3,2 3,4 3,6
3,8 4,0 4,2 xi
Рис. 1.2. Гистограмма частот для выборки значений
признака Х – «процент жира в молоке коровы»
Гистограмма
относительных частот представляет
собой ступенчатую фигуру, составленную
из прямоугольников, площадь каждого из
которых равна относительной частоте
вариант, попадающих в интервал, лежащий
в основании прямоугольника. Площадь
этой фигуры равна 1. Если обвести
гистограмму относительных частот
плавной линией так, чтобы площадь,
ограниченная этой линией, и площадь
гистограммы были приблизительно равны,
то полученная кривая будет давать
представление о графике плотности
распределения вероятностей
![]() случайной величины
.
Эта кривая будет тем точнее приближать
график плотности
,
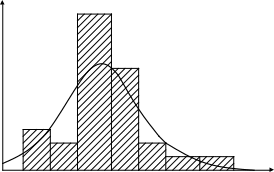
чем больше объем выборки. На рис. 1.3
представлена гистограмма относительных
частот для признака Х – живая масса
коров, кг с наложенной
на нее нормальной кривой. Такое совмещение
на одном чертеже позволяет визуально
оценить близость эмпирического
распределения к нормальному или,
наоборот, нарушение нормального закона.
случайной величины
.
Эта кривая будет тем точнее приближать
график плотности
,
чем больше объем выборки. На рис. 1.3
представлена гистограмма относительных
частот для признака Х – живая масса
коров, кг с наложенной
на нее нормальной кривой. Такое совмещение
на одном чертеже позволяет визуально
оценить близость эмпирического
распределения к нормальному или,
наоборот, нарушение нормального закона.
 wi/
wi/
0 425 450 475 500 525 550 575 600 xi
Рис. 1.3. Гистограмма относительных частот
с наложенной на нее нормальной кривой
Основные выборочные характеристики вычисляются по следующим формулам:
при несгруппированных данных xi:
![]() выборочная (арифметическая) средняя
(
выборочная (арифметическая) средняя
(![]() );
);
![]() выборочная дисперсия;
выборочная дисперсия;
при сгруппированных данных xi: (имеем дискретный ряд)
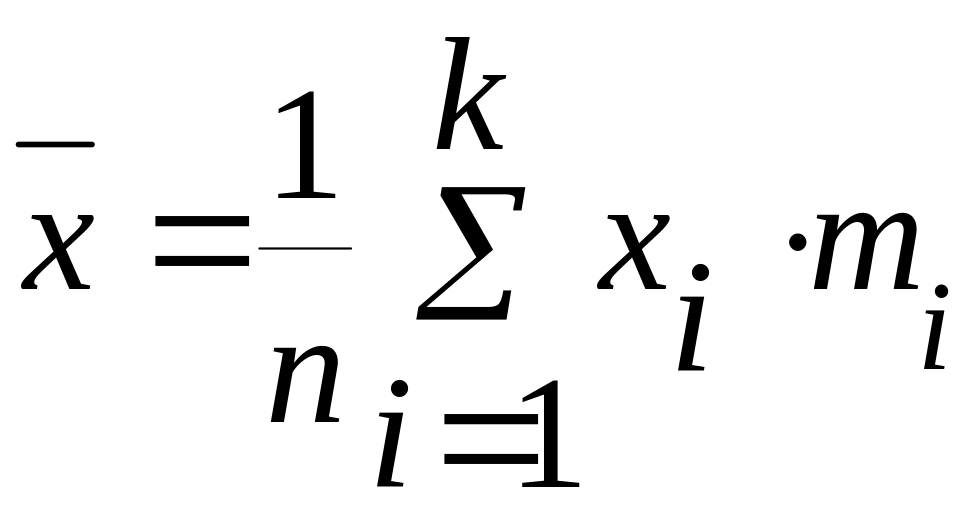
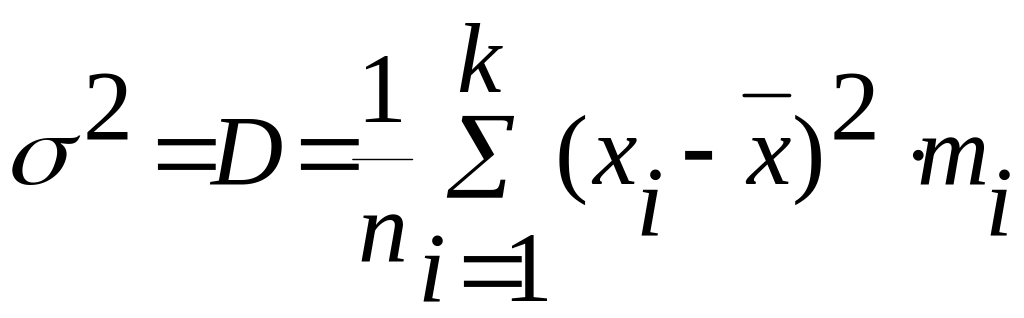
![]() выборочное среднее квадратичное
отклонение (с.к.о.);
выборочное среднее квадратичное
отклонение (с.к.о.);
![]() исправленная выборочная дисперсия;
исправленная выборочная дисперсия;
![]() исправленное выборочное с.к.о.
(стандартное отклонение);
исправленное выборочное с.к.о.
(стандартное отклонение);
![]() ошибка средней арифметической (
ошибка средней арифметической (![]() );
);
![]() (%)
коэффициент
вариации.
(%)
коэффициент
вариации.
Для характеристики степени соответствия
выборочных показателей генеральным
служат величины, называемые ошибками
репрезентативности. Величина
![]() является ошибкой репрезентативности
для выборочной средней, благодаря
которой можно с определенной вероятностью
заключить, с какой точностью
является ошибкой репрезентативности
для выборочной средней, благодаря
которой можно с определенной вероятностью
заключить, с какой точностью
![]() оценивает
генеральное среднее (математическое
ожидание). Следует подчеркнуть, что
ошибки репрезентативности присущи
каждому выборочному показателю и
возникают только оттого, что генеральная
совокупность изучается по своей части
(выборке). В этом смысле ошибки
репрезентативности неустранимы, в
отличие от других ошибок, которые
возможны в исследованиях.
оценивает
генеральное среднее (математическое
ожидание). Следует подчеркнуть, что
ошибки репрезентативности присущи
каждому выборочному показателю и
возникают только оттого, что генеральная
совокупность изучается по своей части
(выборке). В этом смысле ошибки
репрезентативности неустранимы, в
отличие от других ошибок, которые
возможны в исследованиях.
Таблица 1.3
Динамика живой массы ярок, кг
-
Возраст

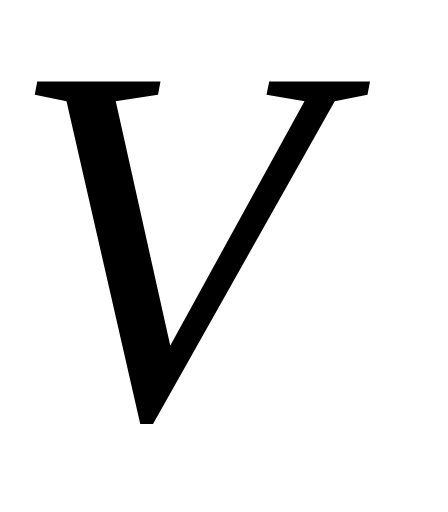
При рождении
50
3,85
 0,06
0,061,75
4,5 мес.
50
20,10 0,35
12,34
14 мес.
50
30,00 0,56
13,39
В научной литературе по биологии и
животноводству данные о выборочной
средней
и ошибке
принято записывать соединенными знаком
![]() :
:
![]() ,
причем вместо
чаще используют обозначение
,
а вместо
обозначение
.
Так, например, из таблицы 1.2 следует, что
для изучения живой массы ярок было
обследовано 50 животных (объем выборки).
При рождении средняя живая масса
составила 3,85 кг, а соответствующая
ошибка
равнялась 0,06.
,
причем вместо
чаще используют обозначение
,
а вместо
обозначение
.
Так, например, из таблицы 1.2 следует, что
для изучения живой массы ярок было
обследовано 50 животных (объем выборки).
При рождении средняя живая масса
составила 3,85 кг, а соответствующая
ошибка
равнялась 0,06.
Дисперсия и среднее квадратичное отклонение характеризуют изменчивость признака. Коэффициент вариации позволяет сравнивать изменчивости признаков, выражаемых в разных единицах измерения (например, высоты и массы). Обычно коэффициент вариации выражают в процентах и наряду с обозначением используют также обозначения v, CV. Изменчивость считается значительной, если коэффициент вариации V>20%, средней, если 10%<V<20%, и незначительной, если V<10%. По данным из таблицы 1.3 можно сказать, что изменчивость живой массы ярок при рождении незначительна, а в дальнейшем повышается.
Пусть признак
распределен в генеральной совокупности
по нормальному закону. Тогда он
характеризуется двумя параметрами a
и
![]() ,
которые в статистике принято называть
генеральными параметрами. Генеральный
параметр a обозначается
также
,
которые в статистике принято называть
генеральными параметрами. Генеральный
параметр a обозначается
также
![]() и называется генеральной средней.
Выборочная средняя
дает приближенное представление о
величине
,
однако более содержательной является
оценка генеральной средней в форме
доверительного интервала
и называется генеральной средней.
Выборочная средняя
дает приближенное представление о
величине
,
однако более содержательной является
оценка генеральной средней в форме
доверительного интервала
![]() ,
,
который с
определенной, наперед заданной
вероятностью
![]() покрывает
.
Крайние точки этого интервала
покрывает
.
Крайние точки этого интервала
![]() (левая граница) и
(левая граница) и
![]() (правая граница) определяют доверительные
границы – крайние значения, минимальное
и максимальное, в пределах которых с
определенной вероятностью
может находиться
.
Вероятность
называется доверительной вероятностью
или надежностью. Величина
(правая граница) определяют доверительные
границы – крайние значения, минимальное
и максимальное, в пределах которых с
определенной вероятностью
может находиться
.
Вероятность
называется доверительной вероятностью
или надежностью. Величина
![]() ,
определяющая доверительные границы,
называется точностью оценки. Как
доказывается в теории интервальных
оценок,
находится из равенства
,
определяющая доверительные границы,
называется точностью оценки. Как
доказывается в теории интервальных
оценок,
находится из равенства
![]() ,
где число
,
где число
![]() называется критерием надежности
Стьюдента и определяется по заданному
уровню значимости
называется критерием надежности
Стьюдента и определяется по заданному
уровню значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() из таблицы критических точек распределения
Стьюдента (приложение 1).
из таблицы критических точек распределения
Стьюдента (приложение 1).
Итак, чтобы установить доверительный интервал для генеральной средней, необходимо:
найти выборочную среднюю ;
найти ошибку средней ;
по заданной надежности определить уровень значимости и с учетом числа степеней свободы
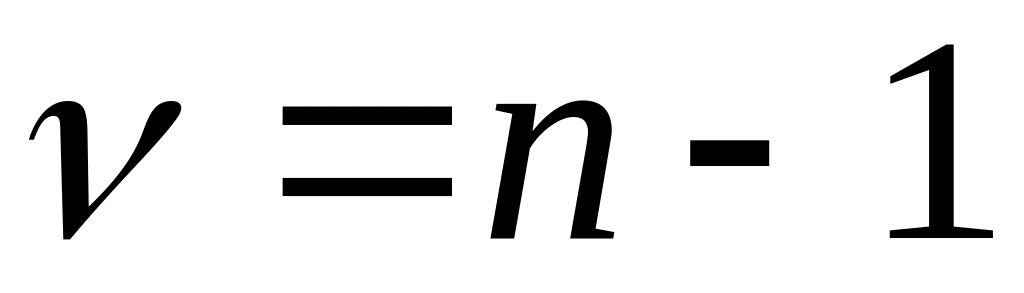 найти критерий надежности
найти критерий надежности
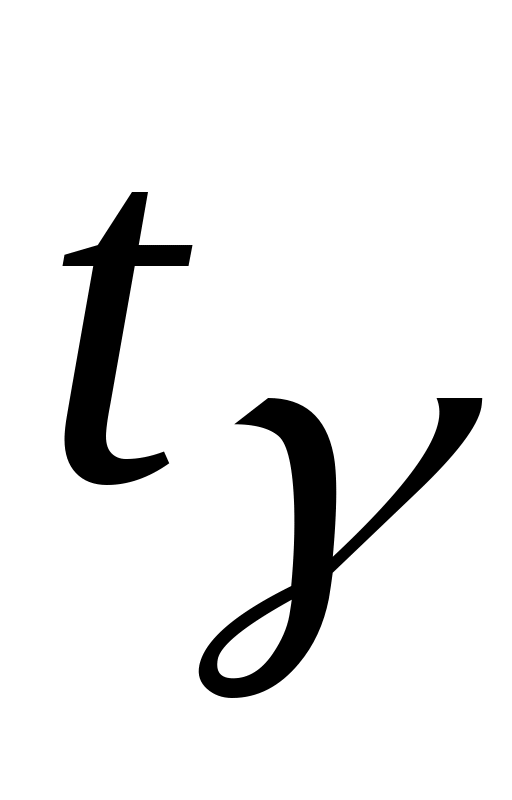 ;
;найти точность оценки ;
найти доверительные границы и ;
записать доверительный интервал
.
ПРИМЕР
Из большого стада коров произведена случайная выборка, в результате обследования получено 20 вариант живой массы (кг) коров:
xmax
541, 534, 526, 523, 526, 527, 526, 546, 540, 526,
532, 521, 532, 536, 521, 510, 534, 520, 527, 532.
xmin
I. Преобразуем выборку. Для этого отметим, что наименьшее значение признака Х – «живая масса коров» равно 510 кг, а наибольшее значение 546 кг (эти числа называют лимитами). Размах вариационного ряда 546 - 510 = 36 кг. Запишем исходные данные в виде ранжированного вариационного ряда:
510, 520, 521, 521, 523, 526, 526, 526, 526, 527,
527, 532, 532, 532, 534, 534, 536, 540, 541, 546.
При данном объеме выборки (20 вариант) наметим 5 классов. Увеличив в нашем примере размах вариационного ряда до 40, мы можем взять длину Δ классового интервала равной 8 кг, в результате чего получим пять интервалов:
510-518, 518-526, 526-534, 534-542, 542-550.
Теперь определим частоты попадания вариант выборки в каждый классовый интервал (варианту, попавшую на границу двух соседних классовых интервалов, отнесем в предыдущий из них) и получим интервальный вариационный ряд:
Интервалы значений признака X, кг |
510-518 |
518-526 |
526-534 |
534-542 |
542-550 |
Частоты mi |
1 |
8 |
7 |
3 |
1 |
Дополним интервальный вариационный ряд строкой относительных частот wi и строкой плотностей ρi , проводя вычисления по формулам
![]() ,
ρi =
wi
/
Δ:
,
ρi =
wi
/
Δ:
w1 = m1/n = 1/20; |
1 = w1 / Δ = 1/160; |
w2 = m2/n = 8/20; |
2 = w2 / Δ = 8/160; |
w3 = m3/n = 7/20; |
3 = w3 / Δ = 7/160; |
w4 = m4/n = 3/20; |
4 = w4 / Δ = 3/160; |
w5 = m5/n = 1/20; |
5 = w5 / Δ = 1/160. |
Для контроля вычислений проверяем выполнение условий «сумма частот равна объему выборки»:
![]() ,
,
и «сумма относительных частот равна единице»:
![]()
![]()
В результате получаем таблицу 1.4.
Таблица 1.4
Интервальный вариационный ряд для выборки значений
признака Х «живая масса коров», относительные частоты
вариант и их плотности
Интервалы значений признака X, кг |
510-518 |
518-526 |
526-534 |
534-542 |
542-550 |
Частоты mi |
1 |
8 |
7 |
3 |
1 |
продолжение |
|||||
Относительные частоты wi |
1/20 |
8/20 |
7/20 |
3/20 |
1/20 |
Плотности относительных частот i |
1/160 |
8/160 |
7/160 |
3/160 |
1/160
|
Построим гистограмму относительных частот, используя ее определение и данные, расположенные в первой и четвертой строках таблицы 1.4.
