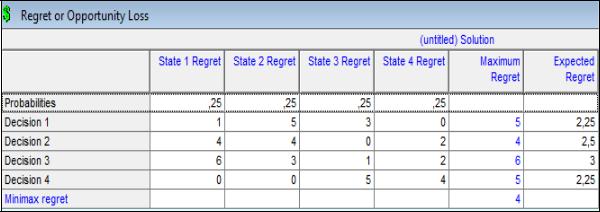
Рисунок 4.7 – Окно отчёта о вычислении критерия минимаксного риска Сэвиджа

На рисунке 4.7 показаны расчёты критерия минимаксного риска Сэвиджа (он равен 4 и реализован второй альтернативой).

4.5. Задания к выполнению лабораторной работы №4

Необходимо выполнить анализ всех задач, описанных в этом разделе. Исходную информацию для выполнения лабораторной работы возьмёте из

задания по транспортной задаче. Игра должна быть 4х4. Матрица транспортных расходов – это три стратегии игрока А. Четвёртую стратегию этого игрока составит строка потребностей (последняя строка, не включённая в матрицу транспортных расходов).

Для решения задачи графическим методов выберите две активные стратегии игрока А с минимальными частотами.

Для анализа игры с природой возьмите эту же платёжную матрицу.

5. Лабораторная работа №5

Системы массового обслуживания

5.1. Общие сведения

Существует широкий класс задач, с которыми приходится постоянно сталкиваться в повседневной и хозяйственной деятельности, где имеют место процессы, приводящие к задержкам в обслуживании и очередям. Системы, в которых протекают указанные процессы, получили название систем массового обслуживания (МО), а математическим описанием или разработкой математических моделей процессов, протекающих в них, занимается теория МО.

51

В процессе изучения очередей сначала необходимо обращать внимание на следующие основные её компоненты: входящий поток требований, каналы обслуживания, наличие очереди и выходящий поток. Эти составляющие не требуют разъяснения, за исключением дисциплины очереди. Последнее – это просто правило обслуживания. В дальнейшем мы будем рассматривать правило: первый пришёл, первый обслуживается. Системы МО связаны с двумя видами издержек: издержки обслуживания, увеличивающиеся при повышении уровня обслуживания, и издержки, связанные с ожиданием, уменьшающиеся с увеличением уровня обслуживания. Как известно, существует точка минимума общих издержек системы МО.

Определение оптимального уровня обслуживания, минимизирующего суммарные издержки системы МО, и является одной из основных задач при разработке и эксплуатации систем МО.

5.2. Основные характеристики систем массового обслуживания

Входящий поток – это поток требований, нуждающихся в обслуживании и поступающих в обслуживающую систему. Поток требований может быть детерминированным или случайным. Детерминированный поток предполагает, что заявки в систему МО поступают через равные промежутки времени. Случайный поток требований предполагает, что требования в систему МО прибывают случайно, так что их поступления нельзя предсказать точно, но можно оценить на основе известного закона распределения вероятностей.

Для математического описания процесса поступления заявок в систему МО обычно применяется аппарат, разработанный для марковских случайных процессов. В марковских случайных процессах будущее развитие системы зависит только от настоящего состояния и не зависит от предыстории процесса. Кроме того, в дальнейшем будем предполагать, что поступления заявок в систему МО описывается случайным процессом с дискретным состоянием, т.е. возможные состояния системы можно перенумеровать, а переход системы из одного состояния в другое происходит скачком (мгновенно), в случайные моменты времени. Можно показать, что вероятности состояний для системы МО в этих предпосылках могут быть описаны распределением Пуассона. Пусть r – число прибытий требований в систему МО в единицу времени (мин, час, сутки и т.д.). Тогда вероятность того, что в системе МО будет находиться r требований, будет равна

52

где λ – среднее число требований, прибывающих в систему за единицу времени или средняя интенсивность входящего потока;

1/ λ – среднее время между заявками.

Как известно, распределение Пуассона – это дискретное распределение, для которого математическое ожидание и дисперсия совпадают и равны λ, т.е. а = σ2 = λ.

Выходящий поток – это поток требований, покидающий обслуживающую систему. Процесс обслуживания заявок зависит от свойства и типа системы МО, в том числе, подобно характеру прибытия, этот процесс может быть детерминированным или случайным.

Во многих случаях предполагается, что случайное время обслуживания описывается отрицательным экспоненциальным или показательным распределением вероятностей. Известно, что это предположение математически оправдано, если интенсивность входящего потока описывается пуассоновским распределением. В отличие от последнего показательное распределение является непрерывная и имеет вид:

P (T > t) = e - μ t, для t ≥ 0,

где P (Т > t) – вероятность того, что время обслуживания будет больше t; μ – средняя интенсивность обслуживания; 1/μ – среднее время обслуживания.

Величина μ называется параметром показательного закона распределения. Известно, что а = σ = 1/μ.

Для многофазных систем МО выходящий поток описывается распределение Эрланга с функцией плотности распределения

В многофазной системе МО предполагается, что все k фаз имеют одинаковое экспоненциальное распределение времени обслуживания со средним, равным 1/kμ , а объединённая функция распределения имеет среднее, равное 1/μ и дисперсию 1/kμ2.

53

Системы МО подразделяются на системы с бесконечной очередью и с конечной очередью. В зависимости от этого, операционные характеристики системы МО рассчитываются исходя из разных соотношений. Трудно себе представить реальную систему МО с бесконечной очередью, но, учитывая простоту их математического описания, здесь они будут рассмотрены. Более реальны системы МО с ограниченной очередью. Очередь может быть ограничена либо наличием свободных мест, либо временем ожидания.

Системы МО различаются мощностью источника заявок. Размер источника заявок может быть конечным и бесконечным. Например, источник, формирующий заявки на обслуживание посетителей в магазине, парикмахерской можно считать практически бесконечным. В этом случае поступившая заявка никак не повлияет на вероятность появления очередной заявки. В противном случае (источник конечной емкости) поступление очередной заявки снижает частоту поступления очередных заявок. Такие системы называются замкнутыми системами МО.

5.3. Модели массового обслуживания

Для классификации моделей массового обслуживания будем пользоваться обозначениями, введёнными Кендаллом. В соответствии с этими обозначениями для характеристики модели массового обслуживания достаточно указать значения шести параметров в следующем формате: (закон распределения для входящего потока / закон распределения длительности обслуживания / число каналов обслуживания): (дисциплина очереди / максимальная длина очереди / ёмкость источника, генерирующего заявки на обслуживание).

Обычно принимаются следующие обозначения для закона распределения входящего потока:

М – пуассоновское (марковский случайный процесс);

Д– детерминированный (с фиксированным интервалом времени между моментами последовательных поступлений заявок в систему);

Еk – Эрланга с параметром k; G – произвольное.

Для обозначения закона распределения времени обслуживания обозначения следующие:

М – отрицательный экспоненциальный;

Д– детерминированный (с фиксированной продолжительностью обслуживания);

54

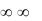
Еk – Эрланга с параметром k;

GS – общее распределение произвольного вида.

Для рассматриваемых далее моделей массового обслуживания дисциплина очереди принимается естественной: первый пришёл, первый обслуживается и она обозначается FCFS.

Например, обозначения (Д/Д/1):(FCFS/ / ) означают, что мы имеем дело с моделью массового обслуживания, в которой детерминированный входящий поток, один канал обслуживания, естественная дисциплина очереди, неограниченная длина очереди и неограниченная ёмкость источника заявок. Для теории массового обслуживания подобная модель не представляет интереса и здесь рассматриваться не будет. Кроме того, обычно последний блок обозначений считается стандартным и часто не указывается; он подключается в случае, если вводятся ограничения либо на длину очереди, либо на ёмкость источника заявок.

Рассмотрим несколько частных стандартных случаев моделей массового обслуживания и приведём формулы для расчёта операционных характеристик таких моделей, имея в виду, что при необходимости эти характеристики могут быть использованы для расчёта стоимостных показателей функционирования систем массового обслуживания и выбора оптимальных стратегий управления этими системами, выбирая уровень обслуживания и издержки системы.

Модель 1: (М/М/1) – Одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и экспоненциальным временем обслуживания.

Предпосылки модели. Одноканальная однофазная модель массового обслуживания с такими характеристиками является одной из наиболее часто используемых и простых моделей. Она является базовой моделью, поэтому рассмотрим её подробно. Обычно она используется при выполнении следующих семи предпосылок:

1)требования обслуживаются в порядке FCFS;

2)каждое требование дожидается обслуживания, несмотря на длину очереди (система массового обслуживания без отказов);

3)требования поступают в систему независимо друг от друга, случайным образом, с известной (фиксированной в среднем) интенсивностью;

4)закон распределения числа требований, прибывающих в систему за

единицу времени, является пуассоновским, и ёмкость источника

55

требований не ограничена (требования поступают из неограниченной совокупности);

5)время обслуживания требований случайное, не меняется от требования к требованию, средняя же интенсивность обслуживания известна;

6)время обслуживания требований подчинено экспоненциальному закону распределения;

7)средняя интенсивность обслуживания больше, чем средняя интенсивность прибытия.

Последнее требование обязательно для устойчивого функционирования системы массового обслуживания ибо, в противном случае, очередь будет неограниченно возрастать.

5)коэффициент использования времени обслуживания системы, т.е. вероятность того, что система занята обслуживанием

=/ ;

6)вероятность простоя системы массового обслуживания, т.е. вероятность того, что в системе нет ни одного требования

Р0 = 1– / ;

7) вероятность того, что в системе находится n требований Рn = ( / )n (1– / );

8) вероятность того, что в системе находится не менее k требований Рn k = ( / )k .

Кроме того, приведём формулы, позволяющие выразить одну из указанных величин через другую, что упрощает иногда их вычисление:

56

обслуживания с пуассоновским входящим потоком и произвольным распределением интенсивности обслуживания.

В отличие от предыдущей модели здесь предполагается, что закон распределения времени обслуживания неизвестен, но известно среднее время

L = Lq + / ; Wq = Lq / ; W = Wq + 1/ .

Модель 3: (М/D/1) – одноканальная однофазная модель с пуассоновским входящим потоком и фиксированным временем обслуживания. От предыдущей модели эта модель отличается лишь тем, что для неё =0.

Модель 4: (М/Еk/1) – одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и выходящим потоком Эрланга (k фаз).

Эта модель также является частным случаем модели 2 при

Не следует забывать, что, как это было указано при обсуждении закона распределения Эрланга, время обслуживания для каждой фазы считается одинаковым, а общее время обслуживания в системе кратно числу фаз. Например, если время обслуживания для каждой фазы равно 10 минут, а число фаз k=3, то общее время обслуживания равно 30 минут, т.е. интенсивность обслуживания в среднем равна двум требованиям в час (т.е. =2).

Модель 5: (М/М/S) – в отличие от модели 1 здесь предполагается, что система массового обслуживания имеет s каналов обслуживания. Интенсивность каждого канала обслуживания одинакова и равна , так что суммарная интенсивность системы массового обслуживания равна s 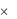. Следовательно, для

57

устойчивого функционирования системы необходимо, чтобы s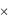 было больше интенсивности входящего потока .

Операционные характеристики такой системы определятся из соотношений:

L = Lq + / ; Wq = Lq / ; W = Wq + / . Модель 6: (M/M/1) : (FCFS /m/ )

От модели 1 эту модель отличает то, что здесь введены ограничения на длину очереди: m – максимальное число требований в системе, следовательно, если в системе заняты все m мест, то очередное требование покинет систему необслуженным. Такая система массового обслуживания называется системой с отказами. Операционные характеристики такой системы определятся из соотношений

Рm – вероятность того, что требование покинет систему необслуженным.

Модель 7: (М/М/1):(FCFS/ /m)

В этой модели в отличие от модели 1 предполагается, что ёмкость источника заявок ограничена величиной m. Такие системы массового обслуживания

В программе QM в модуле Waiting Lines – линии ожидания или в другой терминологии – система массового обслуживания приводится 9 моделей таких систем в следующих обозначениях:

Вышеописанные модели соответствуют этому списку, кроме модели 7, которая в этом списке обозначена как модель 8. Модели 7 и 8 из этого списка здесь не описаны.

Следует отметить, что система МО будет функционировать устойчиво, если интенсивность поступления заявок меньше интенсивности обслуживания. В противном случае очередь будет расти до бесконечности, и в таких ситуациях программа выдаёт предупреждение

- ошибка в данных: интенсивность обслуживания должна быть строго меньше, чем интенсивность прибытия. В таком случае, щёлкнув по кнопке ОК,

исправьте данные.

59

5.4. Пример использования этих моделей

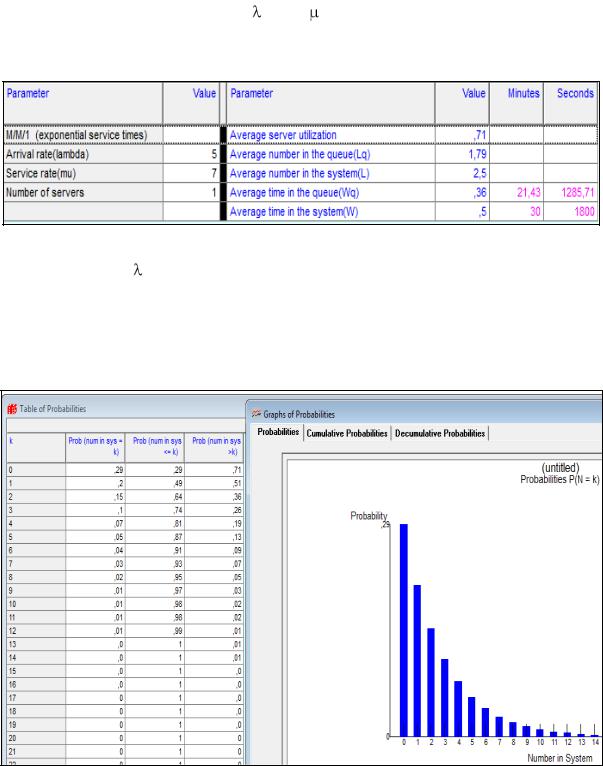
Пусть имеем первую модель и = 5, а = 7.

Выбрав модель 1, заполним исходные данные и решим задачу(рисунок 5.1).

Рисунок 5.1 – Исходные данные и решение задачи Итак, 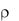= /= 0,71 – первая строка отчёта – средняя интенсивность

использования системы, т.е. вероятность того, что система занята обслуживанием, а остальные операционные характеристики этой СМО соответствуют ранее введённым обозначениям. Кроме того, можно вывести вероятности нахождения системы в том или ином состоянии (рисунок 5.2).

Рисунок 5.2 – Вероятностные характеристики системы

Так, например, P0 = 0,29; P1 = 0,2 и т.д., что отражено в первом столбике таблицы вероятностей и на графике. Второй столбик вероятностей – это вероятности, что в системе будет находиться не менее k требований, а третий – более k требований.

60

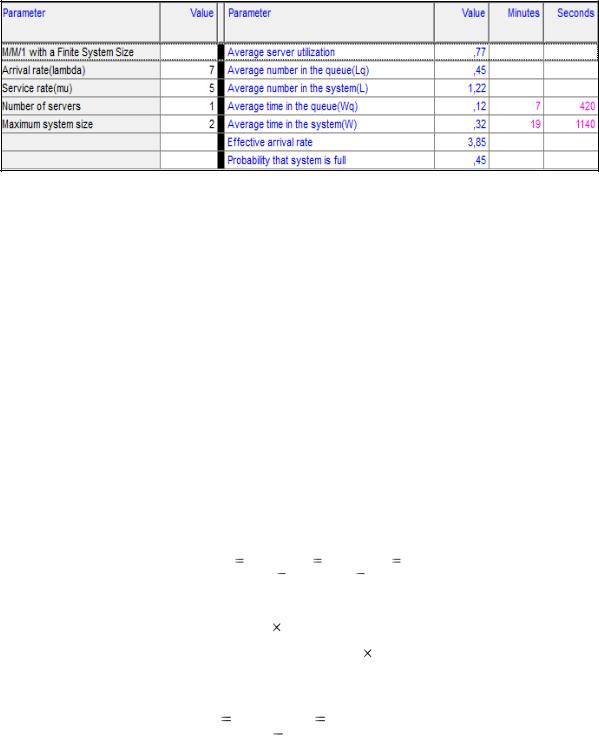
Если предположить, что в СМО может находиться только два требования, то при тех же данных операционные характеристики системы изменятся (например, одна бензоколонка и на ней могут находиться только два автомобиля) (рисунок

5.3):

Рисунок 5.3 – Решение задачи по модели (М/М/1)

В заключение приведём пример использования стоимостных показателей при анализе систем МО.

Пусть имеется система МО типа (М/М/1) с λ = 2 и μ = 3 и издержки ожидания в очереди равны 60 руб. за час, а издержки функционирования равны 42 руб. за час. Кроме того, имеется аналогичная система МО с большей интенсивностью обслуживания (μ = 4), но и большими издержками обслуживания (54 руб. за час). Необходимо выбрать из них более эффективную, предполагая, что общие издержки систем состоят из издержек обслуживания и ожидания исходя из 8-часового рабочего дня.

Подсчитаем издержки функционирования каждой системы. В первой системе – 42*8 = 336 (руб.), во второй – 54*8 = 432 (руб.).

Далее, используя модель 1, определим среднее время ожидания требований в системе и соответствующие ему издержки ожидания.

16*1/4 = 4 (часа), а издержки 4*60 = 240 (руб.).

Итак, общие издержки в первой системе равны 336 + 640 = 976 (руб.), а во второй – 432 + 240 = 672 (руб.), т.е. вторая система МО более эффективна.

61

Предположим далее, что появилась возможность организовать второй канал обслуживания с теми же характеристиками, что в первом случае. Будет ли это выгодно, по сравнению со вторым случаем?

Издержки функционирования такой системы определяются как 42*8*2 = 672 (руб.). Из модели 5 определим Wq = 0,041 5 часа или среднее время ожидания 0,0415*16 = 0,066 4 (часа).

Тогда издержки ожидания равны 60*0,664 = 39,84 (руб.), а общие издержки: 672 + 39,84 = 711, 84 (руб.).

Сравнивая с 672 руб., видим, что второй случай более выгоден.

5.5. Задания для выполнения лабораторной работы №5

Считать, что интенсивность входящего потока равна 10+n, где n – номер варианта;

интенсивность потока обслуживания равна 15+n;

число каналов обслуживания равно 2 (в этом случае интенсивность входящего потока удваивается);

число фаз равно 2 (в этом случае интенсивность потока обслуживания удваивается);

число мест в очереди равно 2; ёмкость источника заявок равна 3.

Решите задачу выбора оптимальной СМО со своими данными при этом подключите позицию «Use costs».

6.Лабораторная работа № 6

Сетевое моделирование

6.1.Решение задач из модуля Networks

Рассмотрим сначала решение трёх простейших задач из раздела сетевые модели. Они реализованы в программе QM в модуле Networks.

В этом модуле предполагается решение трёх частных задач, объединяет которые то, что все они могут быть представлены схематично в виде сети дорог, коммуникаций и т. п. Создавая файл исходных данных, вы получаете возможность выбрать ту или иную задачу из списка задач:

Соответствующий список задач следующий:

62

минимизация дерева расстояний;

определение кратчайшего пути;

определение максимального потока. Рассмотрим их последовательно.

6.1.1. Минимизация дерева расстояний предполагает определение кратчайшей общей длительности пути, соединяющего все пункты сети друг с другом. Примером такой задачи может служить задача по определению минимального расхода провода для соединения всех пунктов сети с центральным телефонным узлом или для создания компьютерной кабельной сети с центральным сервером.

Алгоритм решения такой задачи предполагает реализацию трёх пунктов:

1.Произвольно выбирается узел сети, который соединяется с узлом сети с кратчайшим расстоянием до него.

2.Выбранные узлы образуют множество соединённых узлов, а остальные – множество несоединённых узлов. Определяем узел несоединённого множества с кратчайшим расстоянием до соединённого множества. Соединяем эти два узла.

Вслучае нескольких равных кратчайших расстояний выбираем для соединения любой из этих узлов.

3.Если все узлы сети соединены, то решение заканчиваем, в противном случае переходим к пункту 2.

Рассмотрим пример. Пусть дана сеть:

Рисунок 6.1 – Схема дорог для задачи минимизации дерева расстояний

Поместим данные этой задачи в окно исходных данных программы. Нумерацию пунктов будем вести в соответствии с рисунком 6.1. Зададим число

63

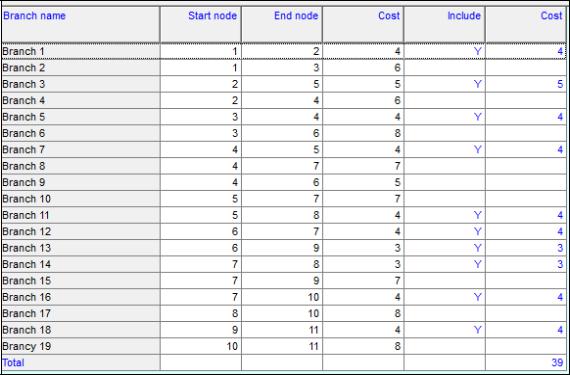
дуг сети, равное 19, и введём в таблицу исходные данные. Получим после решения:

Рисунок 6.2 – Окно исходных данных и решение задачи минимизации дерева расстояний

В этом окне помечены ветви, вошедшие в решение задачи. Если соединить узлы сети по этим ветвям, то получим минимальный расход провода, равный 39 единиц.

6.1.2. Задача определения кратчайшего пути в сети соответствует своему названию и определяет кратчайший путь от исходного узла сети до завершающего, если не указывать, откуда и куда необходимо двигаться. Алгоритм решения такой задачи состоит из пяти пунктов.

1.Начальный узел сети определяем как элемент постоянного множества и затем определяем смежные с ним узлы.

2.Определяем среди смежных узлов узел с кратчайшим расстоянием до какого либо узла постоянного множества.

3.Фиксируем эту ветвь и вычёркиваем другие ветви, соединяющие элементы постоянного множества с выбранным узлом смежного множества, но имеющие большую длину.

4.Присоединяем выбранный узел к элементам постоянного множества.

5.Определяем новое смежное множество узлов. Если такового нет, то решение заканчиваем, в противном случае переходим к пункту 2.

64

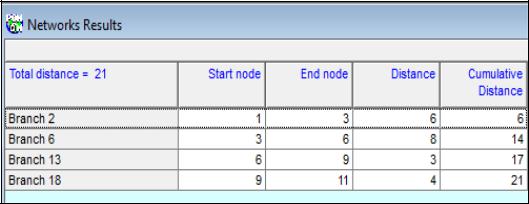
Проиллюстрируем работу алгоритма на этом же примере (рисунок 6.1). Введём число ветвей, равное 19, и остальные установки по умолчанию. После ввода информации и решения задачи получим следующие результаты (рисунок

6.3):

Рисунок 6.3 – Окно решения задачи определения кратчайшего пути в сети Как видим, кратчайший путь от первого до 11-го узлов проходит через узлы 1

– 3 – 6 – 9 – 11 и равен по длине 21 единице.

Кроме того, при необходимости можно вывести на экран или на принтер окно

сматрицей расстояний между всеми пунктами сети.

6.1.3.Задача определения максимального потока в сети позволяет определить максимальную пропускную способность сети, например, при перекачке нефти по системе трубопроводов, воды по системе ирригационных каналов, пропуске электроэнергии по системе линий передач и т. д. При формулировке задач такого типа необходимо указывать пропускную способность каждой ветви в обоих направлениях.

Алгоритм решения такой задачи состоит из трёх пунктов.

1.Определяем произвольный путь от начального узла сети к конечному с положительной пропускной способностью для каждой ветви этого пути. Если такового нет, процесс решения заканчивается.

2.Определяем в выбранном пути ветвь с минимальным потоком. Эту минимальную величину обозначим через с и припишем каждой ветви выбранного пути.

3.Уменьшим пропускную способность текущего потока для каждой ветви выбранного пути на величину с в прямом направлении и увеличим в противоположном. Последнее позволяет определить потенциальную возможность для каждой ветви сети. Затем переходим к пункту 1.

65