
Красников Моделирование физических процессов с исползованием 2012
.pdf3.10.Формы уравнений
3.10.1.Общие сведения
Одним из ключевых моментов моделирования в FEMLAB является форма уравнения. Системы уравнений, используемые в расчётах моделей, обязательно принимают одну из следующих форм.
1.Коэффициентная форма. Уравнение задаётся в виде коэффициентов при производных разного порядка, заданных прикладным режимом величин. Данная форма используется в основном для линейных уравнений.
2.Генеральная форма. Уравнение задаётся в свободном виде. Используется для нелинейных уравнений.
3.Слабая форма. Задаётся не само уравнение, а интегральное приближение в формуле (1.3). Эта форма – прямое использование метода конечных элементов
Все системы уравнений, на которых основаны прикладные режимы в FEMLAB обязательно принимают какую-либо из вышеперечисленных форм (как правило, генеральную, или коэффициентную). Посмотреть, в какую форму имеет данное уравнение, а также поменять её, можно вызвав пункт меню Physics->Model Settings в пункте Equation system form. При этом задачу в коэффициентной форме можно привести к генеральной, или слабой, но не наоборот. Если для режима теплопроводности доступны все три формы, то для режима уравнений гидродинамики, как для нелинейной системы, коэффициентная форма недоступна.
3.10.2. Прикладные режимы
Ранее, было изучено, что основным фундаментальным моментом в FEMLAB является выбор нужного прикладного режима. Помимо прикладных режимов, связанных с какими-либо конкретными системами уравнений, в навигаторе моделей имеется возможность задавать систему дифференциальных уравнений в частных производных в общем виде какой-нибудь формы. В таких режимах можно решать любые дифференциальные уравнения путём приведения системы к необходимому виду. Часто подобный метод при-
131
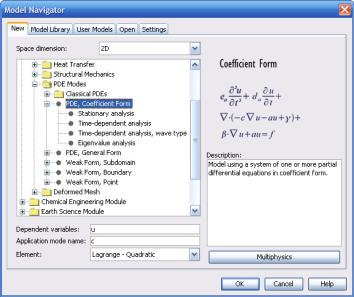
даёт дополнительную гибкость в постановке задачи и более предпочтителен, чем выбор какого-либо прикладного режима. Уравнения в различных формах доступны в разделе Comsol Multiphysics- >PDE Modes (рис. 3.77).
Рис. 3.77. Прикладные режимы уравнений в разных формах.
PDE, Coefficient form – коэффициентная форма уравнения. Доступны стационарный, нестационарный режимы, волновой тип уравнения, задача на собственные значения.
PDE, General form – генеральная форма уравнения. Подразделы аналогичны предыдущему пункту.
Weak form – слабая форма уравнения. Доступны три различных типа задания форм для разных уровней областей: для области, границы, точек (в трёхмерном случае также доступна слабая форма для пространства).
Далее рассмотрим каждую из них более подробно.
132

3.10.3. Коэффициентная форма уравнения
Общий вид коэффициентной формы уравнения:
c |
|
∂2u |
+ d |
|
∂u |
+ (− cu − αu + γ)+ β u + au = |
|
||||
a |
a |
f |
; |
||||||||
|
∂t2 |
|
∂t |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Ω |
||
n(c u |
+ αu − γ)+ qu = g + +hT μ |
|
∂Ω |
; |
(3.25) |
||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
hu = r |
∂Ω, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ω – область задачи, а ∂Ω – граница области.
Рис. 3.78. Форма задания коэффициентов уравнения в коэффициентной форме в случае ОДУ одной переменной
Коэффициенты ea, da, c, α, γ, f, β, a, q, h, r определяются пользователем, при этом α, β, γ – векторные величины, а коэффициент с может быть матрицей в том случае, если среда анизотропна.
В общем случае u может быть вектором u = (u1;u2...un ). Тогда полученное уравнение приводится к системе скалярных уравнений,
акоэффициенты ea, da, c, α, γ, f, β, a, q, h будут матрицами NхN, а f
–вектором размерности N. hT – транспонированная матрица h. В
133

случае уравнения одной переменной, все коэффициенты задаются в одной вкладке (рис. 3.78).
Существуют два принципиально разных случая. Коэффициенты системы – константы, или зависят только от ко-
ординат и времени. В этом случае система ОДУ линейная. Коэффициенты системы зависят от переменной u или её произ-
водных. В этом случае система ОДУ будет нелинейная.
В случае системы ОДУ со многими переменными, каждый коэффициент задаётся на собственной вкладке (рис. 3.79).
Рис. 3.79. Форма задания коэффициентов уравнения в коэффициентной форме в случае ОДУ трёх переменных
Чтобы задать уравнение в коэффициентной форме, необходимо в навигаторе моделей выбрать пункт PDE Modes->PDE Coefficent form. Выберем нестационарный случай (Time-Dependent analisys).
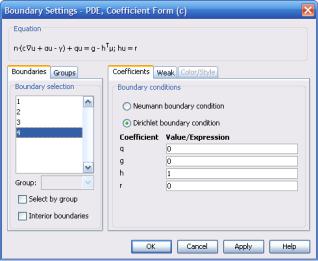
Второе и третье уравнения системы – граничные условия Неймана и Дирихле. Граничные условия Дирихле – это граничные условия первого рода, устанавливающие значение функции u на границе. Граничные условия Неймана – граничные условия второго рода, фиксирующие градиенты функции u. Форма постановки условий задана таким образом, что допустимо одновременное использование обоих условий (рис. 3.80). Это становится допусти-
134
мым за счёт наличия вектора с неопределёнными величинами μ, называемой множителем Лагранжа. Множитель (в случае системы ОДУ набор множителей) определяется в зависимости от остальных коэффициентов. Делается это следующим образом.
Рис. 3.80. Форма задания граничных условий для системы уравнений в коэффициентной форме
Укажем h=1. В этом случае, система граничных условий будет иметь вид:
n(c u + αu − γ)+ qu = g + μ;
u = r.
Второе уравнение – это граничное условие Дирихле, а первое приводится к нулю с помощью множителя μ.
Если указать h=0, r=0, то второе уравнение обращается 0=0, а первое будет иметь вид
n(c u +αu − γ)+ qu = g .
Это граничное условие Неймана.
Чтобы создать систему уравнений с несколькими переменными, следует в навигаторе моделей при задании прикладного режима в поле Dependent Variables указать через пробелы все переменные. Названия допускаются произвольные, однако рекомендуется ис-
135
пользовать общепринятые обозначения, например: u, v, w или u1,
u2, u3.
3.10.4. Генеральная форма
Генеральная форма уравнения предоставляет больше вольности в задании вида уравнения. Система уравнений выглядит следующим образом:
|
∂2u |
+ d |
∂u |
+ Γ = |
||||||
c |
a ∂t2 |
a ∂t |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂R |
μ |
|
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||
− nΓ = G + |
|
|
|
|
|
; |
||||
|
|
|||||||||
|
|
|
|
|
∂u |
|
|
∂Ω |
||
|
|
|
|
|
|
|
|
|
|
|
R = 0 |
∂Ω. |
|
|
|
|
|
|
|
||
F ;
Ω
(3.26)
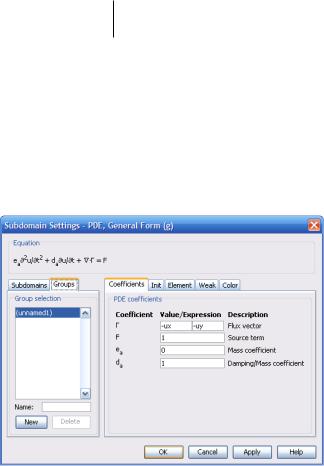
где коэффициенты ca, da, Γ, G задаются пользователем. Γ – векторная величина, а R – скалярная, под ними могут скрываться любые выражения, состоящие из производных разных порядков функции u по координатам и времени.
Рис. 3.81. Форма задания коэффициентов уравнения в генеральной форме
136
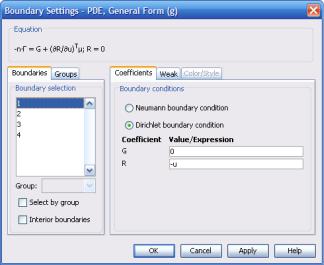
Если открыть режим уравнения в генеральной форме с помощью вызова пункта меню навигатора моделей PDE Modes->PDE Coefficent form->Time Dependent analisys и создать произвольную область, то по умолчанию в ней будет задано следующее уравнение (рис. 3.81) и граничные условия следующего вида (рис. 3.82).
Если подставить значения из полей в уравнение, показанное в поле Equation, получим следующую систему уравнений:
|
∂u |
− |
|
∂2u |
− |
∂2u |
=1 |
|
; |
|
|
||||||||||
|
∂t |
|
∂x |
2 |
∂y2 |
|
||||
|
|
|
|
|
|
Ω |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = 0 |
|
∂Ω. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
Граничные условия формируются по тому же принципу, что и в коэффициентной форме. Когда необходимо задать граничное условие Дирихле вида u=r, то следует указать поле R=u-r. В этом случае лагранжев множитель μ обращает в ноль условие Неймана. В случае выбора R=0 зануляется условие Дирихле.
Рис. 3.82. Форма задания граничных условий для уравнения в генеральной форме.
137

3.10.5.Слабая форма
Вслабой форме постановка задачи формулируется не системой уравнений, а интегральным равенством (1.3). Фактически это прямое явное использование метода конечных элементов в моделировании. В случае решения задач в коэффициентной и генеральной формах нет необходимости знать тонкости метода, программа все необходимые действия (умножение на тестовые функции, интегрирование, решение СЛАУ, подстановка коэффициентов) производит самостоятельно. При постановке задачи в слабой форме, существует возможность самостоятельно управлять процессом расстановки пробных функций, интегрированием и т.д.
Для того, чтобы выбрать режим уравнения в слабой форме следует выбрать пункт меню в навигаторе моделей PDE Modes- >Weak form, Subdomain (будем рассматривать стационарный случай). Нарисовав в данном режиме геометрическую область, можно посмотреть заданное по умолчанию в системе уравнение (рис. 3.83).
Рис. 3.82. Форма задания коэффициентов уравнения в слабой форме
В поле weak задаётся подынтегральное выражение (рис. 3.83). Фигурирующая в выражении функция test означает тестовую
138
функцию ϕi (x) . Напомним, что вид тестовой функции определяет-
ся во вкладке Element. Таким образом, полученное выражение представляет собой
∫(−ux ϕix −uy ϕiy +ϕi )dΩ=0 .
Что является слабой формой уравнения
∂2u + ∂2u = −1. ∂x2 ∂y2
3.11. Решение одномерных задач
Решение одномерных задач в FEMLAB – наименее ресурсоёмкий процесс. Большинство из них можно решить аналитически, или численно в пакетах Matlab или Maple, поэтому данная возможность не очень часто используется в FEMLAB. Тем не менее, система способна решать подобные уравнения намного быстрее, чем другие математические пакеты.
Решим следующую краевую задачу уравнения теплопроводности:
|
∂u |
− |
1 |
|
∂u |
= |
f ; |
|
|
∂t |
|
|
|
|
|||
a 2 |
|
∂x 2 |
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(3.27) |
u = u(x;t); x [0;l];t > 0; |
||||||||
u(0, t) = u0 ; |
|
|
|
|||||
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= β; |
|
|
|
|||
|
∂x |
x=l |
|
|
|
|||
|
|
|
|
|
|
|
|
|
u(x,0) = ϕ(x); |
|
|
||||||
Положим a=1, f=0, l=10; u0=0; β=π/5; φ(x)=sin(πx/5).
Чтобы выбрать размерность модели, равной 1, следует в выпадающем списке Space dimension выбрать пункт 1D. Список возможных прикладных режимов в данном случае будет намного меньше, чем для двумерных или трёхмерных моделей (рис. 3.84).
Выберем пункт PDE Modes->Classical PDEs->Heat Equation. На-
жав кнопку ОК, получим окно геометрии модели (рис. 3.85).
139

Рис. 3.84. Прикладные режимы одномерной геометрии в навигаторе моделей
Рис. 3.85. Рабочая область одномерной геометрии
140
