Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Красников Моделирование физических процессов с исползованием 2012

.pdf

Скачиваний:

172

Добавлен:

12.11.2022

Размер:

12.78 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

∂∂uxi = 0;i ∂σ

∂xik −ρgi = 0;k

εik = A(T )(σ')n−1 σ'ik .

А также граничные условия:

u = 0;v = 0;(x, y hb );

p = pàòì ;(x, y hs );

(3.15)

(3.16)

Можно выразить тензора напряжений и скоростей деформаций через их компоненты:

∂Fi

∂Fk

= σ

∂xk

∂xi

(3.17)

σik '=σik

−

pδik =

σik −

σllδik

(3.18)

•

∂ui

∂uk

εik

∂xk

∂xi

(3.19)

Здесь Fi , ui – соответствующие компоненты силы и скорости. В системе (3.15) берутся свёртки от тензоров:

σ =

;

ε ε 12

;

σ'=

σ'

12 .

ik ik

Обычно скорости течения льда находятся вдоль ледораздела – плоскости, на которой они максимальны. Поэтому наша задача принимает двумерный вид. Чтобы решить систему (3.15), необходимо её привести к наименьшему количеству переменных. В качестве таких переменных выбраны горизонтальная и вертикальная компоненты скорости u и v, и давление p. Для этого необходимо

101

выразить компоненты тензора напряжений через значения скоростей и давления через закон Глена:

σ'= B(T )ε	1n ;σ'	ik	= B(T )ε1−nn ε	.	(3.20)
		ik	ik

где B(T ) = (A(T ))−1n . В дальнейшем показатель Глена n принима-

ется равным 3. После указанных преобразований система (3.15) выглядит следующим образом:

∂u

∂v

∂x

∂y

∂

∂u

∂

μ ∂u

∂v

∂p

= 0,

∂x

∂y

∂x

∂y

∂x

(3.21)

∂

∂u

∂v

∂

∂v

∂p

−ρg

= 0,

∂x

∂y

∂x

∂y

2 −13

∂u

∂v 2

∂u

∂v

μ =

∂x

∂y

∂y ∂x

3.6.2. Постановка и решение задачи

Для решения задачи выберем стационарный режим уравнений Навье-Стокса. Обычно ледники распространяются на десятки километров, в то время как по вертикали разброс высот может быть на порядок меньше. В соответствии с этим промасштабируем ось X от 0 до 10000, а ось Y от 1 до 1000. На полученной области создадим тестовый ледник согласно рис. 3.42. Данная фигура создаётся прямой линией из координаты {(0,1000); (10000,200)}, а также кривой линией с теми же координатами и радиусом кривизны в точке (7000; 800). Не стоит обращать внимание на ломаное изображение полученной фигуры, это связано с недостаточно качественным автоматическим выбором сетки, впоследствии это будет исправлено.

102

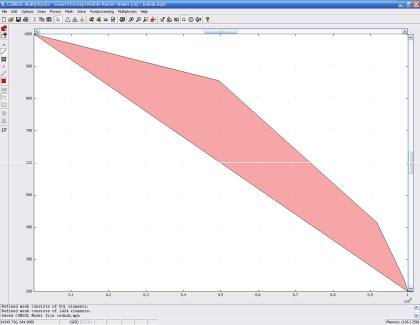
Рис. 3.42. Геометрия ледника

Следующий шаг – задание уравнения и граничных условий. Нужно привести уравнение к виду, представленному на форме Subdomain Settings. Плотность льда ρ = 900 кг/м3, вязкость льда

η = 0.5B(T ) ε−23 .

Из выражения (3.21) выделим компоненты силы:

∂

∂u

∂

∂u

∂v

∂x

∂y

∂x

(3.22)

∂y

∂

∂u

∂v

∂

∂v

− ρg.

∂y

∂x

∂y

Таким образом, форма будет иметь вид, соответствующий рис. 3.43.

103

Рис. 3.43. Задание коэффициентов системы уравнений

Все введённые выражения должны быть описаны в системе, иначе система не сможет их распознать. Для этого в окне констант Options->Constants (рис. 3.44) введём следующие величины:

patm	1E5	Атмосферное давление
g	9.81	Ускорение свободного падения
Tb	263	Температура ледника в К
A0	0.4499691550E-12	Постоянный коэффициент
Qakt	60E3	Энергия активации
R	8.3	Газовая постоянная

Рис. 3.44. Константы к задаче

104

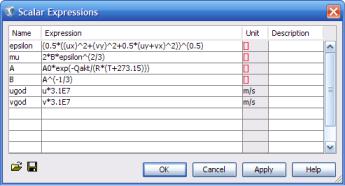
А в окне выражений Options->Expressions->Scalar Expressions

(рис. 3.45) укажем такие величины:

Epsilon	0.5((ux)^2+(vy)^2+0.5(uy+vx)^2))^(0.5)
mu	2Bepsilon^(2/3)
A	A0exp(-Qakt/(R(T+273.15)))
B	A^(-1/3)
ugod	u*3.1E7
vgod	v*3.1E7

Рис. 3.45. Скалярные выражения к задаче

Задание граничных условий выглядит следующим образом. На нижней границе выставляется условие прилипания (No slip) или Inflow/outflow velocity с указанием обеих компонент скорости, равными нулю. На верхней свободной границе необходимо указать давление равное атмосферному. Для этого выбирается тип условий Outflow/Pressure, который позволяет задавать условия в виде давления (рис. 3.46).

105

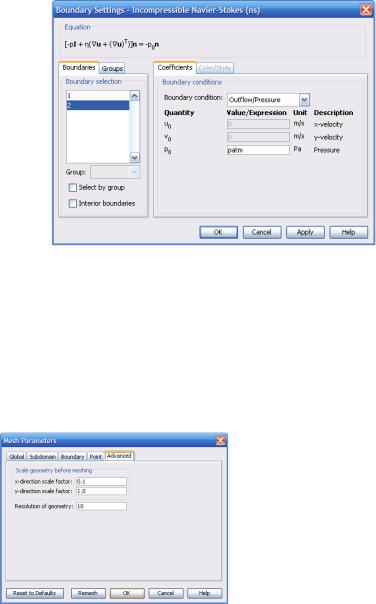
Рис. 3.46. Задание граничного условия на верхней границе

Далее нужно задать правильную разбивку по сетке. Поскольку наша область вытянута по оси х, то конечные элементы должны быть также вытянуты по этой оси. Для этого в окне Mesh parameters во вкладке Advanced укажем значение поля х-direction scale factor, равным 0,1 (рис. 3.47).

Полученная сетка будет равномерной относительно нашей системы координат (рис. 3.48). Запустив решение, получим следующее распределение скоростей течения льда (рис. 3.49). Скорости в леднике имеют небольшие значения, порядка метров в год. Чтобы изменить размерность величины, выберем пункт меню

Postprocessing->Plot Parameters, где во вкладке Surface

в поле Expression укажем переменную ugod, определённую в константах. Данная переменная переводит размерность горизонтальной скорости течения в м/год.

Рис. 3.47. Масштабирование сетки.

106

Рис. 3.48. Масштабированная сетка на растянутой области

Указав в качестве выражения для графика ux, получим распределение производной скорости течения по оси Х (рис. 3.50).

Рис. 3.49. Распределение горизонтальной скорости течения льда в леднике

107

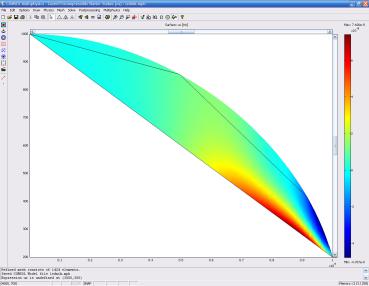
Рис. 3.50. Распределение производной горизонтальной скорости по оси Х

3.7. Реализация мультифизического режима

Одно из мощных преимуществ, предлагаемое системой FEMLAB в версии 3.2 – это возможность совмещать решение двух и более задач. Чтобы его рассмотреть, усложним немного предыдущую задачу.

Константа А, входящая в выражение (3.14), зависит от температуры

			Q
A(T ) = A	exp	−	akt	.	(3.23)

0			RT

Впредыдущей задаче температура имеет постоянное значение

–10° С. Рассчитаем температуру в леднике, решив уравнение теплопроводности в течение одного года

108

	∂T		1
	∂T	−	1	T = 0;
	∂t	−	a	T = 0;
	∂t		a					(3.24)
		∂T


−k				= QGEO ;
−k		∂x		= QGEO ;
				x=Hb
				x=Hb
					2πt
					2πt
T (x = xs ) =Ts + AT sin(								),
T (x = xs ) =Ts + AT sin(						t		),
						t	g
							g
где,	a =1,18*10−6 м2/с –						коэффициент температуропроводности

льда, k=2.23 Вт/м – коэффициент теплопроводности льда. На нижней границе выполняется граничное условие второго рода – поток равен геотермическому: QGEO=0.042 Вт/м2.

Температура на поверхности льда будет равна температуре атмосферы, которая меняется в течение года по синусоидальному закону. Положим среднюю температуру Ts=-10ºC, а амплитуду колебаний в течение года AT=5º.

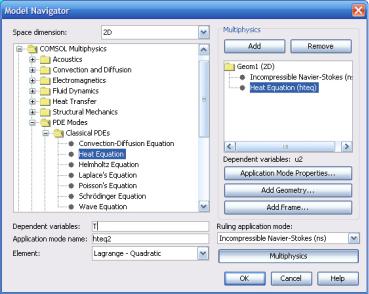
Для реализации мультифизического режима вызовем навига-

тор моделей пунктом меню Multiphysics->Model Navigator

(рис. 3.51).

Рис. 3.51. Загрузка мультифизического режима в навигаторе моделей

109

В окне навигатора моделей выберем пункт PDE Models- >Classical PDEs->Heat Equation. В Dependent variables необхо-

димо указать название переменной данного прикладного режима. По умолчанию она называется u2, во избежание путаницы сменим её название на T (температура).

После выбора режима нажмём кнопку Add. Так уравнение теплопроводности появляется в списке режимов нашей задачи. Для продолжения работы необходимо нажать OK. Теперь режим уравнения теплопроводности является активным режимом в нашей задаче. Чтобы переключиться обратно на режим уравнений гидродинамики, можно выбрать его в списке имеющихся режимов в разде-

ле меню Multiphysics.

В окне Subdomain Settings в поле da укажем коэффициент температуропроводности 1.18*10-6. Так как в нашей задаче нет источника, то в поле f укажем 0. Поле с оставим без изменений. В качестве граничных условий для нижней границы укажем граничные условия второго рода (Неймана) согласно выражению (3.24). Для верхней будут выполняться периодические граничные условия

(рис. 3.53, 3.54).

Рис. 3.52. Задание коэффициентов уравнения теплопроводности

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20224.08 Mб43Королев Датчики и детекторы физико-енергетических установок 2011.pdf
#
12.11.20221.43 Mб2Королев Лабораторая работа применение современных опен-соурце.pdf
#
12.11.2022816.16 Кб15Коротеев Лабораторный практикум по курсу Електротехника 2011.pdf
#
12.11.20221.63 Mб65Короткова Задачник по курсу Математическая лингвистика и 2012.pdf
#
12.11.20229.22 Mб121Красавин Компютерныы практикум в среде МатЛаб 2015.pdf
#
12.11.202212.78 Mб172Красников Моделирование физических процессов с исползованием 2012.pdf
#
12.11.20222.58 Mб6Критсына Лабораторныы практикум по курсу Статистические методы 2015.pdf
#
12.11.20222.51 Mб19Круглов Руководство по технической термодинамике 2012.pdf
#
12.11.20225.91 Mб23Крушный Синтез цифровых управляюсчих автоматов 2011.pdf
#
12.11.20223.84 Mб1Крючков Фундаменталс оф Нуцлеар Материалс Пхысицал Протецтион 2011.pdf
#
12.11.20222.1 Mб0Кувяткина Бухгалтерский учет и аудит внешнеекономической 2012.pdf