13.2. Средняя квадратическая, предельная и относительная ошибки

Для суждения о степени точности ряда измерений нужно иметь среднее значение ошибки. Среднее арифметическое из измерений нельзя брать, так как из-за разных знаков ряд с отдельными крупными ошибками может оказаться точнее ряда с меньшими ошибками:

25,5; 24,5; 25,0 – m_ср.=0 Х=25 м.

25,04; 24,97; 25,04 – m_ср.=0,02 м

Если взять ошибки по абсолютной величине, то два ряда измерений с одинаковыми по абсолютной величине средними ошибками могут быть ошибочно приняты равноточными и наличие крупных ошибок не будет отражено:

Поэтому в качестве критерия для оценки точности ряда измерений используют не зависящую от знаков отдельных ошибок и рельефно показывающую наличие крупных ошибок среднюю квадратическую ошибку. Квадрат этой ошибки принимают равным среднему арифметическому из квадратов отдельных случайных ошибок, то есть:

– формула Гаусса, где Δ – истинная ошибка измерения.

По теории вероятностей подсчитано, что при большом количестве измерений случайная ошибка одного измерения превосходит m.

∆>1m – в 32 случаях из 100 измерений.

∆>2m – в 5 случаях из 100 измерений.

∆>3m – в 3 случаях из 1 000 измерений.

Поэтому утроенную среднюю квадратическую ошибку считают предельной ∆_lim=3m.

Часто точность произведенных измерений лучше оценивается относительной ошибкой, то есть отношением абсолютной ошибки к измеряемой величине, выражаемой правильной дробью с числителем, равным 1. Эта ошибка характеризует в основном линейные измерения и измерения площади участков. Например, в замкнутом полигоне теодолитного хода линейные измерения оцениваются относительной ошибкой 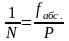; где – абсолютная ошибка, Р – периметр полигона.

13.3. Средняя квадратическая ошибка функции измеренных величин

а) Функция общего вида:

.

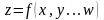Пусть аргументы измерены с ошибками ∆x₁, ∆x₂,…; ∆y₁, ∆y₂,…; ∆w₁, ∆w₂…

Тогда

.

Так как ошибки ∆x, ∆y, ∆w малы, то функцию можно разложить в ряд Тейлора, ограничившись членами первой степени:

Отсюда составим систему уравнений случайных ошибок:

.

Но ∆x, ∆y…имеют бесконечное число измерений каждая и характеризуются средними квадратическими ошибками. Поэтому можно составить бесконечное число уравнений, аналогичных выше приведенному:

Возведем равенства в квадрат, сложим и разделим на n.

0 n→∞.

Отсюда

→ .

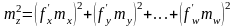Квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на средние квадратические ошибки соответствующих аргументов.

б) Функция вида z=x+y (суммы), m_z=?

Дано: х – измерено несколько раз с ошибками ∆х₁; ∆х₂,… ∆х_n

у – измерено несколько раз с ошибками ∆у₁, ∆у₂,… ∆у_n

z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,… ∆z_n.

;

.

Эта же формула справедлива для функции вида z=x–y, так как после выше приведенных рассуждений перед последним членом будет знак (–). Но он все равно стремится к нулю.

Поэтому можно сделать вывод, что квадрат средней квадратической ошибки алгебраической суммы двух аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Если m_х=m_у=m, то m_z=± .

Пусть , перепишем . Тогда можно записать:

, но , поэтому

.

Если 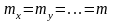, то при n слагаемых , то есть квадрат средней квадратической ошибки суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Средняя квадратическая ошибка алгебраической суммы измеренных с одинаковой точностью величин в раз больше средней квадратической ошибки одного слагаемого.

в) Функция вида 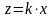(произведения).

k – постоянное число безошибочное.

х – измерено несколько раз с ошибками ∆х₁, ∆х₂,… ∆х_n.

z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,…, ∆z_n.

отсюда или ,

то есть средняя квадратическая ошибка произведения постоянного числа на аргумент равна произведению постоянного числа на среднюю квадратическую ошибку аргумента (измеряемой величины).