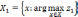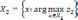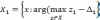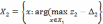- •Условные сокращения
- •Введение
- •1. Менеджмент риска информационной безопасности
- •1.1. Основные термины и определения
- •1.2. Система менеджмента информационной безопасности
- •1.3. Менеджмент риска информационной безопасности
- •Конец первой и последующих итераций
- •1.3.1. Установление контекста
- •1.3.2. Оценка риска нарушения информационной безопасности
- •1.3.2.1. Анализ риска
- •1.3.2.1.1. Идентификация риска
- •1. Определение (идентификация) активов
- •Реестр информационных ресурсов Компании
- •2. Определение угроз
- •Определение существующих мер и средств контроля и управления
- •Выявление уязвимостей
- •5. Определение последствий
- •1.3.2.1.2. Установление значения риска (количественная оценка риска)
- •1.3.2.2. Оценивание риска
- •1.3.3. Обработка риска
- •1) Снижение риска
- •2) Сохранение риска
- •Предотвращение риска
- •Перенос риска
- •1.3.4. Принятие риска
- •1.3.5. Коммуникация риска
- •1.3.6. Мониторинг и переоценка риска
- •1.4. Стандарты в области управления информационными рисками
- •1.5. Инструментальные средства для управления рисками
- •1.5.9. Гриф 2006
- •1.5.10. АванГард
- •1.6. Контрольные вопросы
- •2. Математические основы принятия решений при управлении рисками
- •2.1. Основные понятия и обобщенная классификация задач принятия решений
- •2.2. Формальное описание моделей принятия решений
- •2.3. Методы экспертных оценок
- •2.3.1. Методологические основы и предпосылки применения методов экспертных оценок
- •2.3.2. Основные типы шкал
- •2.3.3. Методы проведение экспертизы
- •2.3.4. Качественные экспертные оценки
- •2.3.5. Этапы работ по организации экспертной оценки
- •2.3.6. Отбор экспертов и их характеристика
- •2.3.7. Методы опроса экспертов
- •2.3.8. Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
- •2.4. Детерминированные модели и методы принятия решений
- •2.4.1. Постановка многокритериальных задач принятия решений
- •2.4.2. Характеристики приоритета критериев. Нормализация критериев
- •2.4.3. Принципы оптимальности в задачах принятия решений
- •2.4.4. Постановка задач оптимизации на основе комбинирования принципов оптимальности
- •2.4.5. Теория полезности. Аксиоматические методы многокритериальной оценки
- •2.4.6. Метод аналитической иерархии
- •2.4.7. Методы порогов несравнимости электра
- •2.5. Статистические модели и методы принятия решений в условиях неопределенности
- •2.5.1. Статистическая модель однокритериального принятия решений в условиях неопределенности
- •2.5.2. Построение критериев оценки и выбора решений для первой ситуации априорной информированности лпр
- •2.5.2.1. Критерий Байеса-Лапласа
- •2.5.2.2. Критерий минимума среднего квадратического отклонения функции полезности или функции потерь
- •2.5.2.3. Критерий максимизации вероятности распределения функции полезности
- •2.5.2.4. Модальный критерий
- •2.5.2.5. Критерий минимума энтропии математического ожидания функции полезности
- •2.5.2.6. Критерий Гермейера
- •2.5.2.7. Комбинированный критерий. Объединение критериев Байеса-Лапласа и среднего квадратического отклонения функции полезности (потерь)
- •2.5.3. Построение критериев оценки и выбора решений для второй ситуации априорной информированности лпр
- •2.5.3.1. Максиминный критерий Вальда
- •2.5.3.2. Критерии минимаксного риска Сэвиджа
- •2.5.4. Построение критериев оценки и выбора решений для третьей ситуации априорной информированности лпр
- •2.5.4.1. Критерий Гурвица
- •2.5.4.2. Критерий Ходжеса-Лемана
- •2.5.5. Пример оценки отдельных характеристик качества информационной системы в условиях неопределенности
- •2.5.6. Статистическая модель многокритериального принятия решений на основе принципов оптимальности в условиях неопределенности
- •2.5. Методы оптимизации
- •2.7. Контрольные вопросы
- •Заключение
- •Приложение Справочные данные
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
2.4.3. Принципы оптимальности в задачах принятия решений
Рассмотрим подход к проблеме многокритериальности, основанный на введении понятия лучших решений и опирающийся на постулируемые принципы оптимальности. Принципы оптимальности можно трактовать как обобщенные критерии качества (критерии оптимальности), являющиеся математическим выражением цели принятия решений, которое позволяет оценить степень достижения этой цели. Выбор принципа или его конструкции остается за ЛПР [68].
Принцип
оптимальности по Парето. Данный
принцип может быть использован на
начальной стадии решения задачи в целях
уменьшения исходного множества решений
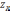 .
.
Решение (альтернативу) называют оптимальным по Парето (парето-оп- тимальным, паретовским, эффективным), если невозможно улучшить (увеличить) решение ни по одному из критериев без ухудшения (уменьшения) решения хотя бы по одному из критериев. Парето-оптимальные решения (альтернативы) составляют множество Парето (множество эффективных решений, множество -оптимальных альтернатив, множество компромиссов).
Пусть 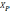 является множеством Парето в пространстве
независимых переменных (параметров) и
является множеством Парето в пространстве
независимых переменных (параметров) и
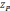 — множество Парето в пространстве
критериев. Тогда эти множества могут
быть описаны следующими моделями:
— множество Парето в пространстве
критериев. Тогда эти множества могут
быть описаны следующими моделями:
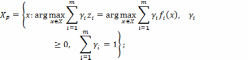
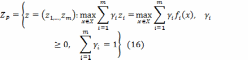
Данное описание корректно для выпуклого множества . На рис. 2.3 приведены примеры выпуклых паретовских множеств для непрерывного и дискретного случаев.
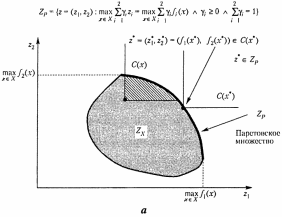
Рис. 2.3. Примеры выпуклых непрерывного (а) и дискретного (б)
множеств Парето
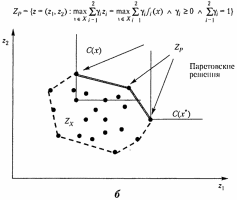
Рис. 2.3. Примеры выпуклых непрерывного (а) и дискретного (б)
множеств Парето (продолжение)
Введем еще одно
понятие. Альтернатива
доминирует по Парето альтернативу
( альтернатива
лучше по Парето альтернативы
),
если
альтернатива
лучше по Парето альтернативы
),
если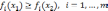 ,
и хотя бы для одного i такое неравенство
является строгим. Те альтернативы, для
которых не существует доминирующих их
допустимых альтернатив
,
называются оптимальными по Парето.
,
и хотя бы для одного i такое неравенство
является строгим. Те альтернативы, для
которых не существует доминирующих их
допустимых альтернатив
,
называются оптимальными по Парето.
Множество альтернатив
(векторных оценок) в пространстве
критериев, доминирующих по Парето
альтернативу х (векторную оценку
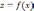 ,
совпадает с положительным ортантом
(конусом) С(х), вершина которого
перенесена в точку f(x). Для любой
точки (альтернативы)
,
совпадает с положительным ортантом
(конусом) С(х), вершина которого
перенесена в точку f(x). Для любой
точки (альтернативы) 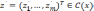 выполняются неравенства
выполняются неравенства 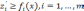 .
Если
.
Если 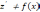 ,
то хотя бы одно из неравенств будет
строгим. Если пересечение положительного
ортанта
,
то хотя бы одно из неравенств будет
строгим. Если пересечение положительного
ортанта 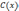 с множеством векторных оценок
содержит какие-либо точки кроме
с множеством векторных оценок
содержит какие-либо точки кроме 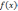 ,
то каждая из этих точек доминирует х
по Парето. Альтернатива х*
π-оптимальна, если пересечение конуса
,
то каждая из этих точек доминирует х
по Парето. Альтернатива х*
π-оптимальна, если пересечение конуса
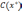 с множеством векторных оценок
состоит из единственной точки
с множеством векторных оценок
состоит из единственной точки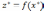 .
.
Применение описанной методики позволяет легко проверять π-оптимальность альтернативы.
Структура моделей
(15) приводит к простому алгоритму
построения множества Парето: определить
множество Г величин весового вектора
,
найти паретовские точки по выражению
(15) для каждого  ,
построить конечно-разностную аппроксимацию
пареговского множества по полученным
точкам.
,
построить конечно-разностную аппроксимацию
пареговского множества по полученным
точкам.
Рассмотрим более
общий случай, когда множество
невыпукло. Предположим, что множество
векторных оценок
ограничено, замкнуто и целиком лежит
во внутренности неотрицательного
ортанга пространства критериев  .
Это означает, что
.
Это означает, что  .
Ограниченность и замкнутость множества
гарантирует существование π-оптимальных
альтернатив. Условие того, что
целиком лежит во внутренности
неотрицательного ортанта пространства
критериев, введено для удобства. Любое
ограниченное множество в
можно сдвинуть в положительный ортант,
например, используя сравнительную
нормализацию, и отношение доминирования
по Парето между точками не изменится.
.
Ограниченность и замкнутость множества
гарантирует существование π-оптимальных
альтернатив. Условие того, что
целиком лежит во внутренности
неотрицательного ортанта пространства
критериев, введено для удобства. Любое
ограниченное множество в
можно сдвинуть в положительный ортант,
например, используя сравнительную
нормализацию, и отношение доминирования
по Парето между точками не изменится.
Пусть в точке 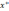 векторная оценка
векторная оценка 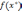 π-оптимальна, т.е. пересечение конуса
с множеством векторных оценок
состоит только из этой точки. При
невыпуклом множестве
может не существовать функция вида
π-оптимальна, т.е. пересечение конуса
с множеством векторных оценок
состоит только из этой точки. При
невыпуклом множестве
может не существовать функция вида
 ,
которая достигла максимального значения
в точке
,
которая достигла максимального значения
в точке  .
.
Так как пересечение
конуса
с множеством
состоит из единственной точки, то можно
считать, что граница этого конуса
является множеством (поверхностью)
уровня некоторой функции 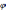 ,
где
,
где 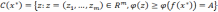 ,
которая достигает максимума на множестве
в точке
.
Проведем через начало координат и точку
,
которая достигает максимума на множестве
в точке
.
Проведем через начало координат и точку
 прямую линию, которая описывается
уравнениями
прямую линию, которая описывается
уравнениями

В точке
выполняются условия 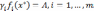 .
.
В двумерном случае
при 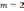 легко заметить, что линиями уровня
функции
,
проходящими через точку
легко заметить, что линиями уровня
функции
,
проходящими через точку 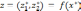 ,
являются лучи, идущие из точки
,
являются лучи, идущие из точки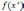 и удовлетворяющие условиям:
и удовлетворяющие условиям:
для луча под прямой
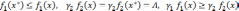
для луча над прямой
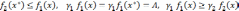
Отсюда можно сделать вывод, что функция представима в виде
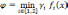
При обобщении на
m-мерный случай
справедливо следующее. Пусть множество
π-оптимальных векторных оценок
ограничено, замкнуто и целиком лежит
во внутренности неотрицательного
ортанта
.
Чтобы альтернатива х* была π-оптимальна,
необходимо и достаточно, чтобы существовали
коэффициенты 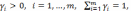 удовлетворяющие
условию
удовлетворяющие
условию
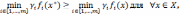
причем равенство имеет место тогда и только тогда, когда
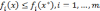 .
.
Теперь множество Парето для невыпуклого случая в пространстве критериев можно описать следующими моделями:
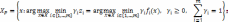
(16)
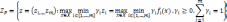
Данный результат
полезен для того, чтобы показать, что
альтернатива х* π-оптимальна, или
найти 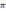 -оптимальную
альтернативу, доминирующую х*. На
рис. 2.4 приведены примеры невыпуклых
паретовских множеств для дискретного
и непрерывного случаев.
-оптимальную
альтернативу, доминирующую х*. На
рис. 2.4 приведены примеры невыпуклых
паретовских множеств для дискретного
и непрерывного случаев.

Рис. 2.4. Примеры невыпуклых дискретного (a) и непрерывного (б) множеств Парето

Рис. 2.4. Примеры невыпуклых дискретного (a) и непрерывного (б)
множеств Парето (продолжение)
Отметим, что в общем случае приходится решать негладкую задачу максимизации (16), ее решение может быть не единственным и не все решения будут -оптимальными. Для устранения неоптимальных альтернатив необходимо все решения проверять на доминируемость по Парето.
Сформулируем алгоритм построения множества Парето для невыпуклого случая: определить множество (набор значений) величин весового вектора , найти паретовские точки по моделям (16) для каждого , проверить эти точки на доминируемость по Парето; исключить точки, неоптимальные по Парето; построить конечно-разностную аппроксимацию па- ретовского множества по полученным точкам.
Одним из преимуществ паретовского принципа оптимальности является его инвариантность к масштабу, единицам измерения критериев и взаимной важности критериев. Недостаток принципа заключается в отсутствии ответа на вопрос: какое из решений лучшее?
Следующие принципы дают ответ на этот вопрос. При изложении принципов оптимальности будем предполагать, что множество векторных оценок ограниченно, замкнуто и целиком лежит во внутренности неотрицательного ортанта пространства критериев .
Принцип идеальной
точки. Согласно принципу идеальной
точки лучшим считается решение,
расположенное в пространстве параметров
ближе всего (в смысле некоторой нормы)
к «идеальной точке» 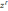 :
:
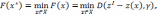
где
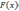 — целевая функция или функция качества;
— целевая функция или функция качества;
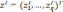 — идеальная точка;
— идеальная точка; 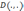 — норма;
— весовой вектор.
— норма;
— весовой вектор.
Запись, приведенная выше, часто называется сверткой значений критериев или просто сверткой.
В случае применения евклидовой нормы получим
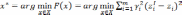 .
.
Для удобства можно использовать относительные величины:
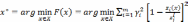 .
.
В более общем случае для нормы Гельдера имеем
 .
.
Идеальная точка может быть выбрана ЛПР интуитивно или взята формально как вектор максимальных значений каждого из критериев в отдельности:

Этот принцип выражает желание найти решение, ближайшее к идеальной точке. Изменяя норму и весовой вектор у, можно получить разные свертки (целевые функции), которые по-разному описывают понятие «близости» к идеальной точке.
На рис. 2.5 приведена графическая иллюстрация принципа идеальной точки в случае невыпуклого множества для дискретного и непрерывного случаев.
.
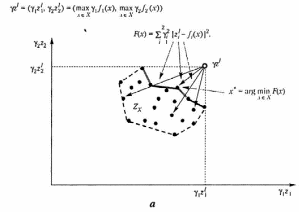
Рис. 2.5. Примеры применения принципа идеальной точки для невыпуклых
дискретного (а) и непрерывного (б) множеств
Рис.2.5. Примеры применения принципа идеальной точки для невыпуклых
дискретного (а) и непрерывного (б) множеств (продолжение)
Принцип
антиидеальной точки. В
соответствии с этим принципом лучшим
считается наиболее удаленное решение
от антиидеальной точки 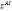 :
:
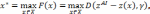
где
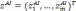 — антиидеальная точка, которая может
быть выбрана следующим образом:
— антиидеальная точка, которая может
быть выбрана следующим образом:
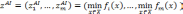
Для евклидовой нормы и нормы Гельдера принцип имеет вид
 ,
,
 ,
,
или для относительных величин
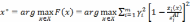 ;
;
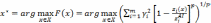 .
.
Данный принцип выражает желание найти решение, наиболее удаленное от антиидеалыюй точки.
На рис. 2.6 дана графическая иллюстрация принципа антиидеальной точки для невыпуклых дискретного и непрерывного множеств .
Следующие пять принципов выражают желание равномерно увеличивать величины всех локальных критериев при определении наилучшего решения.
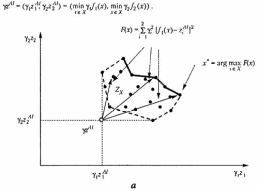
Рис. 2.6. Примеры применения принципа антиидеальной точки для невыпуклых дискретного (а) и непрерывного (б) множеств
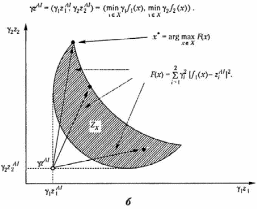
Рис. 2.7. Примеры применения принципа антиидеальной точки для невыпуклых дискретного (а) и непрерывного (б) множеств (продолжение)
Принцип равенства. Согласно этому принципу наилучшим будет следующее решение:
 ,
,
где
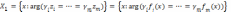
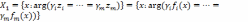
Здесь решение ищется на прямой в пространстве критериев. Возможны случаи, когда найденное решение не будет паретовским.
На рис. 2.7 и 2.8 приведена графическая иллюстрация применения принципа равенства для случаев невыпуклых дискретного и непрерывных множеств .

Рис. 2.8. Примеры удачного применения принципа равенства для невыпуклых дискретного (а) и непрерывного (б) множеств
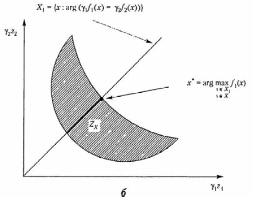
Рис. 2.9. Примеры удачного применения принципа равенства для невыпуклых дискретного (а) и непрерывного (б) множеств (продолжение)
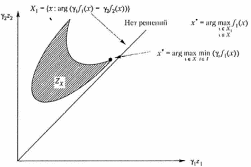
Рис. 2.10. Пример неудачного применения принципа равенства для невыпуклого непрерывного множества
Принцип квазиравенства. Это смягченная версия слишком «жесткого» принципа равенства. По данному принципу наилучшее решение определяется как точка:

где
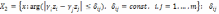
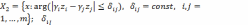 – заранее выбранная константа или
величина, изменяемая ЛПР, которая
позволяет значениям критериев отклоняться
друг от друга.
– заранее выбранная константа или
величина, изменяемая ЛПР, которая
позволяет значениям критериев отклоняться
друг от друга.
На рис. 2.9 и 2.10 приведена графическая иллюстрация принципа квазиравенства для случаев невыпуклых дискретного и непрерывных множеств .
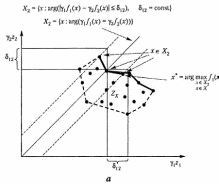
Рис. 2.11. Примеры применения принципа квазиравенства для невыпуклых дискретного (а) и непрерывного (б) множеств
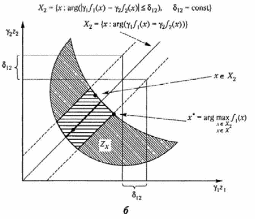
Рис. 2.12. Примеры применения принципа квазиравенства для невыпуклых дискретного (а) и непрерывного (б) множеств (продолжение)
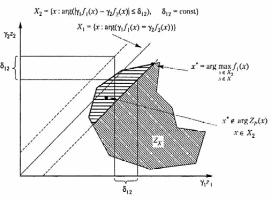
Рис. 2.13. Пример неудачного применения принципа квазиравенства для невыпуклого непрерывного множества
Принцип максимина. По данному принципу каждое решение описывается наименьшей взвешенной величиной из m критериев. Затем выбирается наибольшее среди этих наименьших значений и соответствующее ему решение принимается за наилучшее:
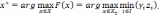
где
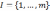 — множество номеров критериев, ряд
приоритета.
— множество номеров критериев, ряд
приоритета.
Иногда данный принцип называют принципом гарантированного результата или принципом наибольшей осторожности. Для графической иллюстрации можно рассмотреть рис. 2.6. Максимннное решение в этих примерах совпадает с решением, полученным с помощью принципа равенства. На рис. 2.7 указано найденное максиминное решение при отсутствии решения по принципу равенства.
Принцип последовательного максимина. Если принцип максимина не приводит к единственному решению, то он может быть последовательно применен до m раз:
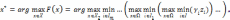
где
 – множество номеров критериев, полученное
из множества I,
из которого исключена единица (номер
критерия с минимальным значением);
– множество номеров критериев, полученное
из множества I,
из которого исключена единица (номер
критерия с минимальным значением);
 — множество номеров критериев, полученное
из множества
,
из которого исключена двойка; ...;
— множество номеров критериев, полученное
из множества
,
из которого исключена двойка; ...;  — множество, которое содержит только
число m
(состоит из номера одного критерия).
— множество, которое содержит только
число m
(состоит из номера одного критерия).
Квазиоптимальный
принцип последовательного максимина.
Это смягченная версия принципа
последовательного максимина. Принцип
последовательного максимина может быть
последовательно применен до m
раз. Каждое максиминное i-e
решение ослабляется на величину  такое ослабление производят до m
раз. По данному
принципу наилучшее решение ищется как
точка:
такое ослабление производят до m
раз. По данному
принципу наилучшее решение ищется как
точка:
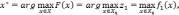
где
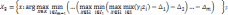
 – заранее выбранные
константа или величины (изменяемые
ЛПР), которые позволяют расширить
множество допустимых значений. Критерий
для максимизации может быть выбран ЛПР.
– заранее выбранные
константа или величины (изменяемые
ЛПР), которые позволяют расширить
множество допустимых значений. Критерий
для максимизации может быть выбран ЛПР.
Стремление увеличивать значения всех критериев одновременно является привлекательным. Однако отклонение от приведенных принципов иногда может дать значительный выигрыш, например, если позволить ухудшать значения части критериев для достижения улучшения значений по другим критериям.
Следующие два принципа носят название принципов справедливой уступки. Понятие «справедливости» может быть описано разными способами. До сих пор не установлено простого и очевидного «справедливого» принципа. Он и не может существовать, поскольку различные ситуации требуют разной «справедливости». Компромисс и справедливость всегда привязаны к конкретной ситуации или к классу ситуаций. Рассмотрим подход к «справедливости», основанный на сравнении оценок увеличения и уменьшения значений локальных критериев при сравнении различных решений. Данный подход приводит к двум принципам: абсолютной и относительной уступки.
Принцип абсолютной уступки. Пусть сравниваются два любых решения и осуществляется переход от первого ко второму решению. Пусть при этом переходе величины одной части критериев уменьшаются, а второй — увеличиваются. Согласно рассматриваемому принципу второе решение лучше первого, если сумма взвешенных значений увеличившихся критериев больше суммы взвешенных значений уменьшившихся критериев. Это определение и принцип абсолютной уступки могут быть выражены в простой математической форме:
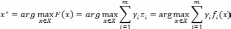
Описанный принцип позволяет улучшать качество решения за счет компенсации (уступки) уменьшения значений по одним критериям большим увеличением значений по другим критериям. Приведенная свертка в виде взвешенной суммы величин критериев может рассматриваться как целевая функция или функция качества.
На рис. 2.11 и 2.12 дана графическая иллюстрация принципа абсолютной уступки для случаев невыпуклых и выпуклого дискретного и непрерывных множеств .
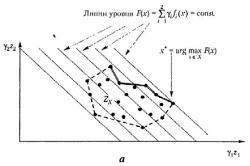
Рис. 2.14. Примеры применения принципа абсолютной уступки для невыпуклых дискретного (а) и непрерывного (б) множеств

Рис. 2.15. Примеры применения принципа абсолютной уступки для невыпуклых дискретного (а) и непрерывного (б) множеств (продолжение)
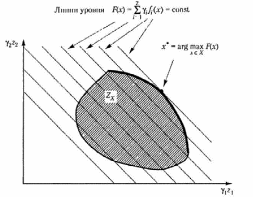
Рис. 2.16. Пример применения принципа абсолютной уступки для выпуклого непрерывного множества
Принцип относительной уступки. Пусть сравниваются два любых решения и осуществляется переход от первого ко второму решению. При этом переходе относительные величины одной части критериев уменьшаются, а относительные величины второй части критериев увеличиваются. Согласно принципу относительной уступки второе решение лучше первого, если суммарное относительное увеличение взвешенных значений увеличившихся критериев больше суммарного относительного уменьшения взвешенных значений уменьшившихся критериев. Принцип относительной уступки и данное определение могут быть выражены в простой математической форме:
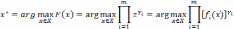
или
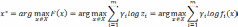
Этот принцип учитывает значения критериев, и самый простой путь улучшения решения заключается в уменьшении значений критериев с большими значениями.
На рис. 2.13 приведена графическая иллюстрация принципа относительной уступки для случаев невыпуклого дискретного и выпуклого непрерывного множеств .
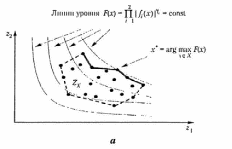
Рис. 2.17. Примеры применения принципа относительной уступки для невыпуклого дискретного (а) и выпуклого непрерывного (6) множеств , а также выпуклого непрерывного множества и логарифмических шкал (в)
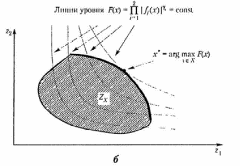
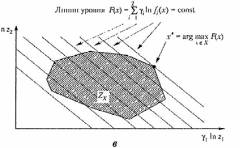
Рис. 2.18. Примеры применения принципа относительной уступки для невыпуклого дискретного (а) и выпуклого непрерывного (6) множеств , а также выпуклого непрерывного множества и логарифмических шкал (в) (продолжение)
Принцип абсолютной уступки не учитывает значений локальных критериев. Его лучше использовать в комбинации с другими принципами. Принцип относительной уступки довольно чувствителен к величинам критериев, и относительная уступка ведет к учету интересов, прежде всего, критериев с наибольшими значениями за счет критериев с меньшими значениями. Важным преимуществом принципа относительной уступки является его инвариантность к единицам, в которых измеряются значения критериев.
Все описанные принципы оптимальности используют весовой вектор. Приводимые далее принцип главного критерия и лексикографический принцип основаны на меньшем объеме информации о взаимной важности критериев.
Принцип главного критерия. Это наиболее широко используемый принцип при постановке задач оптимизации. Один из критериев (обычно самый важный) принимается за главный, для остальных критериев назначают пороговые величины. Величины этих критериев должны превышать пороговые значения. Наилучшим решением является точка:


Выбор
пороговых значений  очень важен. Изменяя их, можно получать
различные решения. Кроме того, можно
рекомендовать при применении данного
принципа исследовать, как влияет выбор
главного критерия на результирующее
оптимальное решение.
очень важен. Изменяя их, можно получать
различные решения. Кроме того, можно
рекомендовать при применении данного
принципа исследовать, как влияет выбор
главного критерия на результирующее
оптимальное решение.
На рис. 2.14 дана графическая иллюстрация принципа главного критерия для случаев невыпуклых дискретного и непрерывного множеств .
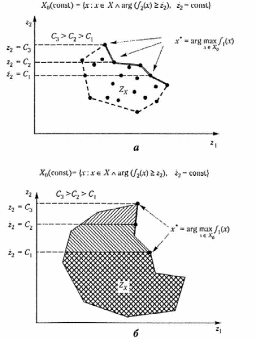
Рис. 2.19. Примеры применения принципа главного критерия для невыпуклых дискретного (а) и непрерывного (б) множеств
Лексикографический принцип. В этом случае используется ряд приоритета и решается последовательность задач. Сначала максимизируется самый важный критерий. Полученное в результате множество решений является допустимым множеством для максимизации следующего по важности критерия и т.д.:
m.
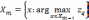
Данный принцип является довольно жестким. Часто после решения первой задачи максимизации получают единственное решение, а остальные критерии не участвуют в решении, и тем самым их «интересы» не учитываются. На рис. 2.15 приведена графическая иллюстрация лексикографического принципа для случаев невыпуклого дискретного и выпуклого непрерывного множеств .
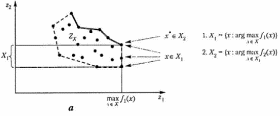
Рис. 2.20. Примеры применения лексикографического принципа оптимальности для невыпуклого дискретного (а) и выпуклого непрерывного (б) множеств
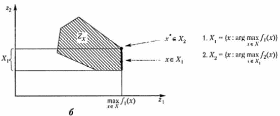
Рис. 2.21. Примеры применения лексикографического принципа оптимальности для невыпуклого дискретного (а) и выпуклого непрерывного (б) множеств (продолжение)
Следующий принцип более гибкий.
Лексикографический принцип квазиоптимальности. Решается последовательность задач максимизации с введенными отклонениями от оптимума (уступками). Данные отклонения увеличивают допустимое множество, на котором решаются последующие задачи минимизации:
m-1.
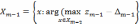
m.
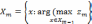
Принцип
позволяет ЛПР выбирать величины 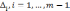 ,
и влиять
,
и влиять
на решение и «интересы» последующих критериев.
На рис. 2.16 дана графическая иллюстрация лексикографического принципа квазиоптимальности для случаев выпуклых дискретного и непрерывного множеств .
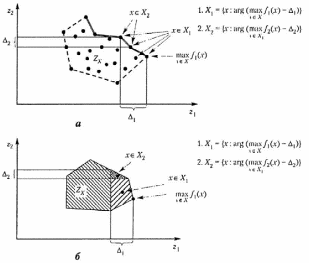
Рис. 2.22. Примеры применения лексикографического принципа квазиоптималыюсти для выпуклых дискретного (а) и непрерывного (б) множеств
Описанные главные принципы оптимальности могут быть использованы при постановке задач оптимизации для перехода от множества критериев к единому критерию и получения в результате этого перехода традиционной однокритериальной задачи для оптимизации. Правильное и гибкое использование данных принципов не означает их обязательного прямого использования иа стадии постановки задачи оптимизации. Предполагается их последовательное или комбинированное применение, исследование того, как изменяется при этом решение и как они согласуются с целями ЛПР.
Следует также отметить, что многие из принципов требуют от ЛПР дополнительной информации, которую ему обычно трудно предоставить априори. Зачастую ЛПР понимает то, чего можно достигнуть, только в процессе решения задачи. Фактически выбор того или другого принципа оптимальности не является математической проблемой, а выбор или построение принципа оптимальности должны вести к решению, удовлетворяющему требованиям ЛПР, и отражать представление его о качестве решения. Чем больше вариантов постановок задач оптимизации и их решений рассматривается ЛПР, тем больше шансов найти решение, полностью удовлетворяющее ЛПР.
Таким образом, важной рекомендацией по использованию принципов оптимальности может быть их комбинирование и разумное сочетание их применения в диалоге с ЛПР.