4.2.2. Затухающие колебания и их характеристики

Реальный колебательный контур всегда обладает активным сопротивлением R . Вследствие этого часть энергии электромагнитных колебаний превращается в тепло, а амплитуда колебаний постепенно уменьшается.

Дифференциальное уравнение затухающих колебаний на основании(4.65) и с учётом, что , , , принимает вид

. (4.73)

После замены

(4.74)

получим стандартное дифференциальное уравнение, описывающее затухающие колебания

. (4.75)

Здесь – коэффициент затухания, ω₀ – собственная частота свободных незатухающих колебаний (т.е. при R=0). Решение дифференциального уравнения (4.75) имеет вид

, (4.76)

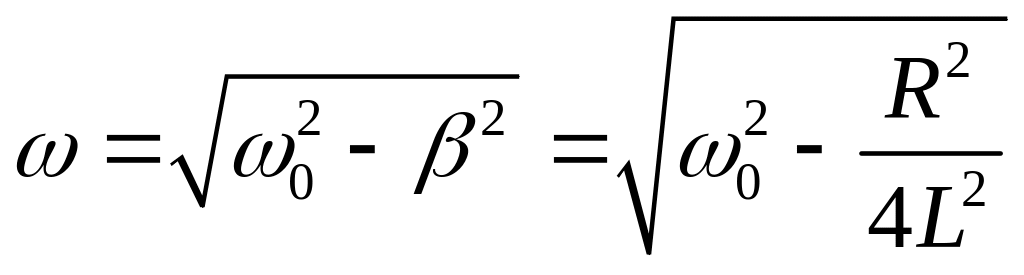где - частота затухающих колебаний в реальном контуре.

График затухающих колебаний представлен на рис.4.17. Амплитуда колебаний в этом случае изменяется по экспоненциальному закону

, (4.77)

а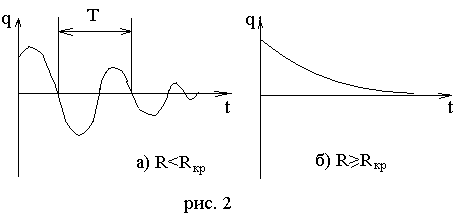 период колебаний определяется

выражением

. (4.78)

R<R_кр

Рис.4.17.

С увеличением R, а следовательно, и β, период затухающих колебаний растёт, стремясь к бесконечности при

. (4.79)

R>R_кр

Это означает, что при

колебательный разряд переходит в

апериодический процесс (рис.4.18).

Значение R_кр называется

критическим сопротивлением.

Важнейшей характеристикой контура является его добротность. При малых значениях логарифмического декремента затухания, добротность контура определяется выражением:

. (4.80)

4.2.3. Вынужденные колебания в контуре. Резонанс

Для осуществления вынужденных электромагнитных колебаний нужно включить последовательно с элементами контура источник переменного напряжения, изменяющегося по гармоническому закону.

U = U₀ cosω_в t . (4.81)

Тогда формула (4.65) примет вид

. (4.82)

Произведя преобразования, получим дифференциальное уравнение вынужденных электромагнитных колебаний

. (4.83)

В случае установившихся колебаний дифференциаль- ное уравнение имеет решение

q = q₀ cos(ω_в t + ψ), (4.84)

Следовательно, в установившемся режиме, вынужденные колебания происходят с частотой вынуждающего напряжения ω_в и являются гармоническими, амплитуда и фаза которых определяется выражениями

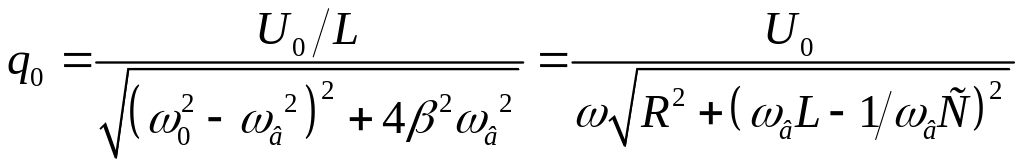, (4.85)

. (4.86)

Резонансные кривые для заряда (напряжения на конденсаторе) аналогичны резонансным кривым при механических колебаниях (см. рис. 1.13), а резонансная частота определяется по формуле (4.50).

Продифференцировав (4.85) по t, найдем силу тока в контуре

I = - q₀ ω_в sin(ω_в t + ψ) = I₀ cos(ω_в t + ψ + π/2),

где I₀ = q₀ ω_в – амплитуда тока.

Запишем это выражение в виде

I = I₀ cos(ωt – φ), (4.87)

где φ = -(ψ + π/2) – сдвиг фаз между током и приложенным напряжением.

Тогда в соответствии с (4.86) и (4.87)

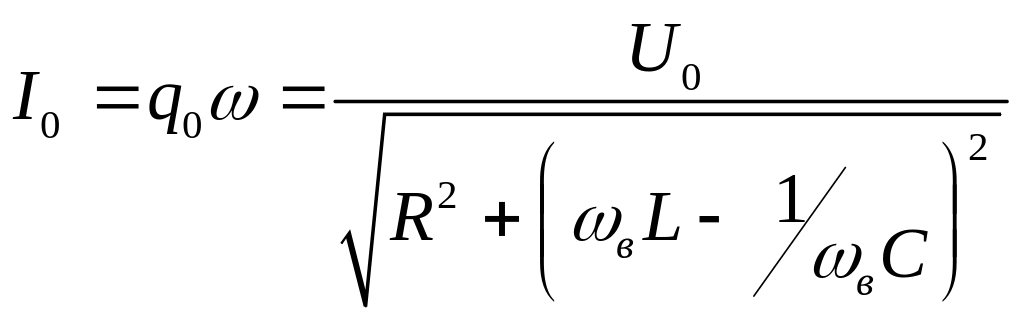, (4.88)

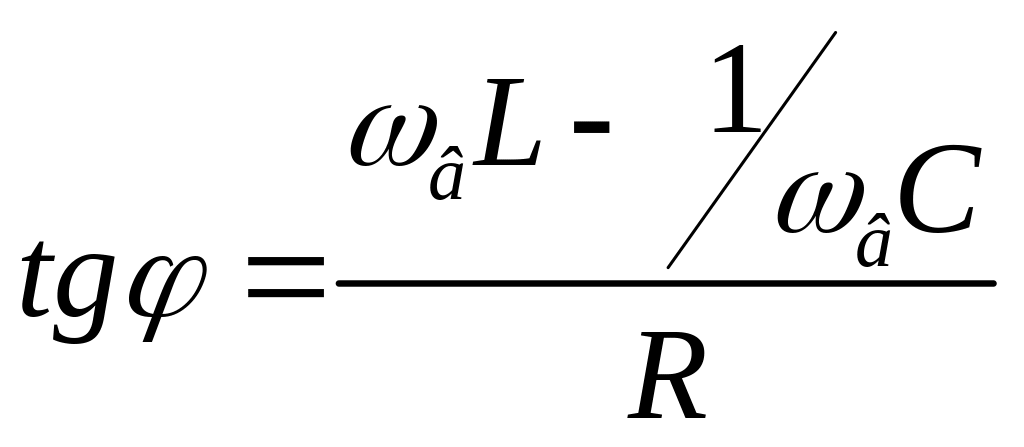. (4.89)

Из формулы (4.89) следует, что ток отстаёт по фазе от вынуждающего напряжения в том случае, когда , и опережает, когда . При условии сдвиг фаз равен нулю, а амплитуда тока достигает максимального значения.

Кривую зависимости амплитуды тока от частоты внешнего напряжения называют резонансной кривой. На рис. 4.19 даны резонансные кривые для силы тока при различных активных сопротивлениях контура. Чем меньше сопротивление контура R, тем больше амплитуда тока при резонансе и тем острее резонансная кривая.

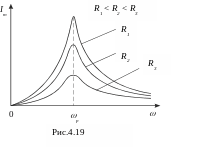
Резонансная частота для силы тока контура определяется соотношением

, (4.90)

а амплитуда тока при резонансе равна