
- •Часть 3
- •Занятие №14. Элементы математической статистики
- •14.1. Основные определения
- •14.2. Графическое представление выборки
- •14.3. Эмпирическая функция распределения (эфр)
- •Занятие №15. Статистическая оценка неизвестных параметров распределения. Точечные оценки
- •15.1. Постановка задачи
- •15.2. Основные свойства точечных статистических оценок распределения
- •15.3. Статистическая оценка мо
- •15.4. Статистическая оценка дисперсии
- •Исправленная дисперсия
- •15.5. Метод моментов
- •15.6. Метод максимального правдоподобия
- •Из первого уравнения находим . Подставив это значение во второе уравнение, получим . Заметим, что оценка совпадает с оценкой, полученной по методу моментов, а оценка не совпадает.
- •16.2. Доверительный интервал для математического ожидания св X, распределенной по закону n(m, σ) при известном σ
- •16.3. Доверительный интервал для мо св X, распределенной по нормальному закону при неизвестном σ
- •16.4. Доверительный интервал для σ2 св X, распределенной по нормальному закону
- •Примеры для самостоятельного решения
- •Ответы:
- •Занятие № 17. Проверка статистических гипотез
- •Занятие № 18. Проверка гипотезы о виде распределения случайной величины. Критерий
- •Дополнение. Распределение
- •Библиографический список
- •Библиографический список……………...............53
- •Часть 3
- •394026 Воронеж, Московский просп., 14
16.2. Доверительный интервал для математического ожидания св X, распределенной по закону n(m, σ) при известном σ
Пусть CB X имеет нормальное распределение N(m,σ). Тогда доверительный интервал для параметра m по результатам выборки x1,x2,...,xn объемом п при условии, что дисперсия σ2 известна, а доверительная вероятность равна 1-α, имеет вид
![]() .
(16.3)
.
(16.3)
Здесь u1-α/2, квантиль стандартизованного нормального распределения, определяется как решение уравнения
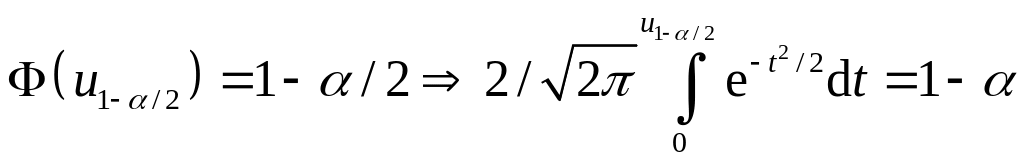 .
.
Для u1-α/2 имеется таблица
-
1-α
0,90
0,95
0,99
0,997
0,999
u1-α/2
1,64
1,96
2,58
3,00
3,37
Из анализа полученных соотношений можно сделать следующие выводы.
1. Увеличение объема п выборки приводит к уменьшению длины доверительного интервала.
2. Увеличение доверительной вероятности (1-α) приводит к увеличению длины доверительного интервала, то есть к уменьшению точности δ.
3.
Если
задать точность δ, то есть предельную
погрешность интервальной оценки, по
формуле (2) и доверительную вероятность
1-α, то из соотношения
![]() можно найти минимальный объем выборки,
который обеспечивает заданную точность:
можно найти минимальный объем выборки,
который обеспечивает заданную точность:
![]() .
.
16.3. Доверительный интервал для мо св X, распределенной по нормальному закону при неизвестном σ
Если
генеральная совокупность
![]() и
неизвестно, то с вероятностью
и
неизвестно, то с вероятностью
![]()
![]() ,
,![]() ,
(16.4)
,
(16.4)
![]() ,
,
где
![]() ,
,
![]()
![]() – квантиль распределения Стьюдента
(Пирсона) с
– квантиль распределения Стьюдента
(Пирсона) с
![]() степенью свободы уровня
степенью свободы уровня
![]() ,
–
объем выборки .
,
–
объем выборки .
Для нахождения квантилей распределения Стьюдента tp имеется таблица. Приведем ее для двух значений доверительной вероятности.
-
1-α n
5
10
20
30
∞
0,95
2,571
2,228
2,086
2,042
1,960
0,99
4,032
3,169
2,845
2,750
2,576
16.4. Доверительный интервал для σ2 св X, распределенной по нормальному закону
Пусть СВ X имеет нормальное распределение N(m,σ), причем m и σ неизвестны. Тогда доверительный интервал для параметра σ2 по выборке х1х2,..,xn объемом п с доверительной вероятностью 1-α имеет вид
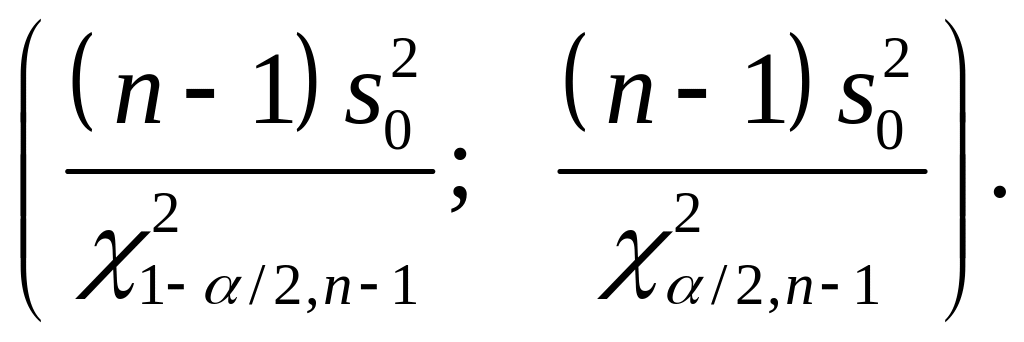 (16.5)
(16.5)
Для
квантилей
![]() имеются таблицы.
имеются таблицы.
Замечание.
Так как при п→∞
распределение
![]() приближается к нормальному, то при
достаточно большом объеме выборки
(п≥50)
доверительный интервал можно найти по
формуле
приближается к нормальному, то при
достаточно большом объеме выборки
(п≥50)
доверительный интервал можно найти по
формуле
![]() ,
,
где u1-α/2 квантиль стандартизованного нормального распределения, соответствующая доверительной вероятности 1-α.
Пример
16.1.
Измерения сопротивления резистора дали
следующие результаты (в омах):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Известно, что ошибки измерения имеют
нормальный закон распределения.
Систематическая ошибка отсутствует.
Построить доверительный интервал для
истинного сопротивления резистора с
надежностью 0,99 в предположении: а)
дисперсия ошибки измерения известна и
равна 4; б) дисперсия ошибки измерения
неизвестна.
.
Известно, что ошибки измерения имеют
нормальный закон распределения.
Систематическая ошибка отсутствует.
Построить доверительный интервал для
истинного сопротивления резистора с
надежностью 0,99 в предположении: а)
дисперсия ошибки измерения известна и
равна 4; б) дисперсия ошибки измерения
неизвестна.
Решение. В данной серии из девяти наблюдений
![]() .
.
Если
дисперсия ошибки измерения известна,
то можно воспользоваться формулой
(16.3). Для этого из таблицы функции Лапласа
(см. приложение) находим, что
![]() ,
т.е. уровню надежности 0,99 соответствует
значение
,
т.е. уровню надежности 0,99 соответствует
значение
![]() .
Тогда по формуле (16.3)
.
Тогда по формуле (16.3)
![]()
или
![]() с вероятностью 0,99.
с вероятностью 0,99.
В случае неизвестной дисперсии ее можно оценить на основе тех же опытных данных:
![]() ,
,![]() .По
таблице распределения Стьюдента (см.
приложение, табл. 3) для
.По
таблице распределения Стьюдента (см.
приложение, табл. 3) для
![]() степеней свободы и заданной вероятности
степеней свободы и заданной вероятности
![]() находим
находим
![]() .
Тогда по формуле (16.4)
.
Тогда по формуле (16.4)
![]()
или
![]() с вероятностью
с вероятностью
![]() .
.
Пример 16.2. В таблице приведены сгруппированные данные измерений роста у 50 наугад выбранных студентов:
-
Рост
166 – 170
170 – 174
174 – 178
178 – 182
182 – 186
186 – 190
Число
Студентов
3
7
15
13
11
1
Оценить средний рост и дисперсию роста студентов. Построить доверительный интервал для среднего роста студентов с надежностью 0,9.
Решение. Так как данные сгруппированы, то в качестве представителя каждого интервала можно взять середину этого интервала. Тогда
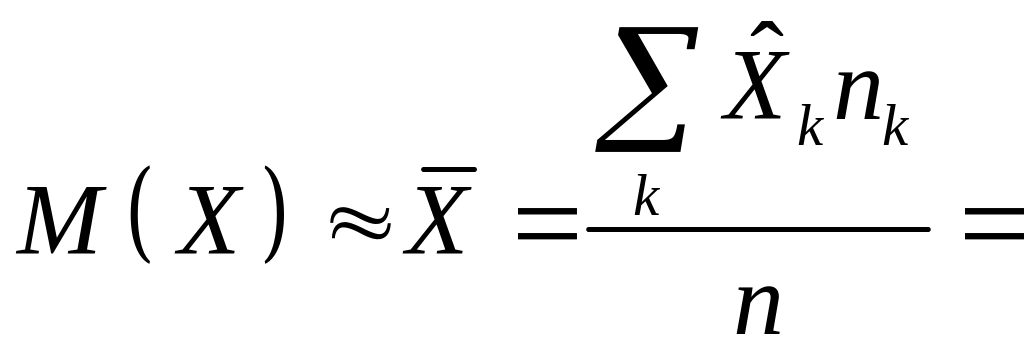
![]() ,
,

![]() ,
,
Так
как
![]() ,
то по формуле (16.4) имеем
,
то по формуле (16.4) имеем
![]()
или
![]() с вероятностью 0,9.►
с вероятностью 0,9.►
Пример
16.3. По
результатам девяти измерений емкости
конденсатора получена оценка
![]() мкФ. Среднеквадратическая ошибка
измерения известна и равна 0,04 мкФ.
Построить доверительный интервал для
емкости конденсатора с надежностью
0,95.
мкФ. Среднеквадратическая ошибка
измерения известна и равна 0,04 мкФ.
Построить доверительный интервал для
емкости конденсатора с надежностью
0,95.
Решение.
В предположении, что ошибки измерения
имеют нормальный закон распределения
можно воспользоваться формулой (16.3).
Так как
![]() ,
то
,
то
![]()
или
![]() с вероятностью 0,95.
с вероятностью 0,95.
вероятности 1-α.
