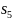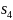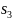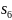2.2.3. Эквивалентные состояния автоматов

Пусть дан автомат . Требуется построить новый автомат , который:

1) покрывает (возможно, даже, эквивалентен ему);

2) имеет наименьшее число состояний среди всех автоматов, покрывающих . Считается, что функции φ и ψ всюду определены.

Далее следует определить эквивалентные друг другу состояния автомата . Затем следует склеить все эквивалентные состояния в одно.

Определение. Состояния автоматов и называются r-эквивалентными, если для любой входной строки длины r ( ) имеет место 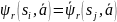. В этом случае используется запись . Если это не так, то используется запись . Если для любого r, то говорят, что состояния и эквивалентны и записывают .

Отношения E_r и E представляют собой отношения эквивалентности. Классы эквивалентности отношения E₁ являются множествами всех пар состояний, перерабатывающих каждый входной символ в фиксированный выходной символ. То есть запись 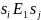означает, что

.

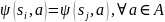В этом равенстве легко убедиться по таблице состояний.

Например, для автомата, заданного таблицей состояний:

Таблица 7

Текущее состояние	φ
	0	1	0	1
			0	1
			1	0
			0	1

В данном случае имеем 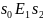. Таким образом, отношение эквивалентности 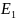состоит из следующих элементов:

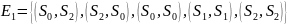
Дополнение отношения обозначается как . Тогда запись 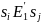означает, что 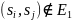. Таким образом:

Задача минимизации сводится к определению попарно эквивалентных состояний и последующему их склеиванию. При этом, оказывается эффективнее всего выявить в начале неэквивалентные состояния.

Вводятся функции φ^* и ψ^*

Определение: Функция 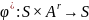, задаваемая выражением

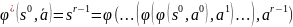
указывает на то, что –есть конечное состояние, в которое переходит автомат, начав работу из состояния s₀ и считав строку длины r.

Определение: Функция 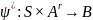, задаваемая выражением

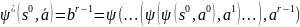
указывает на то, что - есть последний символ выходной строки, которую печатает автомат, начав работу из состояния s₀ и считав строку длины r.

Например, для первого автомата, изображенного на рисунке ( ) при 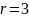имеем:

.

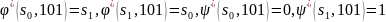2.3. Процедура минимизации конечных автоматов

Процедура минимизация основана на рассмотрении отношений эквивалентности между упорядоченными парами состояний конечного автомата.

Рассмотрим таблицу состояний автомата.

Таблица 8

Текущее состояние
				1	0	0
				0	1	1
				1	0	0
				0	1	1
				1	0	0
				0	1	1
				1	0	0
				1	0	0
				0	1	1

Таблица состояний автомата, подлежащего минимизации.

Начнем с нахождения отношений и . В соответствии с функцией , находим первое разбиение

. (1)

Оно разбивает состояния автомата на два класса эквивалентности и 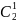(здесь вместо пишется 1, вместо пишется 2 и т.д.). Так как отношение рефлексивно и симметрично, то его всегда можно восстановить по множеству тех пар , для которых выполняется условие 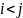, Обозначим это множество через 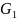. В общем случае обозначим через 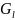множество упорядоченных пар 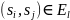, со свойствами . Для разбиения имеем:

={(1,3), (1,5), (1,7), (1,8), (3,5), (3,7), (3,8), (5,7), (5,8), (7,8,), (2,4), (2,6), (2,9), (4,6), (4,9), (6,9)},

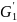={(1,2), (1,4), (1,6), (1,9), (2,3), (3,4), (3,6), (3,9), (2,5), (4,5), (5,6), (5,9), (2,7), (4,7), (6,7), (7,9), (2,8), (4,8), (6,8), (8,9)}.

Здесь и – классы эквивалентности относительно отношения . Следовательно, справедливы утверждения: 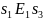, , 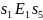а также , 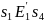и т.д.

Множество 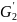состоит из элементов множества и ещё пар (2,9), (4,9) и (6,9). Это связано, например, с тем, что входной символ a₃, в соответствии с функцией , переводит упорядоченную пару состояний (2,9) в (4,7), а эта последняя пара принадлежит . Следовательно, пару (2,9) необходимо удалить из и добавить в . Добавление всех вышеуказанных пар к , определяет новое разбиение на классы эквивалентности:

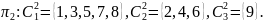(2)

Определим теперь множество . Оно состоит из элементов множества и ещё двух пар (2,6) и (4,6). Например, переводит (2,6) в (4,9), а эта последняя пара принадлежит . Поэтому разбиении 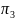имеем следующие классы эквивалентности:

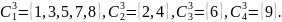(3)

Дальнейший перебор показывает, что 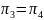, и, следовательно, .

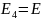Конструкция покрывающего автомата получается следующей. Каждый класс эквивалентности последнего разбиения становится состоянием нового автомата. Например, 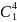обозначается чер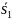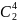ез , через 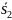и т.д. Получается автомат с 5-ю состояниями, покрывающий первоначальный автомат с 9-ю состояниями. Так как выходы для каждого начального состояния в фиксированном классе эквивалентности не зависит от этого состояния при односимвольных входах, то в таблице состояний нового автомата выход прямо считывается с таблицы состояний первоначального автомата. 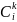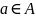Чтобы построить функцию перехода в следующее состояние, выберем по одному состоянию в каждом классе , и если элемент переводит в некоторое состояние из , то положим . Заметим, что это предписание однозначно: все 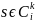переходят в состояния из после считывания .

Результат этой процедуры, примененной к автомату с табл. 8, показан на табл. 9. Получен минимальный автомат.

Таблица 9

Текущее состояние	Следующее состояние			Выход
				1	0	0
				0	1	1
				1	0	0
				0	1	1
				0	1	1

Минимальный автомат, покрывающий автомат с табл. 8.

Практически необязательно перечислять все пары из и 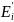. Достаточно на каждом шаге смотреть, переводит ли некоторый входной символ 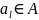пару 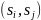в разные классы эквивалентности и . Если да, то на следующем шаге состояния и следует разнести по разным классам.

Пример.

Рассмотрим автомат с пятью состояниями:

Таблица 10

Текущеесостояние	Следующее состояние		Выход
	0	1	0	1
s0	s1	s2	1	0
s1	s4	s2	0	0
s2	s3	s0	1	0
s3	s4	s0	0	0
s4	s4	s4	0	0

По выходной функции определяем, что:

.

Это приводит к разбиению

.

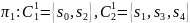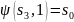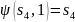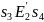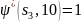В соответствии с функцией входной символ 1 переводит состояние в , т.е. , кроме того, . Однако , так что (ибо и ).

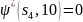Следующее разбиение π₂состоит из классов эквивалентности

.

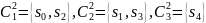Дальнейшего измельчения не происходит, ибо переводит каждый элемент класса эквивалентности в один и тот же класс. Итак, состояния и можно склеить в одно состояние 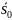, а состояния и – в состояние . Состояние получает новое обозначение . Новый минимальный автомат, покрывающий исходный автомат:

Таблица 11

Текущеесостояние	Следующее состояние		Выход
	0	1	0	1
			1	0
			0	0
			0	0