
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
Литература: [1], c. 56-66.
Указание. Перед изучением этой темы повторите все виды уравнений первого порядка и способы их решения.
Основные понятия
В некоторых частных случаях удается понизить порядок дифференциального уравнения второго порядка. Зачастую оно в итоге приводится к дифференциальному уравнению первого порядка одного из изученных ранее типов. Рассмотрим наиболее типичные случаи.
I. Уравнения вида
Интегрированием
обеих частей уравнения
оно приводится к уравнению первого
порядка
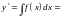
 .
Повторно интегрируя полученное уравнение,
находим общее решение исходного уравнения
.
Повторно интегрируя полученное уравнение,
находим общее решение исходного уравнения
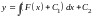 .
.
Заметим,
что аналогично решаются уравнения
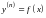 .
.
II. Уравнения вида , явно
не
содержащие искомой функции
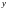
Такие
уравнения допускают понижение порядка
подстановкой
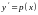 ,
,
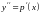 .
Другими словами, данное уравнение
равносильно системе дифференциальных
уравнений первого порядка
.
Другими словами, данное уравнение
равносильно системе дифференциальных
уравнений первого порядка
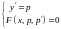 .
.
Аналогично
решаются уравнения вида
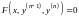 .
.
III. Уравнения вида , явно
не содержащие независимой переменной
Уравнения
такого вида допускают понижение порядка
подстановкой
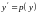 ,
,
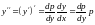 .
Таким образом, данное уравнение
равносильно системе дифференциальных
уравнений первого порядка
.
Таким образом, данное уравнение
равносильно системе дифференциальных
уравнений первого порядка
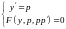 .
.
Дифференциальные
уравнения
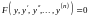 допускают понижение порядка такой же
подстановкой:
допускают понижение порядка такой же
подстановкой:
,
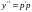 ,
,
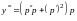 и т.д.
и т.д.
Контрольные вопросы и задания
1. Какие уравнения второго порядка приводятся к уравнениям первого порядка?
2. Как решаются уравнения вида ?
3. Как решаются уравнения вида ?
4. Как решаются уравнения вида ?
5. Как решаются уравнения вида ?
6. Как решаются уравнения вида ?
7. Можно ли понизить порядок дифференциального уравнения вида ?
Примеры решения задач
Пример
1. Найти
частное решение дифференциального
уравнения
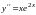 ,
удовлетворяющее заданным начальным
условиям
,
удовлетворяющее заданным начальным
условиям
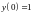 ,
,
 .
.
Решение.
Интегрируя левую и правую части, находим
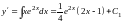 .
Повторное интегрирование приводит к
общему решению
.
Повторное интегрирование приводит к
общему решению
 .
Учитывая начальные условия, записываем
систему уравнений для определения
постоянных
.
Учитывая начальные условия, записываем
систему уравнений для определения
постоянных
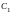 и
и
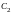 :
:
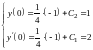
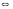
 .
.
Подставляя найденные значения постоянных в общее решение уравнения, получаем искомое частное решение
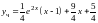 .
.
Пример
2. Решить
уравнение
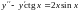 .
.
Решение.
Данное уравнение имеет вид
.
Положим
.
Тогда
.
Получаем дифференциальное уравнение
первого порядка
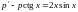 – линейное относительно неизвестной
функции
– линейное относительно неизвестной
функции
 .
Его общее решение
.
Его общее решение
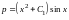 ,
т.е.
,
т.е.
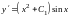 .
Интегрируя это равенство, найдем общее
решение исходного уравнения
.
Интегрируя это равенство, найдем общее
решение исходного уравнения
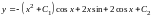 .
.
Пример
3. Найти
частное решение дифференциального
уравнения
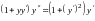 ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
 .
.
Решение.
Данное уравнение имеет вид
.
Подстановка
,
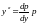 приводит его к виду
приводит его к виду
 ,
откуда
,
откуда
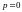 ,
т.е.
,
т.е.
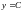 (это решение не удовлетворяет начальным
условиям), или
(это решение не удовлетворяет начальным
условиям), или
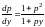 .
Полученное дифференциальное уравнение
первого порядка не относится к уравнениям
известного нам типа. Перепишем его в
виде
.
Полученное дифференциальное уравнение
первого порядка не относится к уравнениям
известного нам типа. Перепишем его в
виде
 .
Это линейное уравнение относительно
функции
.
Это линейное уравнение относительно
функции
 .
Его общее решение имеет вид
.
Его общее решение имеет вид
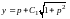 .
Теперь необходимо решить дифференциальное
уравнение
.
Теперь необходимо решить дифференциальное
уравнение
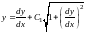 .
Но в общем виде решить его достаточно
сложно. Так как нам нужно найти частное
решение исходного уравнения, то
воспользуемся начальными условиями
для определения постоянной
,
полагая в последнем равенстве
.
Но в общем виде решить его достаточно
сложно. Так как нам нужно найти частное
решение исходного уравнения, то
воспользуемся начальными условиями
для определения постоянной
,
полагая в последнем равенстве
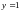 и
и
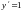 .
Приходим к равенству
.
Приходим к равенству
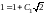 ,
из которого
,
из которого
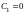 .
Таким образом, нам достаточно решить
уравнение
.
Таким образом, нам достаточно решить
уравнение
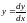 ,
откуда
,
откуда
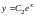 .
Учитывая начальное условие
,
находим
.
Учитывая начальное условие
,
находим
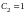 и записываем искомое частное решение
и записываем искомое частное решение
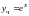 .
.
Задачи и упражнения для самостоятельного решения
Решить задачи: №№ 4155, 4156, 4160, 4161, 4165, 4166, 6470, 4178 [2].
Форма отчетности: устный опрос, контрольная работа, типовой расчет.
