4. Клики, независимые множества

Множество вершин графа называется независимым (внутренне устойчивым), если никакие две вершины из этого множества не смежны. Граф, порождённый вершинами независимого множества, является пустым.

Независимое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества.

Наибольшее по мощности независимое множество называется наибольшим.

Как установил К.Э. Шеннон, теория независимых множеств в графе имеет большое значение для фундаментальных проблем теории информации. Сам процесс передачи информации может быть представлен в виде графа, причём максимальное число безошибочных сигналов соответствует максимальному независимому множеству графа.

Число вершин в наибольшем независимом множестве графа G называется числом вершинной независимости (числом независимости) или неплотностью этого графа и обозначается . Для графа, изображённого на рис. 47, наибольшими независимыми множествами будут: и , максимально независимыми , и т.д.

Рис. 47

Задачи отыскания наибольшего независимого множества и определения числа независимости, как правило, очень трудны, поэтому полезны оценки их величин.

Теорема. Для любого графа G = (S,U) верно неравенство

Алгоритм построения независисимого множества.

Независимое множество M, такое, что строится следующим образом. Всякий раз в графе G выбирается вершина минимальной степени и заносится в множество M, после чего эта вершина и все смежные с ней удаляются из графа. Далее процесс повторяется. Построенное таким способом множество M иногда принимают в качестве первого приближения при отыскании наибольшего независимого множества вершин графа.

С понятием независимости в графе связано понятие доминирования. Подмножество вершин графа G = (S,U) называется доминирующим (внешне устойчивым), если каждая вершина из смежна с некоторой вершиной из , т.е. каждая вершина графа находится на расстоянии в одно ребро от доминирующего множества. Доминирующее множество называется минимальным, если никакое его собственное подмножество не является доминирующим. Доминирующее множество, имеющее наименьшую мощность, называется наименьшим.

Число доминирования графа G есть наименьшее число вершин, составляющих минимальное доминирующее множество. Отыскание наименьшего доминирующего множества является содержанием многих прикладных задач. Например, задача размещения предприятий в ряде населённых пунктов при условии, чтобы расстояние от каждого из населённых пунктов до какого-либо предприятия не превосходило заданной величины, сводится к построению наименьшего доминирующего множества, если предположить, что вершины графа – предприятия - смежны тогда и только тогда, когда расстояние между соответствующими пунктами не превышает заданной величины.

Теорема. Независимое множество максимально тогда и только тогда, когда оно доминирующее.

Антиподом понятия независимого множества является понятие клики. Подмножество вершин графа G = (S,U) называется кликой, если любые две входящие внего вершины смежны. Это значит, что подграф является полным. Определение клик графа полезно при информационном поиске.

Клика называется максимальной, если она не содержится в клике с большим числом вершин, и наибольшей, если число вершин в ней наибольшее среди всех клик. Число вершин в наибольшей клике графа называется кликовым числом или плотностью графа и обозначается через

Теорема. Подмножество вершин графа G является кликой тогда и только тогда, когда оно независимо в дополнительном графе т.е.

Клика графа представляет «естественные» группировки вершин в максимально полные подграфы. На рис. 48 представлен граф и все его клики.

Рис. 48

Алгоритм выделения клик в графе.

Этот алгоритм представляет собой поиск с возвращением по специальному дереву поиска. Каждый узел этого дерева соответствует полному подграфу исходного графа, а само дерево поиска строится следующим образом. Корень дерева поиска – пустое начальное множество Пусть теперь S – произвольная вершина дерева поиска какого-либо уровня. Тогда вершиной следующего уровня дерева будет вершина если и смежна с каждой вершиной из S. В дереве поиска вершины S и соединяются ребром, которое соответствует вершине x. На рис. 49 показано дерево поиска для графа G, изображённого на рис. 48 (вершины обозначены только цифрами, буква x опущена).

S=

{4}

{1}

{2}

{3}

{5}

{6}

{8}

{7}

{1,2}

{2,1}

{2,8}

{3,2}

{3,8}

{3,6}

{3,5}

{4,6}

{4,5}

{5,4}

{5,3}

{5,6}

{6,5}

{6,7}

{6,4}

{7,6}

{7,3}

{8,3}

{2,3}

{3,7}

{6,3}

{8,2}

{5,4,6}

{5,6,4}

{6,5,3}

{3,6,5}

{4,6,5}

{3,7,6}

{3,2,8}

{2,3,8}

{6,7,3}

{6,3,7}

{7,6,3}

{8,3,2}

{5,3,6}

{5,6,3}

{3,5,6}

{4,6,5}

{3,6,7}

{3,8,2}

{3,8,3}

{6,5,4}

{6,3,5}

{6,4,5}

{7,3,6}

{8,2,3}

Рис. 49

Каждая клика мощностью n порождается в дереве поиска n! Раз. При построении дерева все тонкие рёбра можно оборвать, они не приводят к новым кликам. При этом необходимо руководствоваться двумя правилами.

1. Если все поддеревья узла в дереве поиска клик уже исследованы, то нужно исследовать лишь только те вершины из 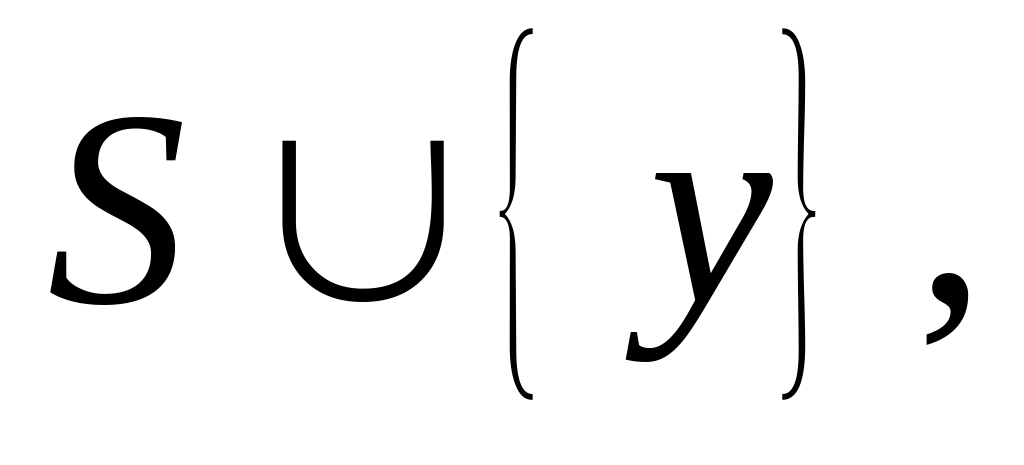для которых y не смежна с x.

2. Если S – узел в дереве поиска, а 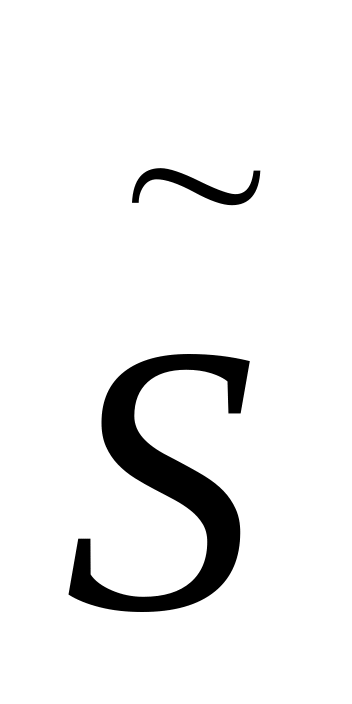- узел предыдущего уровня и все поддеревья узла уже исследованы, то все неисследованные поддеревья узла можно опустить.

Иногда полезно понятие матрицы клик. Пусть G = (S,U) - прозвольный граф, - множество всех его максимальных клик и . Определим бинарную -матрицу C = C(G), строки которой соответствуют кликам из множества Q, а столбцы – вершинам графа G, причём

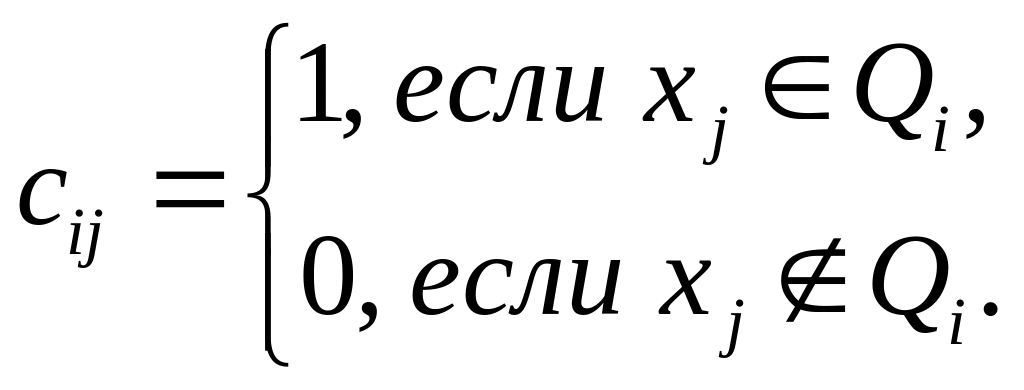
Матрица C(G) назавается матрицей клик графа G. Для графа, изображённого на рис. 48, матрица клик имеет следующий вид: