(Замкнутая система массового обслуживания)

Вероятность того, что в системе занято k обслуживающих аппаратов при условии, что число требований, находящихся в системе, не превосходит числа обслуживающих аппаратов, т.е. когда очереди нет:

Р_k =  ^k  Р₀, (0  k  n), (4.15)

где k– число требований; n – число обслуживающих аппаратов; m – наибольшее возможное число требований, находящихся в обслуживаемой системе одновременно.

Вероятность того, что в системе находится k требований для случая, когда их число больше числа обслуживающих аппаратов, т.е. когда есть очередь:

Р_k = ^k  Р₀, (n < k  m). (4.16)

Вероятность того, что все обслуживающие аппараты свободны:

Р₀ = ( ^k +  ^k)^-1. (4.17)

Введем обозначения для краткой записи ( ) и ( ), тогда

Р₀ = ( + )^-1. (4.18)

Среднее число требований, ожидающих начала обслуживания, т.е. средняя длина очереди

М₁ =  Р_k. (4.19)

Коэффициент простоя обслуживаемого требования в ожидании обслуживания

К₁ = . (4.20)

Среднее число требований, находящихся в обслуживающей системе, т.е. в очереди и в обслуживании

М₂ =  Р_k. (4.21)

Коэффициент простоя обслуживаемого требования в обслуживающей системе

К₂ = . (4.22)

Среднее число свободных обслуживающих аппаратов

М₃ =  Р_k. (4.23)

Коэффициент простоя обслуживающего аппарата

К₃ = . (4.24)

Пример. Два рабочих обслуживают группу из 9 станков. В среднем каждый станок останавливается один раз в час. Обслуживание одного станка занимает у рабочего в среднем 6 мин. Определить основные характеристики эффективности функционирования системы массового обслуживания.

Решение. n = 2, m = 9,  = 1, = 6 мин = 0,1 ч.,

 = = 10,  = = 0,1.

В любой момент времени система находится в одном из своих возможных состояний:

k = 0 – все станки работают, очереди нет;

k = 1 – один станок обслуживается, очереди нет;

k = 2 – два станка обслуживаются, очереди нет;

k = 3 – два станка обслуживаются, один в очереди, остальные работают;

…………………………..………………………………

k = 9 – два станка обслуживаются, семь в очереди на обслуживание, т.е. ни один станок не работает.

Этим состояниям системы соответствуют вероятности:

Р₀, Р₁, Р₂, Р₃, …, Р₉.

Определим значения для случая, когда очереди нет

(0  k  2):

₀ =  0,1 = 1; ₁ =  0,1¹ = 0,9; ₂ =  0,1² = 0,36.

Определим значения для случая, когда очередь есть

(3  k  9):

₃ =  0,1³ = 0,126; … ₉=  0,1⁹ = 0,0000014175.

Вероятность того, что в системе не будет ни одного требования:

Р₀ = (2,43545)^-1 = 0,4106.

Среднее число станков, стоящих в очереди:

М₁ =  Р_k = 0,098.

Это означает, что в среднем из 9 станков 0,098 простаивают в очереди на обслуживание.

Коэффициент простоя станка в очереди

К₁ = = 0,011.

Это означает, что в среднем каждый станок 1,1 % времени простаивает в очереди.

Среднее число простаивающих станков (в очереди и обслуживании)

М₂ =  Р_k = 0,907.

Это означает, что в среднем 95 % рабочего времени 1 станок из 9 не будет работать.

Коэффициент простоя станка в системе обслуживания

К₂ = = 0,1008.

Это означает, что 10,08 % времени в среднем будет простаивает каждый станок из 9.

Среднее число свободных обслуживающих аппаратов (рабочих)

М₃ =  Р_k = 1,1907.

Это означает, что из двух человек в среднем один всегда свободен, а другой свободен в течение 18,6 % времени.

Коэффициент простоя рабочего

К₃ = = 0,595.

Это означает, что в среднем каждый рабочий 59,5 % рабочего времени простаивает без работы.

Результаты расчетов представлены в таблице 4.2.

Для автоматизации расчёта характеристик многоканальной замкнутой системы массового обслуживания возможно использование программы «Теория массового обслуживания» из ППП PRIMA. Выбор вида модели осуществляется в закладке Параметры и завершается нажатием кнопки Выбор (рис. 60).

Рис. 60. Выбор модели СМО

Таблица 2.2

Число требований, k	Число требований, ожидающих обслуживания, k - n	Число свободных рабочих, n - k	и	Рk=kР0	(k-n) Рk	kРk	(n-k) Рk
0	-	2	1	0,4106	-	-	0,8212
1	-	1	0,9	0,3695	-	0,3695	0,3695
2	-	-	0,36	0,1478	-	0,2956	-
3	1	-	0,126	0,0517	0,0517	0,1551	-
4	2	-	0,0378	0,0155	0,031	0,062	-
5	3	-	0,00945	0,00388	0,01164	0,0194	-
6	4	-	0,00189	0,000776	0,003104	0,004656	-
7	5	-	0,0002835	0,0001164	0,000582	0,0008148	-
8	6	-	0,0002835	0,0000116	0,0000696	0,0000928	-
9	7	-	0,0000014175	0,0000005	0,0000035	0,0000045	-
	-	-	2,43545	-	0,098	0,907	1,1907

В качестве исходных данных многоканальной замкнутой модели СМО следует ввести интенсивность входного потока требований и интенсивность обслуживания, число каналов обслуживания и число источников требований (максимально возможное число заявок в системе (рис. 61).

Рис. 61. Ввод исходных данных СМО в диалоговую форму

Результаты расчёта характеристик замкнутой многоканальной системы массового обслуживания представлены на рис. 62.

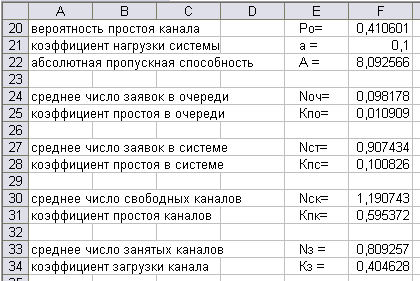
Рис. 62. Расчёт характеристик замкнутой СМО

Принятие решения о выборе оптимальной системы массового обслуживания требует многократного расчёта параметров системы массового обслуживания при изменении значений исходных данных. Выбор оптимального (рационального) варианта осуществляется согласно принятому критерию эффективности. Так, величина затрат, связанных с пребыванием в очереди одного требования (заявки) имеет вид

,

где С - величина затрат, связанных с пребыванием в очереди одного требования, ден.ед./час; n – число каналов обслуживания;  - интенсивность входного потока, заявок/час; С_оч –издержки, связанные с пребыванием в очереди одного требования, ден.ед./час; t_оч – среднее время ожидания в очереди, час; С_об – затраты на содержание обслуживающего устройства (канала).