6.5. Наибольшее и наименьшее значения функции на отрезке

Пусть функция непрерывна на отрезке . Как извест­но, такая функция достигает своих наибольшего и наименьшего значе­ний. Эти значения функция может принять либо во внутренней точке отрезка , либо на границе отрезка, т.е. при или . Если , то точку следует искать среди критических точек данной функции (см. рис. 6.12).

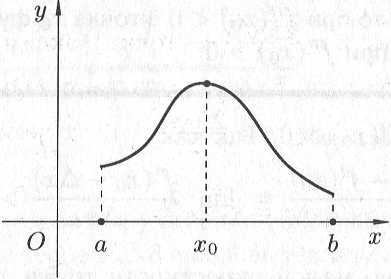
Рис. 6.12

Получаем следующее правило нахождения наибольшего и наи­меньшего значений функции на :

1. найти критические точки функции на интервале ;

2. вычислить значения функции в найденных критических точках;

3. вычислить значения функции на концах отрезка, т. е. в точках и ;

4. среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Замечания: 1. Если функция на отрезке имеет лишь одну критическую точку и она является точкой максимума (мини­мума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке 6.12 (нб — наибольшее, max — максимальное).

2. Если функция на отрезке не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение ( ) функция при­нимает на одном конце отрезка, а наименьшее ( ) — на другом.

Пример 6.10. Найти наибольшее и наименьшее значения функ­ции на отрезке .

Решение: Находим критические точки данной функции:

;

при и при . Находим , , , . Итак, в точке , в точке .

Нахождение наибольшего и наименьшего значений функции широ­ко применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин.

Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и другие зада­чи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольших и наименьших значений. Решением таких задач занимается особая ветвь математи­ки — линейное программирование.

Рассмотрим более простую задачу.

Пример 6.11. Из шара радиуса выточить цилиндр наиболь­шего объема. Каковы его размеры?

Решение: Обозначим через и высоту и диаметр цилиндра. Тогда, как видно из рисунка 153, , а потому объем цилиндра

,

Рис. 6.13

Находим наибольшее значение функции на промежутке . Так как , то при , кроме того, . Поэтому — точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный ) при диаметр основания

цилиндра равен

.

Таким образом, искомый цилиндр имеет высоту, равную , и диаметр, равный .

6.6. Выпуклость графика функции. Точки перегиба

График дифференцируемой функции называется выпу­клым вниз на интервале , если он расположен выше любой ее касательной на этом интервале. Гра­фик функции называется выпуклым вверх на интервале , если он расположен ниже любой ее касатель­ной на этом интервале.

Точка графика непрерывной функ­ции , отделяющая его части раз­ной выпуклости, называется точкой пе­региба.

На рисунке 6.14 кривая вы­пукла вверх в интервале , выпукла вниз в интервале , точка — точка перегиба.

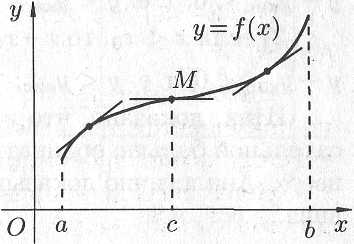
Рис. 6.14

Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы.

Теорема 6.11. Если функция во всех точках интервала имеет отрицательную вторую производную, т.е. , то график функции в этом интервале выпуклый вверх. Если же — график выпуклый вниз.

Доказательство. Пусть . Возьмем на графике функции произ­вольную точку с абсциссой и проведем через касатель­ную (см. рис. 6.15). Покажем, что график функции расположен ниже этой касательной.

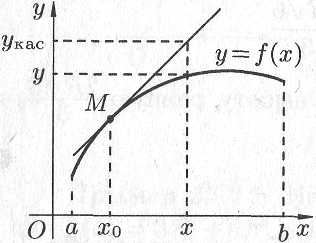
Рис. 6.15

Для этого сравним в точке ординату кривой с ординатой ее касательной. Уравнение касательной, известно, есть

, т.е. .

Тогда . По теореме Лагранжа, , где лежит между и . Поэтому

,

т.е.

.

Разность снова преобразуем по формуле Лагранжа:

,

где лежит между и . Таким образом, получаем

.

Исследуем это равенство:

1) если , то , и . Следовательно, , т.е. :

2) если , то , и . Следовательно, , т.е. :

Итак, доказано, что во всех точках интервала ордината касательной больше ординаты графика, т.е. график функции выпуклый вверх. Аналогично доказывается, что при график выпуклый вниз.

Для нахождения точек перегиба графика функции используется следующая теорема.

Теорема 6.12 (достаточное условие существования точек пере­гиба). Если вторая производная при переходе через точку , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой есть точка перегиба.

Доказательство. Пусть при и при . Это значит, что слева от график выпуклый вверх, а справа — выпуклый вниз. Следовательно, точка графика функции является точкой' перегиба.

Аналогично доказывается, что если при и при , то точка — точка перегиба графика функция .

Пример 6.12. Исследовать на выпуклость и точки перегиба график функции .

Решение: Находим, что , . Вторая производная существует на всей числовой оси; при .

Отмечаем, что при ; при .

Следовательно, график функции в интервале — выпуклый вверх, в интервале — выпуклый вниз. Точ­ка есть точка перегиба.