2.3. Сингулярный спектральный анализ временного ряда

Сингулярный спектральный анализ зародился в 70х-80х годах прошлого столетия из теории динамических систем. В его основе лежит трансформация временного ряда в матрицу и ее сингулярное разложение [23]. После идентификации компонент сингулярного разложения происходит их группировка, приводящая к разложению исходного ряда на аддитивные компоненты, такие как тренд, колебания (периодики) и шум. При этом метод не требует стационарности ряда, знания модели тренда, а также сведений о наличии в ряде периодических составляющих и их периодах. Также с помощью данного метода можно определить модель тренда и использовать это знание для дальнейшей обработки ряда уже с известной моделью тренда. В зарубежной литературе метод наиболее известен под названием SSA (SingularSpectrumAnalysis).

Математической основой метода SSA является сингулярное разложение [20]. Для успешного применения метода SSA следует последовательно пройти несколько шагов. Пусть имеется вещественнозначный временной ряд F = (f_o,…,f_N-1) длины N, N > 2. Алгоритм можно разбить на четыре шага: вложение, сингулярное раз­ложение, группировка и диагональное усреднение. Первые два в совокуп­ности называются разложением, последние - восстановлением. Основным параметром алгоритма служит так называемая длина окна L, 1 <L< N. Ре­зультатом алгоритма является разбиение временного ряда на аддитивные составляющие.

Первым шагом является процедура вложения, которая переводит исходный временной ряд в по­следовательность многомерных векторов.

Пусть L — некоторое целое число (длина окна), 1 <L< N. Процедура вложения образует K = N — L +1 векторов вложения

имеющих размерность L.

L – траекторная матрица ряда F

состоит из векторов вложения в качестве столбцов.

Другими словами, траекторная матрица — это матрица

.

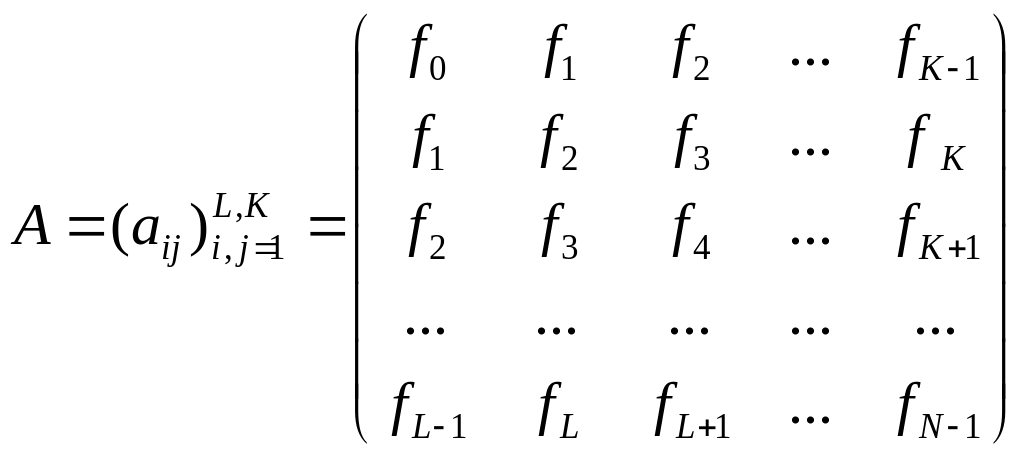Очевидно, что a_ij = f_i+j-2 и матрица X имеет одинаковые эле­менты на «диагоналях» i + j =const. Таким образом, траекторная матрица является ганкелевой. Существует взаимно-однозначное со­ответствие между ганкелевыми матрицами размерности и рядами длины N = L + K- 1.

Из-за того, что нет общих рекомендаций по выбору ширины окна, параметр L зависит от решаемой задачи и предварительной информации, известной о ряде. Например, для выделения тренда рекомендуется выбирать ширину окна не слишком большой. С другой стороны, для выделения гармонических колебаний рекомендуется большая ширина окна.

Далее проводится сингулярное разложение матрицы A. Обозначим . Матрица симметричная и неотрицательно определенная, а значит ее собственные числа вещественны и неотрицательны. Представленные в виде собственные числа называют сингулярными значениями матрицы А. Пусть – соответствующие им ортонормированные собственные вектора. Будем называть порядком сингулярного разложения. Обозначим

. (2) Тогда сингулярным разложением матрицы A называется ее представление в виде суммы элементарных матриц

. (3)

Каждая из матриц имеет ранг, равный единице. Поэтому их можно назвать элементарными матрицами. Вектор называют k-м левым сингулярным вектором или просто k-м собственным вектором, вектор – правым сингулярным вектором.

Набор будем называть k-ой собственной тройкой.

Этап группировки. Вид левых и правых сингулярных векторов, трактуемых в SSA как временные ряды, является очень важным для следующего шага метода – группировки [4]. При этом для одномерного SSA левые и правые сингулярные вектора обладают определенной симметрией, так как в этих случаях сингулярные разложения траекторных матриц с длиной окна и эквивалентны.

Процедура группировки формально одинакова для всех разновидностей SSA. На основе разложения (3) процедура группировки делит все множество индексов на непересекающихся подмножеств .

Пусть Тогда результирующая матрица , соответствующая группе , определяется как .Такие матрицы вычисляются для , тем самым разложение (3) может быть записано в сгруппированном виде:

.

Процедура выбора множеств и называется группировкой собственных троек.

Этап диагонального усреднения. На последнем шаге базового алгоритма каждая матрица сгруппированного разложения переводится в новый ряд длины . Для произвольной матрицы X процедуру приведения ее к ганкелевому виду и последующему преобразованию в ряд (обозначим его как G^в) выразим следующим образом. Пусть – матрица размера с элементами , , . Положим , и . Пусть , если и в остальных случаях. Тогда диагональное усреднение переводит матрицу в ряд по формуле

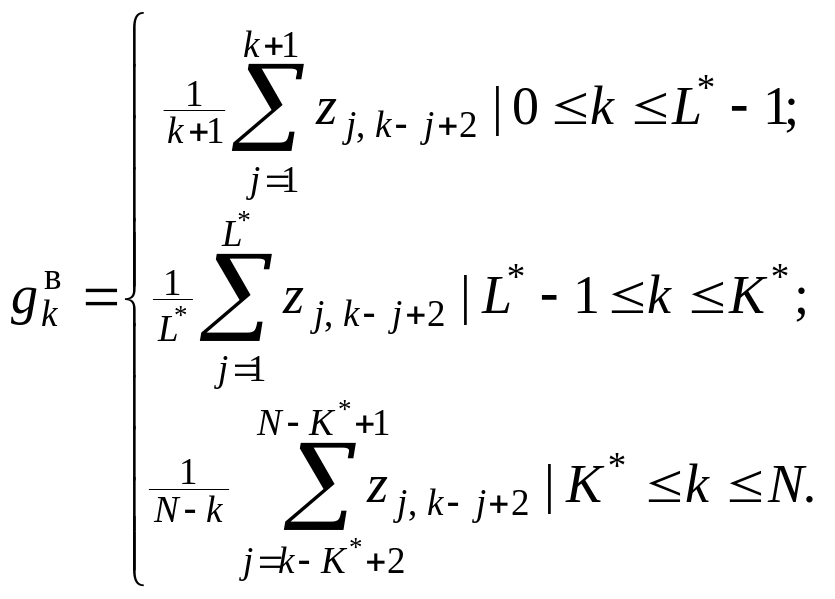
Это выражение соответствует усреднению элементов матрицы вдоль побочных диагоналей : выбор дает , для получаем и т. д. Применив диагональное усреднение к матрицам, полученным на этапе группировки, приходим к разложению исходного ряда в сумму рядов [21].