Основные типы отношений

Ключевые слова: рефлексивность, симметричность, транзитивность, отношение эквивалентности, фактор-множество, отношение частичного порядка, диаграмма Хассе.

Задача 3.1. Определите свойства отношения , матрица которого имеет вид

.

Решение. Заметим, что на главной диагонали матрицы стоят все единицы, следовательно, рефлексивное отношение, т.е. . Матрица несимметрична, тогда несимметрично отношение . Проверим антисимметричность. Для этого найдем

.

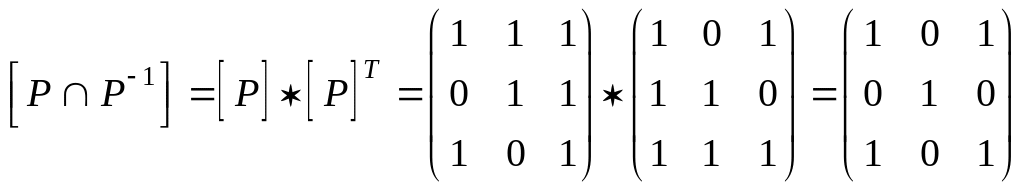Так как не все элементы, стоящие вне главной диагонали, нулевые, то отношение не является антисимметричным. Проверим транзитивность.

Вычислим

.

Так как , то отношение нетранзитивно.

Задача 3.2. Докажите, что если и - симметричные отношения, то также симметричное отношение.

Решение. Чтобы доказать симметричность, рассмотрим элемент и покажем, что элемент также принадлежит этому отношению. Итак,

,

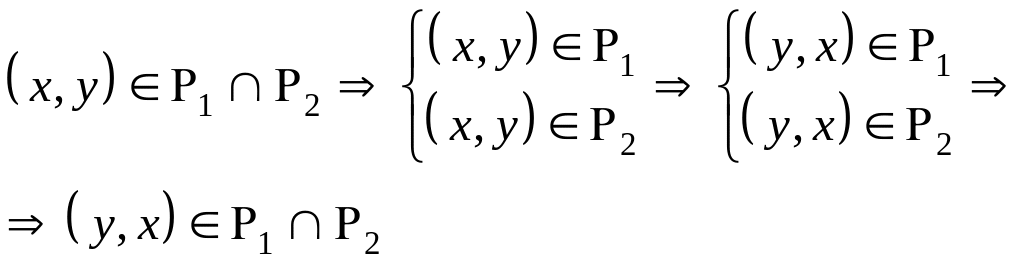что и требовалось доказать.

Задача 3.3. Пусть отношение задано следующим образом:

.

Определите свойства этого отношения.

Решение. Отношение рефлексивно, так как если , то для , и, следовательно .

Отношение симметрично. Предположим, что , тогда существует целое число такое, что и

для целого числа . Таким образом, .

Проверим транзитивность . Предположим, что - целые числа и и . По определению

, тогда для некоторого целого числа ,

, тогда для некоторого целого числа .

Суммирование левых и правых частей этих двух равенств дает

для некоторого целого числа . По определению , поэтому транзитивно. Поскольку рефлексивно, симметрично и транзитивно, то оно является отношением эквивалентности.

Найдем классы эквивалентности . Класс эквивалентности, порожденный элементом в данном случае определяется следующим образом:

=

.

Таким образом, получаем следующие классы эквивалентности:

,

,

,

,

Заметим, что элементы «похожи» в том смысле, что каждый из них кратен 5. Элементы любого другого класса эквивалентности «похожи» в том смысле, что имеют один и тот же остаток при делении на пять.

Фактор-множество множества целых чисел по отношению эквивалентности имеет вид

.

Задача 3.4. Отношение , задано матрицей, которая имеет вид

	1	0	0	1	0	0
	0	1	0	0	0	0
	0	0	1	0	1	1
	1	0	0	1	0	0
	0	0	1	0	1	1
	0	0	1	0	1	1

Определить классы эквивалентности.

Решение. Переставляя строки и столбцы, матрицу отношения можно привести к блочно-диагональному виду, а значит является эквивалентностью, и по полученной матрице можно определить классы эквивалентности .

	1	1	0	0	0	0
	1	1	0	0	0	0
	0	0	1	0	0	0
	0	0	0	1	1	1
	0	0	0	1	1	1
	0	0	0	1	1	1

Таким образом, . Таким образом, фактор-множество множества по отношению эквивалентности имеет вид

.

Задача 3.5. Определите тип отношения

.

Решение. Элементы этого отношения будут упорядочены включением

.

Проверим, будет ли это отношение частичным порядком. Заметим, что

.

Так как для всех , то отношение рефлексивно. Видно, что отношение не является симметричным. Но если и , то , иначе из следует . Следовательно, антисимметрично. Пусть и , т.е. и . Тогда и и, следовательно, или , а значит . Таким образом, транзитивно. Обобщая, сделаем вывод, что является отношением частичного порядка.