
Учебное пособие 1942
.pdf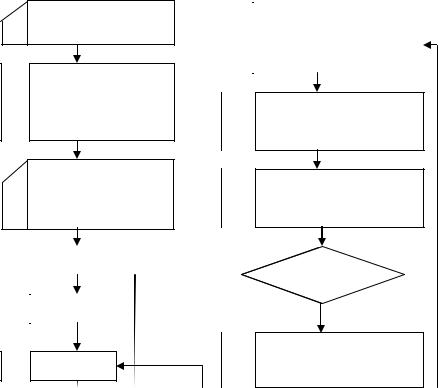
приемлемый вариант.
При использовании манипуляторов с большим количеством координат может возникнуть некоторое конечное или бесконечное число вариантов решения. В этом случае многовариантность решения обратной задачи можно использовать для оптимизации траектории движения по быстродействию или иному критерию /23/.
1 |
Ввод постоянных |
параметров l1, l2, m, E |
2Определение типов массивов, переменных и процедуры
STRAIGHT
9 |
Определение средне- |
|
квадратичного от- |
|
клонения U схвата от |
|
целевого состояния |
|
|
10Определение прира-
щений β1, β 2, β 3 угловых координат
|
Ввод исходных уг- |
|
Вычисление новых |
3 |
ловых координат β1, |
11 |
|
β 2, β 3 и массивов |
|
значений угловых |
|
|
|
||
|
X1C, X2C, X3C |
|
координат β1, β 2, β 3 |
4 |
t1= t10 |
|
|
|
|
|
|
|
|
|
12 |
|
34. |
||
|
|
|
|
|
|
||
|
|
|
|||||
|
|
|
|
|
|
|
|
5 |
j = 0 |
|
|
|
|
|
221 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 Проверка соответствия
6 j=j +1 ограничениям на обобщенные координаты
Рис. 6.8. Алгоритм решения обратной задачи кинематики Программа 1
implementation const PI=3.14159;
222
L1=500; L2=765; { длины звеньев манипулятора } m=3; { число опорных точек }
type arr=array[1..m] of real;
var X1T,X2T,X3T, {текущие декартовые координаты схвата и } DX1,DX2,DX3, { их отклонения от заданных } DB1,DB2,DB3, {требуемые приращения угловых координат}
S1,S2,S3,C1, |
{ синусы и косинусы в соответствии } |
C2,C3,S23, |
{ с угловыми координатами } |
U:real; |
{ среднеквадратичное отклонение } |
B1I,B2I,B3I, |
{исходные угловые координаты} |
B1,B2,B3: real; {массив рассчитанных угловых координат} X1C,X2C,X3C:arr; {массив заданных декартовых координат}
{$R *.DFM}
{Ввод исходных угловых и заданных декартовых координат} procedure TfmExample.Button1Click(Sender: TObject);
begin B1:=StrToFloat(Edit1.Text); B2:=StrToFloat(Edit2.Text); B3:=StrToFloat(Edit3.Text);
X1C[1]:=StrToFloat(Edit4.Text);
X2C[1]:=StrToFloat(Edit5.Text);
223
X3C[1]:=StrToFloat(Edit6.Text);
X1C[2]:=StrToFloat(Edit7.Text);
X2C[2]:=StrToFloat(Edit8.Text);
X3C[2]:=StrToFloat(Edit9.Text);
X1C[3]:=StrToFloat(Edit10.Text);
X2C[3]:=StrToFloat(Edit11.Text);
X3C[3]:=StrToFloat(Edit12.Text);
end;
{Процедура решения прямой задачи кинематики} procedure STRAIGHT(B1,B2,B3:real;var X1,X2,X3:real);
begin
S1:=sin(B1); { вычисление тригонометрических функций }
S2:=sin(B2);
S3:=sin(B3);
C1:=cos(B1);
C2:=cos(B2);
C3:=cos(B3); S23:=sin(B3-B2);
X1:=(L1*C2-L2*C3)*S1; { текущие декартовые координаты}
X2:=L1*S2-L2*S3; X3:=(L1*C2-L2*C3)*C1;
end; { конец процедуры STRAIGHT }
224
{Процедура решения обратной задачи кинематики} procedure TfmExample.Button3Click(Sender: TObject); LABEL 1,2,3,4;
var j:integer; begin
FOR j:=1 TO 3 DO begin
1: repeat STRAIGHT(B1I,B2I,B3I,X1T,X2T,X3T);
{ отклонения схвата от целевого положения }
DX1:=X1C[J]-X1T;
DX2:=X2C[J]-X2T;
DX3:=X3C[J]-X3T;
{среднеквадратичное отклонение схвата }
U:=SQRT(DX1*DX1+DX2*DX2+DX3*DX3);
{определение требуемых приращений угловых координат }
DB1:=(DX1*C1-DX3*S1)/(L1*C2-L2*C3);
DB2:=((DX1*S1+DX3*C1)*C3+DX2*S3)/(L1*S23);
DB3:=((DX1*S1+DX3*C1)*C2+DX2*S2)/(L2*S23);
{ вычисление новых значений угловых координат}
B1I:=B1I+DB1;
225
B2I:=B2I+DB2;
B3I:=B3I+DB3;
UNTIL U<10;
{ проверка требуемых ограничений на угловые координаты}
IF (B1I>0) AND (B1I<1.6) THEN GOTO 2 ELSE BEGIN
B1I:=1;
GOTO 1; END;
2:IF (B2I>0.7) AND (B2I<2.4) THEN GOTO 3 ELSE BEGIN
B2I:=1.5; GOTO 1; END;
3:IF (B3I>-0.8) AND (B3I<0.8) THEN GOTO 4 ELSE BEGIN
B3I:=0; GOTO 1;
END;
{ Вывод рассчитанных угловых координат }
4:case j of
1:begin
226
Edit1.text:=FloatToStr(B1I);
Edit2.text:=FloatToStr(B2I);
Edit3.text:=FloatToStr(B3I);
end;
2:begin Edit13.text:=FloatToStr(B1I); Edit14.text:=FloatToStr(B2I); Edit15.text:=FloatToStr(B3I); end;
3:begin Edit16.text:=FloatToStr(B1I); Edit17.text:=FloatToStr(B2I); Edit18.text:=FloatToStr(B3I); end;
end;
end;
6.5. Программная реализация алгоритма интерполяции
На практике для интерполяции траектории между опорными точками могут быть использованы полиномы различных порядков. Кубические полиномы обеспечивают непрерывность перемещений, скоростей и ускорений в опорных точках. Относительно низкая степень полино-
227
ма сокращает вычислительные затраты и снижает возможность возникновения неустойчивости при вычислениях, и в то же время управляющие сигналы являются достаточно плавными. Поэтому интерполяция траектории кубическими сплайнами часто используется при контурном управлении роботом.
Определим параметры сплайнов Pj , s 3 (t), s = 1, ... , m , из условий (3.34), (3.35), (3.36) и (3.38). Этот сплайн может быть представлен в следующем виде:
|
|
|
(t s -t)3 |
|
(t -ts - 1 )3 |
|
|
|
||||||
Pj , s 3 (t )= Mj , s - 1 |
|
|
+ Mj s |
|
|
|
|
+(qj , s - 1 - |
|
|||||
6 hj s |
|
6 hj s |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
hj s 2 t s -t |
|
hj s 2 t-t s - 1 |
|
||||||||||
-Mj , s - 1 |
|
) |
|
+(qj s -Mj s |
|
) |
|
|
|
, |
(6.8) |
|||
|
|
|
|
|
|
|||||||||
6 |
|
hj s |
6 |
|
hj s |
|
|
|
||||||
где j – номер обобщенной координаты; |
|
|
|
|||||||||||
s = 1, 2, ... , m – номер временного интервала; |
|
|||||||||||||
Mj , s - 1 , Mj s , |
– постоянные параметры для s-го интервала времени при движении по j-й ко- |
|||||||||||||
ординате; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hj s = t s -t s - 1 – длительность временного интервала с номером s; t - текущее время;
qj , s - 1 , qj s – значения обобщенной координаты j в начале и конце интервала времени
228
Сплайн, описываемый выражением (6.8), уже удовлетворяет условиям (3.34) и (3.36). При любых значениях Mj s его ускорения непрерывны и изменяются по кусочно-линейному закону
. . |
ts -t |
t -t s - 1 |
|
|
|||
|
|
|
|
|
Pj , s 3 (t )=Mj , s - 1 |
+ Mj s |
(6.9) |
|
|
|
|
||||
|
h j s |
|
h j s |
|
|
||
на отрезке времени [ts-1, ts].
Из уравнения (6.8) следуют выражения для определения скорости изменения обобщенной координаты на s-ом и s+1-м временных интервалах
. |
|
(t-ts-1)2 |
(ts-t)2 |
|
|
|
|
|
|
||||||||
Pj,s3(t) = Mjs |
|
|
|
|
|
- Mj,s-1 |
|
|
- |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2hjs |
|
2hjs |
|
|
|
|
|
|
|||||||
|
|
hjs |
2 |
|
1 |
|
|
|
|
hjs |
2 |
1 |
|
|
|||
-(qj,s-1- Mj,s-1 |
|
|
|
) |
|
|
|
+ (qjs - Mjs |
|
|
) |
|
, |
(6.10) |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
6 |
|
|
|
hjs |
|
|
|
6 |
|
|
hjs |
|
|||
. |
|
|
|
|
(t-ts)2 |
|
(ts+1-t)2 |
|
|
|
|||||||
Pj,s+1,3(t) = Mj,s+1 |
|
|
|
|
- Mjs |
|
|
|
- |
|
|
||||||
|
|
|
|
|
2hj,s+1 |
|
2hj,s+1 |
|
|
|
|||||||
hj,s+12 |
1 |
|
|
|
|
|
|
hj,s+12 1 |
|
||||||||
229

- (qjs - Mjs |
|
) |
|
+(qj,s+1-Mj,s+1 |
|
) |
|
, (6.11) |
|
|
|
|
|||||
6 |
|
hj,s+1 |
6 |
|
hj,s+1 |
|||
Условия непрерывности скоростей (3.35) позволяют получить из выражений (6.10), (6.11) следующее уравнение:
|
hjs |
|
|
|
hjs+ hj,s+1 |
|
hj,s+1 |
|
|||
Mj,s-1 6 |
+ Mjs |
|
+ Mj,s+1 |
|
|
= |
|||||
3 |
6 |
|
|||||||||
= |
qj,s+1 - qjs |
- |
|
qjs - qj,s-1 |
|
, |
s =1, ... , m-1. (6.12) |
||||
hj,s+1 |
|
|
hjs |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
Условия равенства нулю скорости входного сигнала в начале и в конце траектории (3.38) дают на основе системы уравнений (6.10), (6.11) следующие уравнения для определения пара-
метров Mj 0 |
, Mj 1 |
, ..., Mj m : |
|
|
|
|
||||
|
|
|
hj 1 |
hj 1 |
qj 1 - qj 0 |
|
||||
|
|
Mj 0 |
|
|
+ Mj 1 |
|
|
= |
|
, |
|
|
3 |
|
6 |
|
hj 1 |
||||
|
|
|
|
|
|
|
|
|
|
(6.13) |
|
Mj , m - 1hj m + Mj m |
hj m = qj , m - 1 -qj m . |
||||||||
|
|
|
6 |
|
|
|
3 |
hj m |
|
|
230
