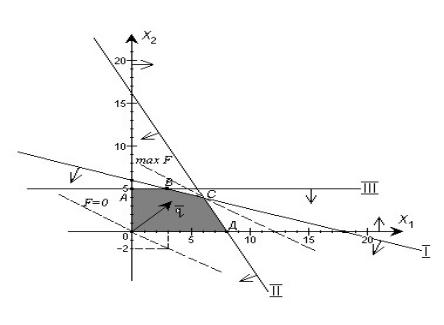
Рис. 1.

3. Нахождение решения задачи линейного программирования

Для решения ЗЛП существует универсальный метод– метод последовательного улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: сим- плекс-метода с естественным базисом и симплекс-метода с искусственным базисом(М- метод).

Выбор конкретной вычислительной процедуры осуществляется после приведения -ис ходной ЗЛП к каноническому виду.

Для применения симплекс-метода с естественным базисом ЗЛП должна содержать единичную подматрицу размером mxm – в этом случае очевиден начальный опорный план.

Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные записать в таблицу:

В первом столбце таблицы"Базис" записывают базисные векторы данного опорного плана. Во втором столбце - коэффициенты целевой функции (с1, с2,…, сm) при базисных переменных (напомним, что в базис входят только векторы, образующую единичную подматрицу). В третьем столбце Р0 - правая часть ограничений задачи (базисные компоненты плана). Таким образом, перемножая элементы второго столбца таблицы со столбцом Р0, и суммируя эти произведения, мы получаем значение целевой функции(F0=с1*b1 + с2*b2+…+

сm*bm).

Первая строка симплексной таблицы содержит коэффициенты целевой функции нашей задачи и остается неизменной на протяжении всего решения (с1, с2,…, сm).

В центральной части таблицы записывают коэффициенты при неизвестных в ограничениях исходной задачи. При этом следует заметить, что коэффициенты при базисных пере-

5

менных в ограничениях задачи составляют единичную подматрицу. Последнюю оценочную

m

строку рассчитывают по формуле D j = åci aij - c j .

i=1

После заполнения таблицы исходный опорный план проверяют на оптимальность. Для

матрицы коэффициентов мы вводим в исходную задачу неотрицательные так называемые искусственные переменные и включаем их в целевую функцию с коэффициентом+М для задачи минимизации и с коэффициентом-М для задачи максимизации, где М>0 - сколь угодно большое число. Полученная задача называется расширенной по отношению к исходной. Искусственные переменные образуют начальное базисное решение. Применив сим- плекс-метод, необходимо вывести из базиса все искусственные переменные. Если удается доказать (или показать), что искусственные переменные полностью вывести из базиса -не возможно, то это означает, что задача не имеет решения, то есть ее ограничения противоречивы.

Если на текущей итерации из базиса выводится искусственная переменная, то в следующей симплекс-таблице соответствующий ей столбец можно удалить, в дальнейших итерациях он не будет участвовать.

6

4.Двойственность в задачах линейного программирования

Скаждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной или прямой.

Две приведенные задачи образуют двойственную пару.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид "£", в задаче на минимум — вид "³";

2)матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи и аналогичная матрица Ат в двойственной задаче получаются друг из друга транспонированием;

3)число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи— числу переменных

висходной задаче;

4)коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограни-

чениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;

5) если переменная xj исходной задачи может принимать только положительные значения, то j-ое условие в системе ограничений двойственной задачи является неравенством вида "≥". Если же переменная может принимать как положительные, так и отрицательные значения, то j-ое условие представляет собой уравнение. И наоборот, если i-ое соотношение в системе ограничений исходной задачи является неравенством, то i-ая переменная двойственной задачи yi. В противном случае переменная yi может принимать как положительные, так и отрицательные значения.

7

В теории двойственности используются четыре пары двойственных задач (приведем их в

X ³ 0;

Первая теорема двойственности.

Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны меж-

ду собой, т. е. Fmax = gmin .

Если же целевая функция одной из пары двойственных задач не ограничена(для исходной – сверху, для двойственной – снизу), то другая задача вообще не имеет планов.

Вторая теорема двойственности.

План X * = (x1* , x2* ,..., xn* ) исходной задачи и план Y * = ( y1* , y2* ,..., yn* ) двойственной зада-

чи являются оптимальными планами этих задач тогда и только тогда, когда для любых i и j выполняются равенства:

Если в оптимальном плане одной из задач соответствующая переменная отлична от нуля, то ограничение другой задачи в оптимальном плане выполняются в виде равенства. Если в оптимальном плане одной из задач какое-либо ограничение выполняется в виде строгого неравенства, то соответствующая переменная другой задачи в оптимальном плане равна нулю.

Эти условия позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

8

Пример. Решить задачу линейного программирования симплексным методом. Составить для данной задачи линейного программирования двойственную задачу и по решению прямой задачи найти решение двойственной, используя теоремы двойственности.

Приведем задачу к каноническому виду. Для этого к левой часть первого неравенства прибавим дополнительную неотрицательную переменную x3 , к левой части второго - x4 . А

вот из левой части третьего неравенства вычтем переменную x5 . В целевую функцию каждая из этих переменных входит с коэффициентом 0 (т. е. не входят). Получаем

Преобразованную систему уравнений запишем в векторной форме: x1 P1 + x2 P2 + x3 P3 + x4 P4 + x5 P5 = P0 ,

Среди векторов P1, P2, P3, P4, P5, только два единичных вектора (P3 и P4), т.е. единичного базиса нет. Поэтому составим расширенную задачу. Для этого в левую часть третьего уравнения системы ограничений добавимискусственную переменную x6 . Её нужно как

можно быстрее вывести из базиса. Поэтому в целевую функцию в задаче максимизации новая переменная войдёт с очень большим отрицательным коэффициентом–М. Расширенная задача имеет опорный план X = (0, 0, 1, 8, 0, 3) , определяемый системой трёх единичных век-

торов: P3 , P4 , P6 .

Составим симплексную таблицу для I итерации:

с2, ...,сm):

m

z j = åci aij ( j = 1, m) .

i=1

9

D2 =Cб P2 - с2 = (0,0,-M ) × (2,1,1) - 3 = -3 - M;

D3 = Cб P3 - с3 = (0,0,-M ) × (1,0,0) - 0 = 0;

D4 =Cб P4 - с4 = (0,0,-M ) × (0,1,0) - 0 = 0;

D5 =Cб P5 - с5 = (0,0,-M ) × (0,0,-1) - 0 = M;

D6 =Cб P6 - с6 = (0,0,-M) ×(0,0,1) - (-M ) = 0.

Оценки векторов, входящих в базис, всегда равны нулю.

Значение F0 равно скалярному произведению вектораP0 на вектор Сб:

F0=1*0+8*0+3*(-М) = -3М.

Значения F0 и z j -c j состоят из двух слагаемыхMa j + b j . Слагаемое, которое не со-

держит М, записываем в 4-й строке, а число, стоящее при М – в 5-й.

Начальное опорное решение не является оптимальным, так как в 5-й строке имеется два отрицательных числа a1 = -2 и a2 = -1. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов. Чтобы перейти к новому опорному решению в базис можно ввести любой из векторов P1 и P2. Выберем P1, так как ему соответствует наибольшая по модулю оценка. Для определения вектора, подлежащего выво-

Минимум достигается при i=3. В третьей строке столбца «Базис» находится вектор Р6. Следовательно, его из базиса исключаем.

Далее выполним преобразование Жордана с разрешающим элементомa31 =2: 1) разде-

лим всю третью строку на2 и запишем результат в новую симплексную таблицу; 2) остальные элементы первого столбца нужно занулить, для этого полученную 3-ю строку сложим с первой, результат запишем в первую строку новой симплексной таблицы; 3) умножим 3-ю строку на -2 и сложим со второй строкой, результат запишем во вторую строку новой симплексной таблицы.

Получим симплексную таблицу для II итерации:

Она содержит только четыре строки, так как искусственный вектор из базиса исключён и оценки больше не содержат слагаемого с .МЭтот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора можно не заполнять. Но так как от нас требуется найти решение двойственно задачи, то мы его оставим.

Рассмотрим элементы 4-й строки. В столбце векторов P2 и P5 имеются отрицательные числа, значит, найденный план не является оптимальным. Вводить в базис будем вектор P2 , исключать P3 . Получим симплексную таблицу для III итерации.

10

Последняя строка снова содержит отрицательное число. В базис вводим вектор P5 , ис-

ключаем P4 .

В 4-й строке последней симплексной таблицы нет отрицательных чисел. Значит найденный опорный план X * = (3, 2, 0, 0, 5, 0) является оптимальным. Значение целевой функции zmax = 12 .

Составим двойственную задачу.

Умножим третье ограничение на-1, тогда все неравенства будут содержать знак«≤». Задача примет вид исходной задачи симметричной пары 1:

x1 , x2 ³ 0.

Число переменных в двойственной задаче равно числу ограничений в исходной задаче, т.е. трём: y1 , y2 , y3 .

Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию: g = y1 + 8y2 - 3y3 .

Целевая функция исходной задачи исследуется на максимум, следовательно, целевая функция двойственной задачи исследуется на минимум.

11

Окончательно двойственная задача имеет следующий вид:

Найдём её решение, используя теоремы двойственности. По первой теореме двойст-

Из соотношений второй теоремы двойственности следует, что если какое-то ограничение исходной задачи выполняется в виде строгого неравенства, то соответствующая двойственная оценка равна нулю. Подставим найденное оптимальное решение в систему ограничений исходной задачи:

-1* 3 + 2 * 2 = 1 = 1, 2 * 3 +1* 2 = 8 = 8, 2 * 3 +1* 2 = 7 > 3.

Третье ограничение выполняется в виде строгого неравенства, следовательно, y3* = 0 .

Если некоторая компонента xi* оптимального плана исходной задачи отлична от нуля, то соответствующее ограничение двойственной задачи выполняется в виде равенства. В нашем примере и x1* = 3 ¹ 0 , и x2* = 2 ¹ 0 , следовательно, оба ограничения двойственной задачи выполняются в виде равенства.

Решив систему, получим y1 = 4 / 5, y2 = 7 / 5.

Окончательно Y * = (4 / 5, 7 / 5, 0), g min = 12.

Решение двойственной задачи можно получить другим способом, используя формулу

Y * = CБ P-1 .

Матрица P-1 находится в последней симплексной таблице. Ее столбцы расположены под столбцами единичной матрицы, образующими базис начального опорного решения, т. е. под векторами P3 , P4 , P6 (именно для этой цели мы продолжали вычислять вектор P6 ):

12